当前位置:网站首页>设f(x)=∑x^n/n^2,证明f(x)+f(1-x)+lnxln(1-x)=∑1/n^2
设f(x)=∑x^n/n^2,证明f(x)+f(1-x)+lnxln(1-x)=∑1/n^2
2022-07-06 23:18:00 【深海里的鱼(・ω<)*】
题目
设 f ( x ) = ∑ n = 1 ∞ x n n 2 ,证明: f ( x ) + f ( 1 − x ) + ln x ln ( 1 − x ) = ∑ n = 1 ∞ 1 n 2 \text{设}f\left( x \right) =\sum_{n=1}^{\infty}{\frac{x^n}{n^2}}\text{,证明:}f\left( x \right) +f\left( 1-x \right) +\ln x\ln \left( 1-x \right) =\sum_{n=1}^{\infty}{\frac{1}{n^2}} 设f(x)=n=1∑∞n2xn,证明:f(x)+f(1−x)+lnxln(1−x)=n=1∑∞n21
解答
f ′ ( x ) = ∑ n = 1 ∞ x n − 1 n = 1 x ∑ n = 1 ∞ x n n = 1 x ∫ 0 x ∑ n = 1 ∞ t n − 1 d t = 1 x ∫ 0 x ∑ n = 0 ∞ t n d t = 1 x ∫ 0 x 1 1 − t d t = − ln ( 1 − x ) x f'\left( x \right) =\sum_{n=1}^{\infty}{\frac{x^{n-1}}{n}}=\frac{1}{x}\sum_{n=1}^{\infty}{\frac{x^n}{n}}=\frac{1}{x}\int_0^x{\sum_{n=1}^{\infty}{t^{n-1}}dt}=\frac{1}{x}\int_0^x{\sum_{n=0}^{\infty}{t^n}dt}=\frac{1}{x}\int_0^x{\frac{1}{1-t}dt}=-\frac{\ln \left( 1-x \right)}{x} f′(x)=n=1∑∞nxn−1=x1n=1∑∞nxn=x1∫0xn=1∑∞tn−1dt=x1∫0xn=0∑∞tndt=x1∫0x1−t1dt=−xln(1−x)
f ′ ( x ) − f ′ ( 1 − x ) = − ln ( 1 − x ) x + ln x 1 − x f'\left( x \right) -f'\left( 1-x \right) =-\frac{\ln \left( 1-x \right)}{x}+\frac{\ln x}{1-x} f′(x)−f′(1−x)=−xln(1−x)+1−xlnx
∵ [ ln x ln ( 1 − x ) ] ′ = ln ( 1 − x ) x − ln x 1 − x \because \left[ \ln x\ln \left( 1-x \right) \right] '=\frac{\ln \left( 1-x \right)}{x}-\frac{\ln x}{1-x} ∵[lnxln(1−x)]′=xln(1−x)−1−xlnx
∴ f ′ ( x ) − f ′ ( 1 − x ) + [ ln x ln ( 1 − x ) ] ′ = 0 \therefore f'\left( x \right) -f'\left( 1-x \right) +\left[ \ln x\ln \left( 1-x \right) \right] '=0 ∴f′(x)−f′(1−x)+[lnxln(1−x)]′=0
令 g ( x ) = f ( x ) + f ( 1 − x ) + ln x ln ( 1 − x ) x ∈ ( 0 , 1 ) \text{令}g\left( x \right) =f\left( x \right) +f\left( 1-x \right) +\ln x\ln \left( 1-x \right) \ \ x\in \left( 0,1 \right) 令g(x)=f(x)+f(1−x)+lnxln(1−x) x∈(0,1)
∴ g ′ ( x ) = 0 \therefore g'\left( x \right) =0 ∴g′(x)=0
∵ ∫ 0 x g ′ ( u ) d u = g ( x ) − lim t → 0 + g ( t ) = 0 \because \int_0^x{g'\left( u \right)}du=g\left( x \right) -\underset{t\rightarrow 0^+}{\lim}g\left( t \right) =0 ∵∫0xg′(u)du=g(x)−t→0+limg(t)=0
∴ g ( x ) = lim t → 0 + g ( t ) \therefore g\left( x \right) =\underset{t\rightarrow 0^+}{\lim}g\left( t \right) ∴g(x)=t→0+limg(t)
∵ lim t → 0 + g ( t ) = lim t → 0 + f ( t ) + lim t → 0 + f ( 1 − t ) + lim t → 0 + ln t ⋅ ln ( 1 − t ) \because \underset{t\rightarrow 0^+}{\lim}g\left( t \right) =\underset{t\rightarrow 0^+}{\lim}f\left( t \right) +\underset{t\rightarrow 0^+}{\lim}f\left( 1-t \right) +\underset{t\rightarrow 0^+}{\lim}\ln t\cdot \ln \left( 1-t \right) ∵t→0+limg(t)=t→0+limf(t)+t→0+limf(1−t)+t→0+limlnt⋅ln(1−t)
其中 lim t → 0 + f ( t ) = 0 , lim t → 0 + f ( 1 − t ) = ∑ n = 1 ∞ 1 n 2 , lim t → 0 + ln t ⋅ ln ( 1 − t ) = lim t → 0 + t ln t = lim t → 0 + ln t 1 t = lim t → 0 + 1 t − 1 t 2 = 0 \text{其中}\underset{t\rightarrow 0^+}{\lim}f\left( t \right) =0,\ \underset{t\rightarrow 0^+}{\lim}f\left( 1-t \right) =\sum_{n=1}^{\infty}{\frac{1}{n^2}},\ \underset{t\rightarrow 0^+}{\lim}\ln t\cdot \ln \left( 1-t \right) =\underset{t\rightarrow 0^+}{\lim}t\ln t=\underset{t\rightarrow 0^+}{\lim}\frac{\ln t}{\frac{1}{t}}=\underset{t\rightarrow 0^+}{\lim}\frac{\frac{1}{t}}{-\frac{1}{t^2}}=0 其中t→0+limf(t)=0, t→0+limf(1−t)=n=1∑∞n21, t→0+limlnt⋅ln(1−t)=t→0+limtlnt=t→0+limt1lnt=t→0+lim−t21t1=0
∴ lim t → 0 + g ( t ) = ∑ n = 1 ∞ 1 n 2 \therefore \underset{t\rightarrow 0^+}{\lim}g\left( t \right) =\sum_{n=1}^{\infty}{\frac{1}{n^2}} ∴t→0+limg(t)=n=1∑∞n21
∴ g ( x ) = ∑ n = 1 ∞ 1 n 2 \therefore g\left( x \right) =\sum_{n=1}^{\infty}{\frac{1}{n^2}} ∴g(x)=n=1∑∞n21
∴ f ( x ) + f ( 1 − x ) + ln x ln ( 1 − x ) = ∑ n = 1 ∞ 1 n 2 \therefore f\left( x \right) +f\left( 1-x \right) +\ln x\ln \left( 1-x \right) =\sum_{n=1}^{\infty}{\frac{1}{n^2}} ∴f(x)+f(1−x)+lnxln(1−x)=n=1∑∞n21
边栏推荐
- 腾讯云数据库公有云市场稳居TOP 2!
- [736. LISP syntax parsing]
- 2039: [Bluebridge cup 2022 preliminaries] Li Bai's enhanced version (dynamic planning)
- Inventory host list in ansible (I wish you countless flowers and romance)
- U++ 元数据说明符 学习笔记
- 在米家、欧瑞博、苹果HomeKit趋势下,智汀如何从中脱颖而出?
- 磁盘监控相关命令
- 基于Bevy游戏引擎和FPGA的双人游戏
- window定时计划任务
- The execution order of return in JS' try catch finally
猜你喜欢
If you‘re running pod install manually, make sure flutter pub get is executed first.
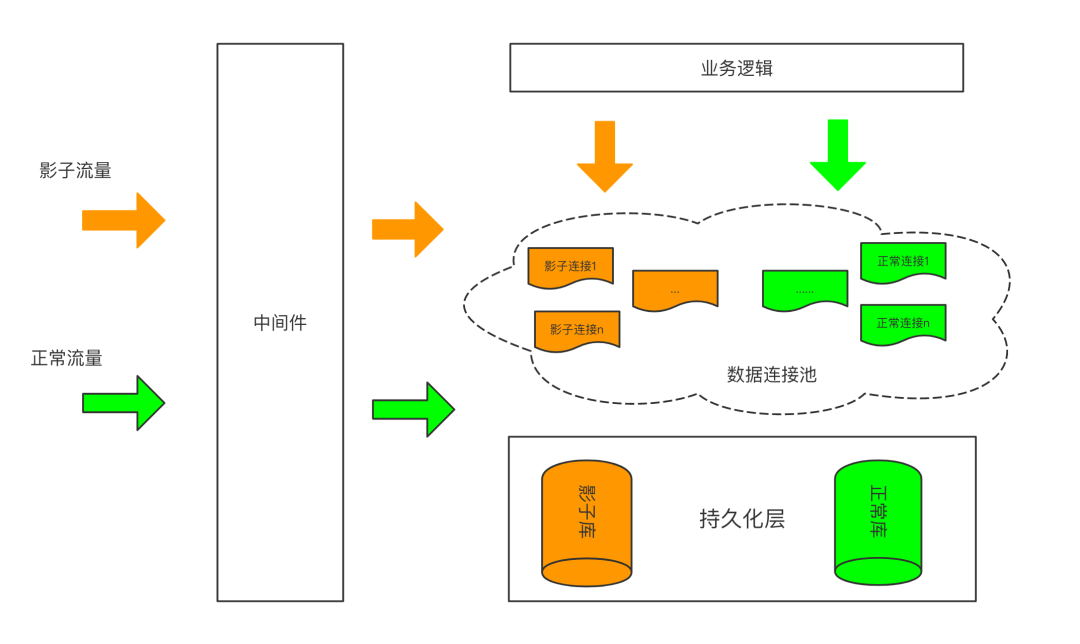
Full link voltage test: the dispute between shadow database and shadow table
Error: No named parameter with the name ‘foregroundColor‘
U++4 interface learning notes
基于Bevy游戏引擎和FPGA的双人游戏
![[736. LISP syntax parsing]](/img/62/5e2aeec150096aa3fd81025d146255.png)
[736. LISP syntax parsing]
Operand of null-aware operation ‘!‘ has type ‘SchedulerBinding‘ which excludes null.
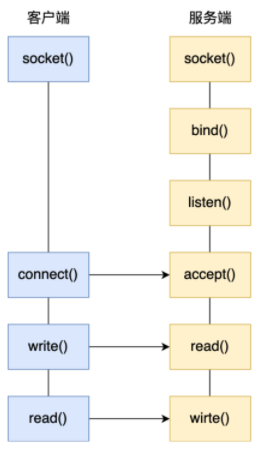
一文搞懂常见的网络I/O模型
Flask project uses flask socketio exception: typeerror: function() argument 1 must be code, not str
![[question] Compilation Principle](/img/ce/71f8409ba2cebd497bed0210290895.png)
[question] Compilation Principle
随机推荐
Techniques d'utilisation de sublime
NiO related knowledge points (I)
2. Overview of securities investment funds
Understand common network i/o models
If you‘re running pod install manually, make sure flutter pub get is executed first.
[question] Compilation Principle
Addressable 预下载
Linkedblockingqueue source code analysis - initialization
Operand of null-aware operation ‘!‘ has type ‘SchedulerBinding‘ which excludes null.
Y58. Chapter III kubernetes from entry to proficiency - continuous integration and deployment (Sany)
Knapsack problem unrelated to profit (depth first search)
pytest测试框架——数据驱动
Servicemesh mainly solves three pain points
Mysql database (basic)
Harmonyos fourth training
Ansible报错:“msg“: “Invalid/incorrect password: Permission denied, please try again.“
SQL injection HTTP header injection
HarmonyOS第四次培训
The founder has a debt of 1billion. Let's start the class. Is it about to "end the class"?
QT simple layout box model with spring