矩阵分解与梯度下降

目录

1、矩阵分解（矩阵乘法回顾）

2、梯度下降

3、矩阵算法推导

4、python代码实现

---

1、矩阵分解

①为何学习矩阵分解

矩阵算法就是将用户和产品矩阵中的数据，分解成两个矩阵（用User矩阵和Item矩阵），两个矩阵相乘得到的结果就是预测评分。 

矩阵分解就是把原来的大矩阵，近似的分解成小矩阵的乘积，在实际推荐计算时不再使用大矩阵，而是使用分解得到的两个小矩阵

具体来说就是，假设用户物品的评分矩阵A是m乘n维，即一共有m个用户，n个物品.通过一套算法转化为两个矩阵U和V,矩阵U的维度是m乘k，矩阵V的维度是n乘k。

就如同我们现在需要学习的推荐系统，这里面有缺失得评分，我们需要通过矩阵分解，算出这个缺失得评分

 我们的目的就是运用已知得评分来算出未知的评分

②回顾矩阵乘法

   大写字母表示矩阵，小写字母表示具体的值

   矩阵乘法有条件是第一个矩阵的列与第二个矩阵的行数相等

   

---

2、梯度下降 

梯度下降通俗解释：如同一个人想要下山，不知道怎么下山。于是决定走一步算一步，也就是每次沿着当前位置最陡峭最易下山的方向前进一小步，然后继续沿下一个位置最陡方向前进一小步。这样一步一步走下去，一直走到觉得我们已经到了山脚

 

 

通俗理解是首先带入初始位置，然后算出该点的导数，带入一步一步修改新的位置，再进行迭代，直到斜率小于等于参数。相当于找到了最小值 

 

---

 3、矩阵算法推导

       

使用梯度下降方法获得修正的p和q分量： 

根据负梯度的方向更新变量： 

最后再不停迭代直到算法最终收敛 

---

3、python代码

import numpy as np
import math
import matplotlib.pyplot as plt



# 定义矩阵分解函数
def Matrix_decomposition(R, P, Q, N, M, K, alpha=0.0002, beta=0.02):
    Q = Q.T  # Q 矩阵转置
    loss_list = []  # 存储每次迭代计算的 loss 值
    for step in range(5000):
        # 更新 R^
        for i in range(N):
            for j in range(M):
                if R[i][j] != 0:
                    # 计算损失函数
                    error = R[i][j]
                    for k in range(K):
                        error -= P[i][k] * Q[k][j]
                    # 优化 P,Q 矩阵的元素
                    for k in range(K):
                        P[i][k] = P[i][k] + alpha * (2 * error * Q[k][j] - beta * P[i][k])
                        Q[k][j] = Q[k][j] + alpha * (2 * error * P[i][k] - beta * Q[k][j])

        loss = 0.0
        # 计算每一次迭代后的 loss 大小，就是原来 R 矩阵里面每个非缺失值跟预测值的平方损失
        for i in range(N):
            for j in range(M):
                if R[i][j] != 0:
                    # 计算 loss 公式加号的左边
                    data = 0
                    for k in range(K):
                        data = data + P[i][k] * Q[k][j]
                    loss = loss + math.pow(R[i][j] - data, 2)
                    # 得到完整 loss 值
                    for k in range(K):
                        loss = loss + beta / 2 * (P[i][k] * P[i][k] + Q[k][j] * Q[k][j])
                    loss_list.append(loss)
        plt.scatter(step, loss)
        # 输出 loss 值
        if (step + 1) % 1000 == 0:
            print("loss={:}".format(loss))
        # 判断
        if loss < 0.001:
            print(loss)
            break
    plt.show()
    return P, Q


if __name__ == "__main__":
    N = 5
    M = 4
    K = 5
    R = np.array([[5, 3, 0, 1],
                  [4, 0, 0, 1],
                  [1, 1, 0, 5],
                  [1, 0, 0, 4],
                  [0, 1, 5, 4]])  # N=5,M=4
    print("初始评分矩阵：")
    print(R)
    # 定义 P 和 Q 矩阵
    P = np.random.rand(N, K)  # N=5,K=2
    Q = np.random.rand(M, K)  # M=4,K=2

    print("开始矩阵分解：")
    P, Q = Matrix_decomposition(R, P, Q, N, M, K)
    print("矩阵分解结束。")
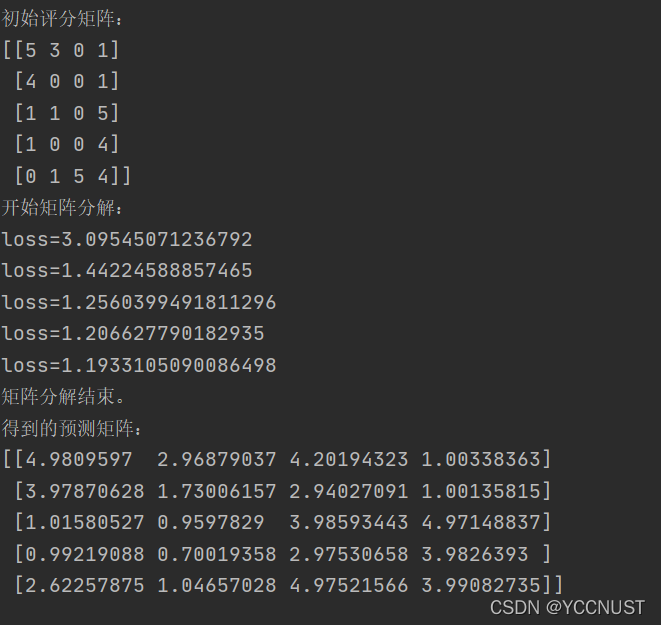
    print("得到的预测矩阵：")
    print(np.dot(P, Q))

结果输出