浮点数基础知识

在开发中过程中，经常会遇到比较两个浮点数大小的问题。 根据业务需求，可能会有如下比较方式：

float a = 0.2323f;
float b = 0.2324343f;

if (a - b < 1e-2) {
    
	// 若 a b之差在一个很小范围内，则可认为二者相等。 
}

为什么要这么比较呢？因为一个计算机的“常识” ，即浮点数的表示不是精确的，而是近似的。

如下代码，将100个0.1相加，得到的结果并不刚好是10，而是 10.000002。

fun main() {
    
	var sum = 0.0f
    for (i in 1 .. 100) {
    
        sum += 0.1f
    }
    
    println("sum is $sum")
}

// 这是一段用kotlin写的演示代码，运行结果如下：
sum is 10.000002

那么，浮点数为什么不能精确的表示呢？

首先，我们从十进制入手，将0.111111各位位权展开如下

0	.	1	1	1	1	1	1
0 * 10^0	.	1 * 10^-1	1 * 10^-2	1 * 10^-3	1 * 10^-4	1 * 10^-5	1 * 10^-6

可以看到，小数即对应位权指数为负数。拓展到二进制，也可如此表示，以两位小数为例。

0	.	0	1
0 * 2^0	.	0 * 2^-1	1 * 2^-2	对应十进制：0.25
0	.	1	0
0 * 2^0	.	1* 2^-1	0 * 2^-2	对应十进制：0.5
0	.	1	1
0 * 2^0	.	1* 2^-1	1* 2^-2	对应十进制：0.75

可以看到，在二进制中连续的三个小数，0.01，0.10，0.11 转化成对应的十进制数后并不是连续的，中间差了很多。 如0.25到0.5，中间少了0.26，0.27，0.28 … 0.49 。

如果我们将小数在扩大两位，看看4位小数的二进制表示的范围有多大。

个位	小数点	第一位	第二位	第三位	第四位	对应十进制值
0	.	0	0	0	1	0.0625
0	.	0	0	1	0	0.125
0	.	0	0	1	1	0.1875
0	.	0	1	0	0	0.25
0	.	0	1	0	1	0.3125
0	.	0	1	1	0	0.375
0	.	0	1	1	1	0.4375
0	.	1	0	0	0	0.5
0	.	1	0	0	1	0.5625
0	.	1	0	1	0	0.625
0	.	1	0	1	1	0.6875
0	.	1	1	0	0	0.75
0	.	1	1	0	1	0.8125
0	.	1	1	1	0	0.875
0	.	1	1	1	1	0.9375

我们仍然看到，即使扩大位数，用二进制表示的小数也不能完全表示连续的十进制数。当位数不断扩大时，也只能表示更多的十进制浮点数，但也还是无法精确的表示对应的十进制浮点数。

故二进制表示的浮点数无法精确的转化成对应的十进制数，这是浮点数无法精确计算的根本原因。

只能通过位数更长的二进制数来无限接近十进制表示的浮点数。

在计算机中，为了更好表示浮点数，避免了上面这种直接的表示方法。 而是采取了使用符号、尾数、基数、指数四部分来表示小数的方法。这四部分的说明如下：

这个结构类似科学计数法。 但是在计算机中还有一些额外的规定来实现浮点数的存储。

在java中，浮点数分为单精度浮点数和双精度浮点数，它们有什么区别的呢？单精度的存储位数位32位，而双精度存储位数为64位。如何用这些位来存储浮点数的四个部分呢？

如下图分别为32位和64位浮点数的存储格式

对于符号位很好理解，只需一位即可，0表示正数，1表示负数。 和补码规则中的表示正负是一样的。

尾数部分则规定，将小数点前面的数固定为1，同时仅保留小数位的数字。 具体的推算过程过下，摘自《程序是怎样跑起来的》

注意，这里移动并不考虑符号位，因为符号位是用单独的一位来存储。 最终得到的23位即为对应的浮点数的尾数部分。

对于指数部分，采用的是excess系统表示方法，具体参考百度百科。 如下摘取部分定义

Excess系统是计算机中可以同时存储正数和负数的一种方法。

以32位浮点数为例，8为指数可以表示的范围为0到255，但是为了表示负数，需要将其中的一半划归负数。最大值255（1111-1111）的一半为127（0111-1111，舍弃了小数部分，可以用二进制位移的算法来考虑，即为127）

然后用0到127的这部分表示-127到0的，用128到255表示1到128。此时就避免了使用补码来表示负数了。

具体的对应关系如下表

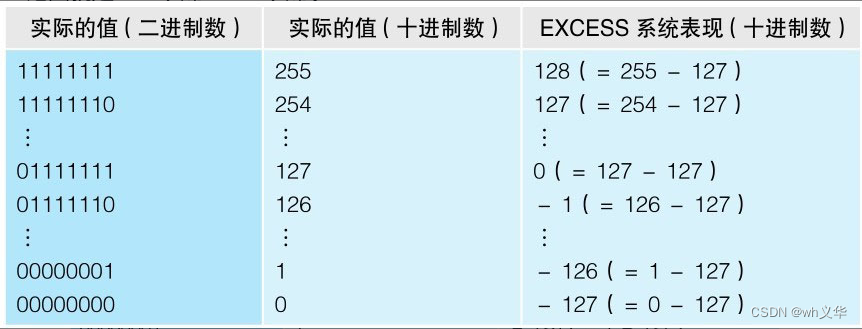
有了如上的规则，尝试使用规则将0.75换算为对应的二级制。

由于是正数，故符号位为0。

0.75用二进制表示为0.1100，为了将首位变为1，于是右移一位为1.100，然后将小数部分填充至23位，为10000000000000000000000。

由于尾数部分右移了一位，故指数应为-1。采用excess系统表示法，即为126，对应的二进制为 0111-1110.

综上，浮点数0.75在计算机中的表示为0-01111110-10000000000000000000000

采用书中的代码来校验一下，代码如下：

int main(void) {
    
    float data;
    unsigned long buff;
    char s[34];

    data = (float) 0.75;
    memcpy(&buff, &data, 4);
    
    for (int i = 33; i >= 0; i--) {
    
        if (i == 1 || i == 10) {
    
            s[i] = '-';
        } else {
    
            if (buff % 2 == 1) {
    
                s[i] = '1';
            } else {
    
                s[i] = '0';
            }
            buff /= 2;
        }
    }
    s[34] = '\0';
    printf("%s\n", s);

    return 0;
}

输出结果为：

0-01111110-10000000000000000000000

与推算的过程正好相符。 至此，就理解了浮点数在计算机中的存储方式。