论文信息
论文标题:Representation Learning on Graphs with Jumping Knowledge Networks
论文作者:Keyulu Xu, Chengtao Li, Yonglong Tian, Tomohiro Sonobe, Ken-ichi Kawarabayashi, Stefanie Jegelka
论文来源:2018,ICML
论文地址:download
论文代码:download
1 Introduction
最近,Figure said learning was proposed based on “邻域聚合” 一系列算法,This algorithm is heavily dependent on the graph structure,This paper proposes a flexible applications of different neighborhood structure jumping knowledge (JK) networks.
此外,将 JK framework 与 GCN 、GraphSAGE 和GAT 等模型相结合,Can continue to improve the performance of these models.
2 Model analysis
In addition to figure attribute information is very important,Graph structure of “邻域聚合” Algorithm is also very important.
In the same figure,If starting point is different,random walk The influence of the same steps after also is different,random walk How many step corresponding is the convolution of the iteration times.
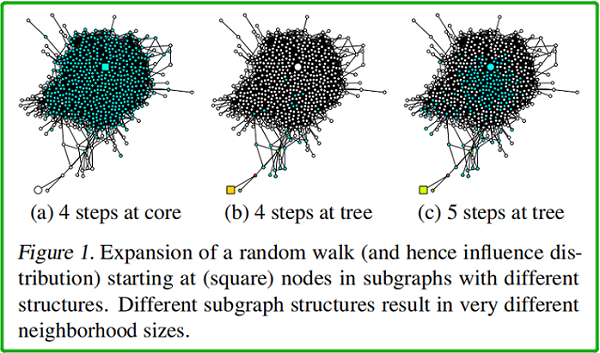
如上图所示,(a)、(b)、(c) 中 均以 square node 为起点.(a)中 square node Appear in the center populated place [core];(b)In the edges in the graph【此时的 random walk Path is similar to the tree structure】;(c) 在 (b) 的基础上, random walk The end point is located in the center populated place.
$\begin{array}{l}h_{\mathcal{N}(i)}^{(l+1)}=\operatorname{aggregate}\left(\left\{h_{j}^{l}, \forall j \in \mathcal{N}(i)\right\}\right) \\h_{i}^{(l+1)}=\sigma\left(W \cdot \operatorname{concat}\left(h_{i}^{l}, h_{\mathcal{N}(i)}^{l+1}\right)\right)\end{array}$
→ Whether can adaptively adjust(即学习)Each node of the affected radius?【可能 要减少 所谓 “邻域” 的大小】
→为实现这一点,This article explores a kind of learning to selectively use from different “邻域” The information architecture,将表示“跳转”到最后一层.
3 Related work
3.1 neighborhood aggregation scheme
Typical neighborhood aggregation scheme is as follows:
$h_{v}^{(l)}=\sigma\left(W_{l} \cdot \operatorname{AGGREGATE}\left(\left\{h_{u}^{(l-1)}, \forall u \in \tilde{N}(v)\right\}\right)\right) \quad\quad\quad(1)$
3.2 Graph Convolutional Networks (GCN)
Recall
two-layer GCN :
$Z=f(X, A)=\operatorname{softmax}\left(\hat{A} \operatorname{ReLU}\left(\hat{A} X W^{(0)}\right) W^{(1)}\right)$
其中,$\hat{A}=\tilde{D}^{-\frac{1}{2}} \tilde{A} \tilde{D}^{-\frac{1}{2}}$
Kipf 提出的 GCN:
其中,$c_{j i}=\sqrt{|\mathcal{N}(j)|} \sqrt{|\mathcal{N}(i)|}$
$h_{v}^{(l)}=\operatorname{ReLU}\left(W_{l} \cdot \frac{1}{\widetilde{\operatorname{deg}(v)}} \sum\limits _{u \in \widetilde{N}(v)} h_{u}^{(l-1)}\right)$
显然就是,$\hat{A}=\tilde{D}^{-1} \tilde{A} \quad\quad\quad(3)$
GCN 的 inductive 变形:
$\mathbf{h}_{\mathrm{v}}^{\mathrm{k}} \leftarrow \sigma\left(\mathbf{W} \cdot \operatorname{MEAN}\left(\left\{\mathbf{h}_{\mathrm{v}}^{\mathrm{k}-1}\right\} \cup\left\{\mathbf{h}_{\mathrm{u}}^{\mathrm{k}-1}, \forall \mathrm{u} \in \mathcal{N}(\mathrm{v})\right\}\right)\right)$
3.3 Neighborhood Aggregation with Skip Connections
$\begin{aligned}h_{N(v)}^{(l)} &=\sigma\left(W_{l} \cdot \operatorname{AGGREGATE}_{N}\left(\left\{h_{u}^{(l-1)}, \forall u \in N(v)\right\}\right)\right) \\h_{v}^{(l)} &=\operatorname{COMBINE}\left(h_{v}^{(l-1)}, h_{N(v)}^{(l)}\right)\end{aligned} \quad\quad\quad(4)$
COMBINE Step is the key to the paradigm of,Between different layers can be seen as a“skip connection”的一种形式.
GraphSAGE 的 Mean aggregator 形式:
$\begin{array}{l}\mathbf{h}_{\mathrm{v}}^{\mathrm{k}} \leftarrow \sigma\left(\mathbf{W} \cdot \operatorname{MEAN}\left(\left\{\mathbf{h}_{\mathrm{v}}^{\mathrm{k}-1}\right\} \cup\left\{\mathbf{h}_{\mathrm{u}}^{\mathrm{k}-1}, \forall \mathrm{u} \in \mathcal{N}(\mathrm{v})\right\}\right)\right. \\\mathbf{h}_{\mathrm{v}}^{\mathrm{k}} \leftarrow \sigma\left(\mathbf{W}^{\mathrm{k}} \cdot \operatorname{CONCAT}\left(\mathbf{h}_{\mathrm{v}}^{\mathrm{k}-1}, \mathbf{h}_{\mathcal{N}(\mathrm{v})}^{\mathrm{k}}\right)\right)\end{array}$
3.4 Neighborhood Aggregation with Directional Biases
GAT、VAIN、 GraphSAGE 中的 max-pooling operation Change the direction of the expansion,While in this paper, the model of effect on the expansion of local.
在第6节中,We have demonstrated our framework applies not only to simple neighborhood aggregation model(GCN),And also applies to skip links(GraphSAGE)和 带 directional biase 的 GAT .
4 Influence Distribution and Random Walks
受 sensitivity analysis 和 influence functions 的启发,We studied the characteristics of the scope of influence of a given node node,This range can obtain information given node neighborhood how much.
This paper measured the node $x$ 对节点 $y$ 的敏感性,或者 $y$ 对 $x$ 的影响,通过测量 $y$ Input characteristics of the change on the last layer $x$ The influence degree of the said.对于任何节点 $x$,influence distribution Captures the relative influence of all other nodes.
Definition 3.1 (Influence score and distribution). For a simple graph $G=(V, E)$ , let $h_{x}^{(0)}$ be the input feature and $h_{x}^{(k)}$ be the learned hidden feature of node $x \in V$ at the $k-th$ (last) layer of the model. The influence score $I(x, y)$ of node $x$ by any node $y \in V$ is the sum of the absolute values of the entries of the Jacobian matrix $\left[\frac{\partial h_{x}^{(k)}}{\partial h_{y}^{(0)}}\right]$ . We define the influence distribution $I_{x}$ of $x \in V$ by normalizing the influence scores: $I_{x}(y)=I(x, y) / \sum_{z} I(x, z)$ , or
$I_{x}(y)=e^{T}\left[\frac{\partial h_{x}^{(k)}}{\partial h_{y}^{(0)}}\right] e /\left(\sum\limits _{z \in V} e^{T}\left[\frac{\partial h_{x}^{(k)}}{\partial h_{z}^{(0)}}\right] e\right)$
where $e$ is the all-ones vector.
对于 completeness ,我们还定义了 random walk distributions :
Definition 3.2. Consider a random walk on $\widetilde{G}$ starting at a node $v_{0}$ ; if at the $t-th$ step we are at a node $v_{t}$ , we move to any neighbor of $v_{t}$ (including $v_{t}$ ) with equal probability.The $t$-step random walk distribution $P_{t}$ of $v_{0}$ is
$P_{t}(i)=\operatorname{Prob}\left(v_{t}=i\right) $
An important property is the distribution of the random walk,当 $t$ The increase in the,It has become more spread,If the figure is two of the department of,It converges to limit distribution.Convergence speed depends on the structure of the subgraph,And can be restricted by random walk transition matrix spectral gap.
4.1 Model Analysis
The following results show,The influence of public polymerization solution distribution is closely related to the distribution of random walk.This observation suggests that we will discuss the specific meaning of the——优势和缺点.
与 ReLU Activation of randomization assume similar,我们可以绘制GCNsAnd the connection between the random walk:
Theorem 1. Given a $k$-layer G C N with averaging as in Equation (3), assume that all paths in the computation graph of the model are activated with the same probability of success $\rho$ . Then the influence distribution $I_{x}$ for any node $x \in V$ is equivalent, in expectation, to the $k$-step random walk distribution on $\widetilde{G}$ starting at node $x$ .
证明如下:

通过修改 Theorem 1 的证明,可以直接证明 $\text{Eq.2}$ 中 GCN The results of the versions of an almost equivalent.
The only difference is that each slave node $x\left(v_{p}^{0}\right)$ 到 $y\left(v_{p}^{k}\right)$ Random walk path $v_{p}^{0}, v_{p}^{1}, \ldots, v_{p}^{k}$ Probability is not $\rho \prod_{l=1}^{k} \frac{1}{\overline{\operatorname{deg}\left(v_{p}^{l}\right)}}$ ,而是 $\frac{\rho}{Q} \prod_{l=1}^{k-1} \frac{1}{\widetilde{\operatorname{deg}\left(v_{p}^{l}\right)}} \cdot(\widetilde{\operatorname{deg}}(x) \widetilde{\operatorname{deg}}(y))^{-1 / 2}$,其中 $Q$ 是归一化因数.因此,The differences of probability is very small,特别是当 $x$ 和 $y$ When the degree of close.
同样地,We can prove directional deviation of neighborhood gathered scheme similar to the distribution of biased random walk.Then match the probability of substitution theorem1的证明中.
根据经验,我们观察到,Although some simplified assumptions,Our theory is close to what happened in practice.We will be trainedgcn的一个节点(Marked as square)The influence of the distribution of the heat map visualization,And from the same node began to compare the distribution of random walk with.Figure 2 Shows the example results.
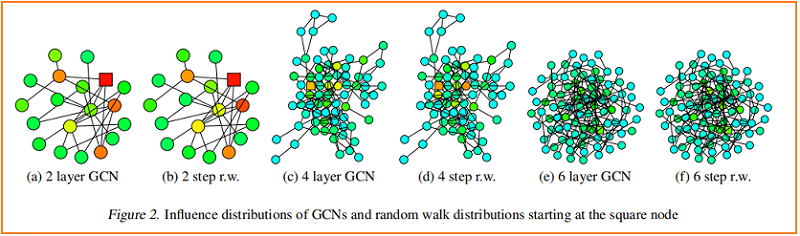
The darker color corresponds to the high impact probability.In order to show the skip connection effect,Figure 3 Visualize a similar heat map——具有 residual connections 的 GCN.事实上,我们观察到,With the influence of residual connection network distributed approximation corresponds to an inert random walk:Every step has higher probability to stay on the current node.在每次迭代中,The probability of all nodes in a similar retain partial information;It can not adapt to the different needs of specific upper nodes.
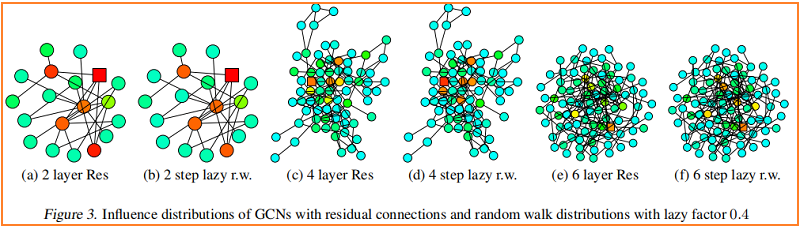
Fast Collapse on Expanders
Starting from the center of figure of random walk in $O(\log |V|)$ Step quickly converge to a nearly uniform distribution of.In the neighborhood of polymerization $O(\log |V|)$ 迭代之后,通过 Theorem 1,Each node of the said almost under the influence of figure within any other node.因此,Node said will represent global figure,And they carry a limited information on a single node.相比之下,从 bounded tree-width Some began to slow convergence of random walk with,That these characteristics retained more local information.Fixed on the distribution of the random walk model inherited the extension speed differences,And affect the neighborhood,This may not lead to the best of all nodes said
5 Jumping Knowledge Networks
Big radius may lead to excessive average,And small radius may lead to instability or insufficient information together.因此,We put forward two simple but powerful architecture change——jump connection 和 subsequent selective But the polymerization mechanism of adaptive.
Figure 4 Illustrates the main ideas:In the common neighborhood aggregation network,Each layer through one is gathered before the size of the neighborhood to increase impact distribution.在最后一层,对于每个节点,We carefully from all these iterative said(它们“跳转”到最后一层)中选择,Potentially, combined with some.If this is for each node independently,Then the model can according to need to adjust the size of each node effective neighborhood,To get the required adaptive ability completely.
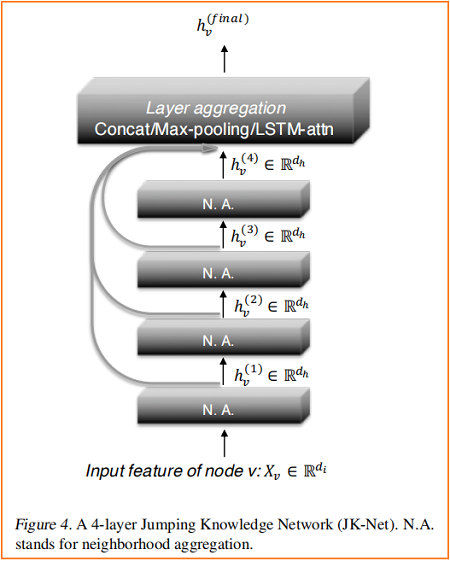
Our model allows the average layer aggregation mechanism.我们探索了三种方法;The other is possible.设 $h_{v}^{(1)}, \ldots, h_{v}^{(k)}$ Is to the aggregation node $v$ (来自 $k$ 个层)Jumps said.
Concatenation
直接拼接 $h_{v}^{(1)}, \ldots, h_{v}^{(k)}$Is the most direct way to combination of each layer,After can be linear transformation.If the conversion weights in figure between nodes to share,So this method is not a node adaptive.相反,It optimized weight,Combination in the form of the most suitable data sets subgraph features.People might think that connect the Yu Xiaotu and have regular structure、Adaptive less figure;Also because of weighted sharing helps reduce fitting.
$\max \left(h_{v}^{(1)}, \ldots, h_{v}^{(k)}\right)$ Choose the most information characteristics.例如,Said more local properties features coordinates can use learning from neighbor to coordinate,Those who said the state of the global features coordinates will benefit from higher.The biggest pooling is adaptive,Its advantage is not introduce any additional parameters to learn.
LSTM-attention
Pay attention to the mechanism by calculating each layer $l\left(\sum_{l} s_{v}^{(l)}=1\right)$ The attention of the score $s_{v}^{(l)}$ To identify each node $v$ The most useful neighborhood range,This represents a node $v$ 在第 $l$ Layer to learn the importance of the characteristics of the.节点 $v$ The characteristics of polymerization is said layer $\sum_{l} s_{v}^{(l)} \cdot h_{v}^{(l)}$ 的加权平均值.对于 LSTM 的注意力,我们输入 $h_{v}^{(1)}, \ldots, h_{v}^{(k)}$ 到 bi-directional LSTM ,And for each layer $l$ 生成 forward-LSTM 和 backward-LSTM 隐藏特征 $f_{v}^{(l)}$ 和 $b_{v}^{(l)}$.Connection characteristics of linear mapping $\left[f_{v}^{(l)} \| b_{v}^{(l)}\right]$ Produce a scalar importance scores $s_{v}^{(l)}$.对 $\left\{s_{v}^{(l)}\right\}_{l=1}^{k} $ 应用 Softmax Layer envoys point $v$ Within the scope of the different focus on the neighborhood.使节点 $v$ Within the scope of the different focus on the neighborhood.最后,我们取 $\left[f_{v}^{(l)} \| b_{v}^{(l)}\right]$ 的和,用 $SoftMax \left(\left\{s_{v}^{(l)}\right\}_{l=1}^{k}\right)$ 加权,Get the final layer of said.Another possible implementation is to LSTM 与 max-pooling 结合起来.LSTM-attention Is a node of adaptive,Because each node to the attention of the score is different.我们将看到,This method in large complex graph,Although because of the complexity of its relatively high,It may be in the picture(Less training node)上过拟合.
6 Experiments
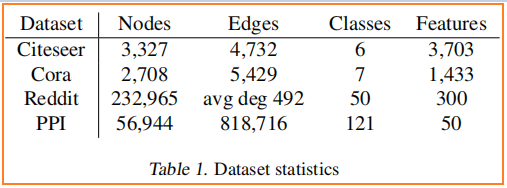
数据集
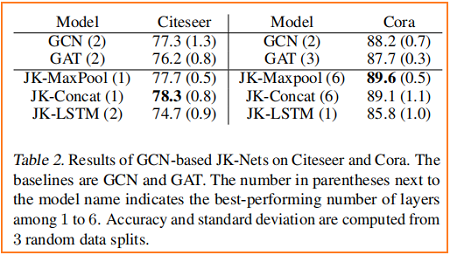
节点分类

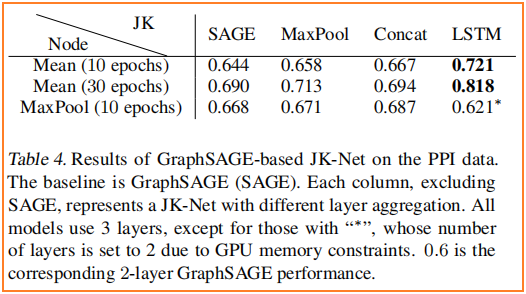
7 Conclusion


![[Unity Getting Started Plan] Basic Concepts (7) - Input Manager & Input Class](/img/a7/950ddc6c9eeaa56fe0c3165d22a7d2.png)