当前位置:网站首页>leetcode:333. 最大 BST 子树
leetcode:333. 最大 BST 子树
2022-06-10 20:55:00 【OceanStar的学习笔记】
题目来源
题目描述

题目解析
题目大概意思是:
- 给定一个二叉树,整体可能是,也可能不是二叉搜索树,但是它一定有子树是二叉搜索树,要找到节点数最多的子搜索二叉树的节点数
所以,本题需要解决两个问题:
- 找出二叉树中所有为BST的子树
- 返回最大的那个BST子树的节点数
这个最大的子搜索二叉树,有两种可能性:包含二叉树头节点,不包含二叉树头结点。
- 不包含头结点时:就需要知道左子树的最大搜索二叉树的节点数,右子树的最大搜索二叉树的节点数
- 包含头结点时:需要判断左树是不是搜索二叉树,右树是不是搜索二叉树,左树的最大值是否小于头节点,右树的最小值是否大于头节点,同时还需要左树和右树的节点数。
也就是说,root每次都需要问一问左子树和右子树:
- 最大满足二叉搜索树条件的子树有多少节点数
- 整个子树有多少节点数,整个子树的最大值、最小值是多少
- 是不是二叉搜索树
又因为,当最大搜索二叉树的节点数和节点数相等就意味着整个子树是搜索二叉树,所以可以化简为最大搜索二叉树的节点数、max、min、节点数。
所以,定义一个辅助类:
struct Info{
int maxBSTSubtreeSize;
int allSize;
int max;
int min;
explicit Info(int m, int a, int ma, int mi) {
maxBSTSubtreeSize = m;
allSize = a;
max = ma;
min = mi;
}
};
递归求解当前子树的info:
std::shared_ptr<Info> process(TreeNode *root){
if(root == nullptr){
return nullptr;
}
// 获取左右子树信息
auto leftInfo = process(root->left);
auto rightInfo = process(root->right);
// 拼凑自己的信息
int max = root->val, min = root->val, allSize = 1;
if(leftInfo != nullptr){
max = std::max(max, leftInfo->max);
min = std::min(min, leftInfo->min);
allSize += leftInfo->allSize;
}
if(rightInfo != nullptr){
max = std::max(max, rightInfo->max);
min = std::min(min, rightInfo->min);
allSize += rightInfo->allSize;
}
// [左|右]树 最大搜索二叉树大小
int p1 = -1, p2 = -1;
if(leftInfo != nullptr){
p1 = leftInfo->maxBSTSubtreeSize;
}
if(rightInfo != nullptr){
p2 = rightInfo->maxBSTSubtreeSize;
}
// 是否包含头节点
int p3 = -1;
bool leftSearch = leftInfo == nullptr || leftInfo->maxBSTSubtreeSize == leftInfo->allSize; // 左树是否是搜索二叉树
bool rightSearch = rightInfo == nullptr || rightInfo->maxBSTSubtreeSize == rightInfo->allSize; // 右树是否是搜索二叉树
if(leftSearch && rightSearch){
bool lessMaxLessX = leftInfo == nullptr || leftInfo->max < root->val; // 左树最大值是否比当前节点值小(空也认为比当前节点小)
bool rightMinMoreX = rightInfo == nullptr || rightInfo->min > root->val; // 右树最小值是否比当前节点值大(空也认为比当前节点大)
// 都满足,才能修改p3的值
if (lessMaxLessX && rightMinMoreX) {
int leftSize = leftInfo == nullptr ? 0 : leftInfo->allSize;
int rightSize = rightInfo == nullptr ? 0 : rightInfo->allSize;
p3 = leftSize + rightSize + 1;
}
}
// 最后修改,当前子树最大搜索二叉子树的大小
int maxSubSize = std::max(p1, std::max(p2, p3));
return std::make_shared<Info>(maxSubSize, max, min, allSize);
}
调用上面方法获取结果:
int maxSubSearchBinaryTreeSize(TreeNode *root){
if(root == nullptr){
return 0;
}
return process(root)->maxBSTSubtreeSize;
}
小结
二叉树递归套路总结:
- 1)假设以X节点为头,假设可以向X左树和X右树要任何信息
- 2)在上一步的假设下,讨论以X为头节点的树,得到答案的可能性(最重要)
- 3)列出所有可能性后,确定到底需要向左树和右树要什么样的信息
- 4)把左树信息和右树信息求全集,就是任何一棵子树都需要返回的信息S
- 5)递归函数都返回S,每一棵子树都这么要求
- 6)写代码,在代码中考虑如何把左树的信息和右树信息整合出整棵树的信息
边栏推荐
- 数组 求并集
- 2022-06-09 RK817 PMU 电池温度检测
- How to stimulate the vitality and driving force of cultural innovation
- 变量(自动变量、静态变量、寄存器变量、外部变量)与C的内存分配malloc/free、calloc/recalloc
- 【MySQL】表数据的增删查改(DML)
- Forward slash "/", backslash "\," escape character "\" and file path separator cannot be clearly remembered
- Apple zoom! It's done so well
- [NK] question de calcul de 51 g pour le match lunaire Bullock
- [nk] 牛客月赛51 G计算题
- Principle of gravure overprint and factors affecting overprint
猜你喜欢

Qingniao Changping campus of Peking University: can I learn UI with a high school degree?

Interpreting the new ecology of education in maker space
![[nk] 牛客月赛51 F-平均题](/img/b3/c36a0032e606f38fdc2f7c4562713c.png)
[nk] 牛客月赛51 F-平均题

Abbexa 8-OHdG CLIA kit solution

C#使用S7.net连接西门子S1200PLC,C#直接连接西门子PLC
SQL Server2019安装的详细步骤实战记录(亲测可用)

Abbexa AML1 DNA binding ELISA Kit instructions

JS mobile terminal copy text to clipboard code
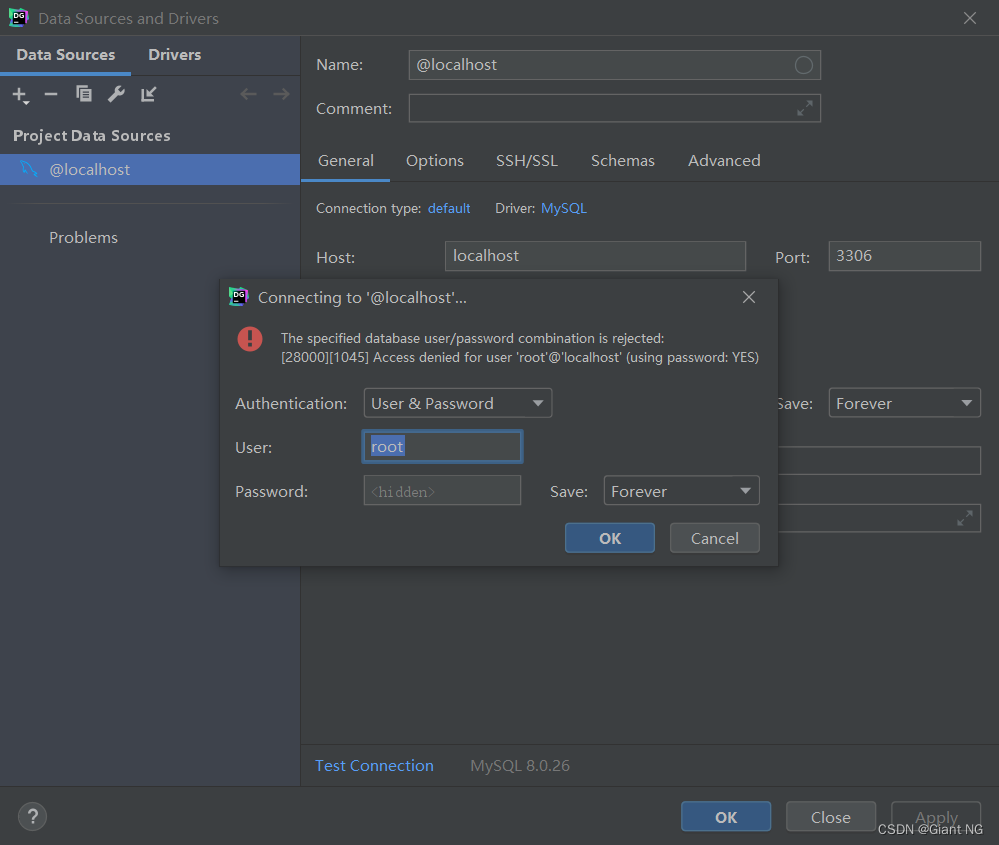
datagrip 报错 “The specified database user/password combination is rejected...”的解决方法
Detailed steps and actual records of SQL server2019 installation (available for hands-on test)
随机推荐
Back to table query of MySQL? How to avoid it?
Array move 0
Kdd2022 | neural network compression of depth map based on antagonistic knowledge distillation
SQL第四练:字符串处理函数
SQL Server row to column (pivot), column to row (unpivot)
在Oracle表中进行关键词搜索的过程
CentOS7环境下MySQL8常用命令小结
Ceph分布式存储集群Pool资源池的概念以及使用
【Microsoft Azure 的1024种玩法】七十五.云端数据库迁移之快速将阿里云RDS SQL Server无缝迁移到Azure SQL Databas
Self made table
[NK] question de calcul de 51 g pour le match lunaire Bullock
C中字符串查找
Qingniao Changping campus of Peking University: can I learn UI with a high school degree?
[nk] 牛客月賽51 G計算題
MySQL inserts query results into other tables
Use of C language qsort() function (detailed explanation)
Can I make up the exam if I fail the soft exam? Here comes the answer
[qingniaochangping campus of Peking University] the coordinated development of vocational education and general education, will this year's high school entrance examination be easy?
Array union set
2022-06-09 RK817 PMU 电池温度检测
