Distribution aware coordinate representation for human pose estimation

Reference resources ：

1. Look for generic representations ：CVPR 2020 There are three important solutions - cloud + Community - Tencent cloud

The goal of this article is Human attitude estimation （human pose estimation）, The main purpose is to detect any image The spatial position of human joints （ coordinate ）. Because of the light of each picture 、 The background and people's clothes are different , So the difficulty of this task is that the presentation of these joints in the picture changes a lot , Thus a good mark （ Coordinates of body joints ） Representation is particularly important . At present, the standard method for label characterization is to use Coordinate heat map (heatmap)—— A two-dimensional Gaussian distribution generated with the label coordinates of each joint as the core / nucleus [5], The core of this method is coordinate coding （ That is, the process from coordinates to heat map ） And decoding （ The process of returning from the heat map to the coordinates ）, And now SOTA The method is also based on heat maps . Therefore, the main purpose of this paper Is to improve the encoding and decoding method of heat map , At the same time, the importance of a good characterization is also proved by experiments .

The ultimate goal of the whole mission is Predict the joint coordinates of a given input image . So , You need to learn a regression model from the input image to the output coordinates . This process can be divided into two steps , First, suppose there is a set of training images , The learning of the model is divided into two steps ： The first step is the coding process ： Will node's ground truth The coordinates are encoded as a heat map as a supervised learning objective .

The second step is the decoding process ： During the test , The predicted heat map is decoded into coordinates in the original image coordinate space . In the process of coding , In order to reduce the amount of calculation , The resolution of the image pixels is attenuated , Therefore, it is necessary to offset the result in the decoding process to get a good result . In the past, the basic methods were Offset determined by experience , This paper explains the migration in detail , A better migration method is given . Again , When coding , It should also be transformed accordingly to avoid the impact of resolution attenuation .

Decoding of heat map 、 Quantization error and post-processing

decode ： The method based on heat map regression is in the reasoning stage , The process of obtaining the coordinates of the key points of the human body from the predicted heat map is called “ decode ”;

Quantization error ： Because of memory limitations , The size of heat map predicted by heat map regression is much smaller than that of the original map , So the real key coordinates have decimal parts , But the heat map is direct argmax When decoding , The resulting coordinates have only an integer part , Therefore has “ Quantization error ”;

post-processing ：DARK Previous “ Standard post-treatment ” Is in  Hourglass  Proposed in , That is, the prediction coordinate moves from the maximum value point to the second maximum value point 0.25 Pixels .

One 、 The decoding process

1.1 Standard decoding methods

Standard decoding methods It is determined by experience , Preliminary coordinates p It can be calculated from the following formula ：

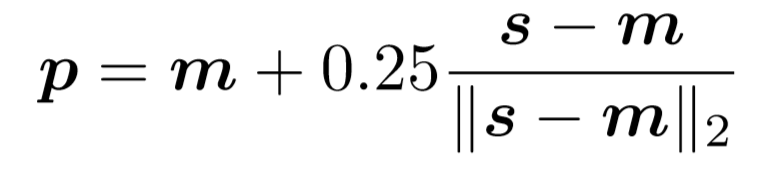
there m Is the maximum activation value in the heat map ,s Is the second largest active value in the heat map ,|| . ||_2 Is the module length of the vector .

P —— Predicted joint point position
m —— heatmap Coordinates at the maximum response in
s —— heatmap Coordinates of the second largest response in
That is to say, from peak to sub peak １／４ Position at offset , This method compensates the quantization error of down sampling when the original image is input into the network

in other words , The real coordinates should be shifted from the first largest activation value to the second largest activation value in the heat map space . The reason to offset , Because in the process of coding , In order to reduce the amount of calculation , The resolution of the image pixels is attenuated , Therefore, the position of the first largest activation value in the final heat map is not consistent with the actual position of the joint in the picture , It's just a rough assumption .

Suppose the initial decay rate is , The coordinates have been fixed by resolution （Resolution Recovery） The final coordinates after are ：

among λ yes resolution reduction ratio. Resolution reduction rate

1.2 Decoding implementation method

The decoding method proposed in this paper Take advantage of The distribution structure of the heat map , To find the true maximum activation value . The basic process is shown in the figure below .

（ The picture comes from the original paper ） chart 1： Decoding process structure diagram

Among them Resolution repair Consistent with standard methods （ As shown in the above formula ）.

Distribution-aware Maximum Relocalization It's based on Under the assumption of distribution Yes Maximum activation value for relocation . say concretely , The author of this article Assume Predicted heat map accord with 2D Gaussian distribution , And Actual heat map identical , therefore Predicted heat map Can be expressed as ：

there ( vector ) Is the position coordinate of a pixel on the heat map (),   Is the Gaussian kernel mean of the key point position to be predicted , That is, the value to be estimated .,   It's a constant , Never mind . Is the center of Gauss , This center is associated with the most important predicted joint position （ Position in the original picture ） relevant . covariance It's a diagonal matrix , Same as used in coordinate coding （ Is the standard deviation ）：

According to the principle of log likelihood optimization （Goodfellow,Bengio and Courville 2016）, On the premise of keeping the original position of the maximum activation value, the author uses logarithm to transform the original exponential form G Into a quadratic form P：

The ultimate goal of the whole task is to estimate , As an extreme point of distribution , as everyone knows , Location The first derivative of satisfies the following conditions ：

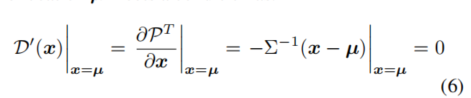
that       It is a harmony. A vector of the same shape ,  Because the real value is very close to the predicted value , The logarithmic heat map is at the maximum point    We're going to do a Taylor expansion at , Then the real key coordinates    The logarithmic heat map at can be written as

among    Is the maximum point on the logarithmic heat map m  The first order of 、 Second derivative .

Yes （7） type On both sides at the same time    Derivation , obtain ：

because    Is the center of the Gaussian distribution , , Into the (4) After formula simplification, we get ：

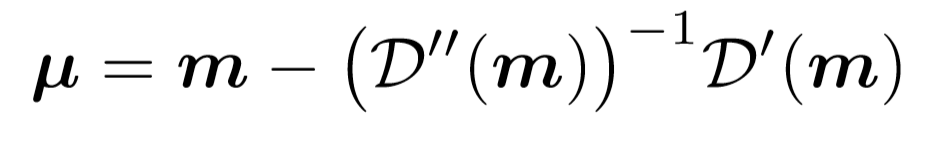
( See for formula derivation ：Dark Estimate the mean position of the true distribution of key points ) 

1.3 Distribution Modulation（ Distributed modulation ）

The proposed coordinate decoding method is based on the assumption that the predicted heat map is Gaussian distribution , But usually , The heat map predicted by the human posture estimation model is compared with the heat map data after training , Does not show a good Gaussian structure .

As shown in the figure , The predicted heat map usually has multiple peaks near the maximum activation point . This may have a negative impact on the performance of our decoding method . To solve this problem , We suggest that the predicted heat map distribution be adjusted in advance ,

From predicted heatmap --> Modulated Heatmap

The concrete way is ： Check with Gauss predicted heatmap Make it smooth

Therefore, the author uses a Gaussian kernel with the same discreteness as the training data K To predict the heat map h Modulation （ Convolution ）, To mitigate the effects of multiple peaks ：

In order to keep the original heatmap Size , We are finally right h’ Scaled , Make its maximum activation equal to h The maximum activation quantity of proves the consistency of values before and after modulation , The author also makes a scale change ：

Summary of decoding process ：

1. Heat map distribution modulation
2. Joint localization by Taylor expansion with sub-pixel accuracy .
3. Restore the resolution to the original space

1.4 Coordinate coding process

In this part, the author tries to solve the same problem as decoding , take gound-truth（ Joint coordinates ） First, the conversion is carried out to reduce the effect of resolution attenuation , Then regenerate the heat map . say concretely , The author first gives a brief introduction to ground-truth（g=(u,v)） Perform pixel attenuation （ For the decay rate ） obtain g'：

Then in order to facilitate the generation of nuclei , The author also quantifies it （quantise(), Can be rounded down , Rounding up , Rounding, etc ） So that we can finally get g"：

Finally, with this coordinate (g'') A heat map centered on ：

And then , To quantify coordinates g’‘ Centered heat maps can be synthesized in the following ways :

Due to the existence of quantization error , The heat map generated in the above way is generated by the deviation , Inaccurate , As shown in the figure .

This figure mainly illustrates the quantization error . Blue dot representation g’ The exact location of the , Based on floor The quantitative operation of , There is an error （ The red arrow ）, Other quantitative methods have the same problem .
resolvent ： Before using non quantitative g’ Represents the quantification center , Put the equation 14 Medium g’’ use g’ Instead of , We will demonstrate the benefits of this unbiased heat map generation method ( surface 3). as follows ：

The benefits of this unbiased heat map , As shown in the table 3：

Thesis code open source ：

GitHub - ilovepose/DarkPose: Distribution-Aware Coordinate Representation for Human Pose Estimation

Inside readme It's very detailed ;

function ：

output：