你了解数据是如何存储的吗？（C整型和浮点型两类）

通常普通程序员是不会去了解这些比较底层的东西的，因为就暂且来看确实了解这些东西帮助不会很大，但是对于热爱编程的我来说，热爱它就应该从里到外的了解它，况且我们每天学一点别人不愿意学的新知识就和别人拉开一点距离，日积月累大佬就形成了，加油少年，这是一个拼搏的时代！

本篇博客介绍重点如下：

  1.数据类型介绍

  2.整型的原，反，补码

  3.大小端字节序介绍和判断

  4.浮点型在内存中的存储解

目录

一.数据类型介绍

 1.基本内置类型

 2.类型基本归类

  

二.整型在内存中的存储

1.了解原，反，补码

  2.介绍unsigned无符号和signed有符号区别

3.大小端

三.浮点数在内存中的存储

一.数据类型介绍

 1.基本内置类型

char                           //字符数据类型

short                          //短整型

int                              //整型

long                           //长整型

long long                  //更长整型

float                          //单精度浮点型

double                     //双精度浮点型        

类型的意义：

1.类型决定使用空间的大小，大小决定使用范围

2.类型决定看待内存空间的角度不同（整型和浮点型存储方式不一样）

 2.类型基本归类

                                                      整型家族

char： 

  unsigned char          

  signed char              

short：

unsigned short

signed  short

int：

unsigned int

signed  int

        

 long：

unsigend long

signed long

除了char以外其他类型都分为unsigend（无符号） 和 sigend（有符号）类型，我们平常所写的 int n = 10；这里的int默认等价于sigend int类型，但是对于char属于什么类型标准是未定义的，取决于编译器的实现；

                                                       浮点家族

float                   //单精度浮点型

double              //双精度浮点型

                                                     构造类型

数组类型

结构体类型    struct

枚举类型       enum

联合类型       union

                                                     指针类型

int   *pi

char   *pc

float   *pd

void    *pv

  

二.整型在内存中的存储

1.了解原，反，补码

计算机的整数总共有三种二进制表达方式，即原，反，补码；

三种方式均有符号位和数值位，符号位0表示正，1表示负；正数的数值位原反补码都相同；

负数的数值位：

原码：   直接将数值按照正负数的形式翻译成二进制就可以得到原码。

反码：  将原码的符号位不变，其他位依次按位取反就可以得到反码。

补码：  反码+1就得到补码。

 *  对于整数而言，数据在内存中存放的就是补码，给我们看到的都是原码；

问：为什么要大费周折的创建3种二进制表达形式，直接存原码不行吗？

*在计算机系统中，数值一律用补码来表示和存储。原因在于，使用补码，可以将符号位和数值域统 一处理； 同时，加法和减法也可以统一处理（CPU只有加法器）此外，补码与原码相互转换，其运算过程 是相同的，不需要额外的硬件电路。

 也就是说CPU只能计算加法，那么减法怎么计算呢？我们可以将它转换一下：

1-1 ------>  1+（-1）

但是到这里你就可以发现如果我们用原码的形式存放数据进行1+（-1）：

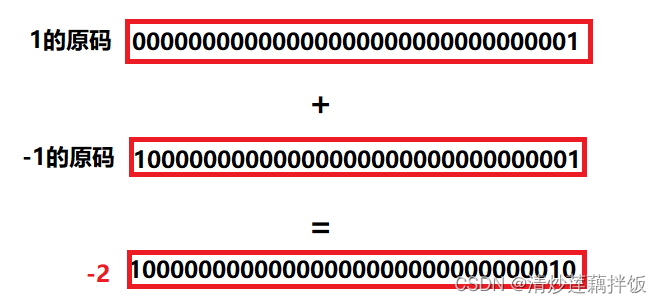
 结果等于-2了，这完全不合理；所以科学家们就发明了以补码的形式进行存储，正好可以计算：

是不是很神奇，这也就是补码的意义！

  2.介绍unsigned无符号和signed有符号区别

介绍前我们先来看一段代码，这段代码输出什么？

#include <stdio.h>
int main()
{
    char a= -1;
    signed char b=-1;
    unsigned char c=-1;
    printf("a=%d,b=%d,c=%d",a,b,c);
    return 0;
}

题目思路：

我们已经了解了有符号和无符号类型，那么我们就按照它们的特性分别来推理它们的结果，有符号顾名思义它的二进制最高位就是符号位，符号位不参与数值的计算；无符号就是在二进制中它的最高位不是符号位，是会直接参与到数值的计算的；那么大家对上面的代码是不是会有一个新的认识呢？（下图是举一个栗子）

️题解 ：

a的值：前面我们说过char比较特殊，它是有符号的还是无符号的取决于编译器；

b的值：b在题目中明确表明了它是有符号的，所以它是一个负数，通过原反补码定律得到它的原码是-1，所以b的值是-1；

c的值：c是一个无符号类型，所以这里我们着重探讨一下c的值；

  1.首先将-1的赋值给unsigned char c，发生整型提升；

2.因为内存中存放的是补码，所以我们进行换算

3.因为c是char类型，空间不够发生了截断

4.因为c是无符号整型，所以11111111就是它的值，有请计算机：

所以c的值应该是255 ；

 

讲到这里大家应该了解了有符号和无符号的区别了吧，虽然只是小知识点，但是大家以后遇到类似的问题能够第一时间解决我就认为这些都是值得的，大家的努力都不会白费的

3.大小端

#include<stdio.h>
int main()
{
	int a = 20;
	int b = -10;
	return 0;
}

a的十六进制表达（补码）：0x 00  00  00  14   （一对00大小代表一个字节）

b的十六进制表达（补码）：0x  f f    f f     f f    f 6 

用这段代码我们来查看内存中的存储：

 这里存储的方式是小端存储；

大小端介绍：

大端（存储）模式，是指数据的低位保存在内存的高地址中，而数据的高位，保存在内存的低地址 中；

小端（存储）模式，是指数据的低位保存在内存的低地址中，而数据的高位,，保存在内存的高地 址中。

为什么会有大小端存储方式：

为什么会有大小端模式之分呢？这是因为在计算机系统中，我们是以字节为单位的，每个地址单元 都对应着一个字节，一个字节为8 bit。但是在C语言中除了8 bit的char之外，还有16 bit的short 型，32 bit的long型（要看具体的编译器），另外，对于位数大于8位的处理器，例如16位或者32 位的处理器，由于寄存器宽度大于一个字节，那么必然存在着一个如何将多个字节安排的问题。因 此就导致了大端存储模式和小端存储模式。 例如：一个 16bit 的 short 型 x ，在内存中的地址为 0x0010 ， x 的值为 0x1122 ，那么 0x11 为 高字节， 0x22 为低字节。对于大端模式，就将 0x11 放在低地址中，即 0x0010 中， 0x22 放在高 地址中，即 0x0011 中。小端模式，刚好相反。我们常用的 X86 结构是小端模式，而 KEIL C51 则 为大端模式。很多的ARM，DSP都为小端模式。有些ARM处理器还可以由硬件来选择是大端模式 还是小端模式。

️ 题：写一个程序判断当前系统大小端；

思路：判断大小端也就是想要我们判断一个数在内存中是怎样存放的，例如int n = 1它的首地址存放的应该是0或者1，我们需要单单只需要将它的第一个字节内容取出来然后判断就可以了；代码如下：

#include <stdio.h>
int check_sys()
{
 int i = 1;
 return (*(char *)&i);
}
int main()
{
 int ret = check_sys();
 if(ret == 1)
 {
 printf("小端\n");
 }
 else
 {
 printf("大端\n");
 }
 return 0;
}

三.浮点数在内存中的存储

浮点数存储代码例子：

int main()
{
 int n = 9;
 float *pFloat = (float *)&n;
 printf("n的值为：%d\n",n);
 printf("*pFloat的值为：%f\n",*pFloat);
 *pFloat = 9.0;
 printf("num的值为：%d\n",n);
 printf("*pFloat的值为：%f\n",*pFloat);
 return 0;
}

输出结果：

 看完这个代码和输出结果大家是不是又懵逼了呢？不急，下面让我一一来给大家讲解浮点数的存储规则；

国际标准IEEE 754规定，任何一个二进制浮点数V都可以用下面的形式表达：

公式------  (-1)^S * M * 2^E

(-1)^S表示符号位，当S=0，V为正数；当S=1，V为负数。

M表示有效数字，大于等于1，小于2。

2^E表示指数位。

举个栗子：

栗子1：十进制的5.0用二进制表示是101.0，在二进制中也就是1.01 * 2^2（次方），按照上面的IEEE标准我们可以知道S = 0，M = 1.01，指数 E = 2；

栗子2：十进制的-5.0用二进制表示是-101.0，在二进制中也就是-1.01 * 2^2（次方），按照上面的IEEE标准我们可以知道S = 1，M = 1.01，指数 E = 2；

对于浮点数分别为单精度和双精度存放的规则：

IEEE 754对有效数字M和指数E，还有一些特别规定。

 前面说过， 1≤M<2 ，也就是说，M可以写成 1.xxxxxx 的形式，其中xxxxxx表示小数部分。 IEEE 754规定，在计算机内部保存M时，默认这个数的第一位总是1，因此可以被舍去，只保存后面的 xxxxxx部分。比如保存1.01的时 候，只保存01，等到读取的时候，再把第一位的1加上去。这样做的目的，是节省1位有效数字。以32位 浮点数为例，留给M只有23位， 将第一位的1舍去以后，等于可以保存24位有效数字。

至于指数E，情况就比较复杂。

 首先，E为一个无符号整数（unsigned int） 这意味着，如果E为8位，它的取值范围为0~255；如果E为11位，它的取值范围为0~2047。但是，我们 知道，科学计数法中的E是可以出 现负数的，所以IEEE 754规定，存入内存时E的真实值必须再加上一个中间数，对于8位的E，这个中间数 是127；对于11位的E，这个中间 数是1023。比如，2^10的E是10，所以保存成32位浮点数时，必须保存成10+127=137，即 10001001。

 然后，指数E从内存中取出还可以再分成三种情况：

1.E不全为0或不全为1

这时，浮点数就采用下面的规则表示，即指数E的计算值减去127（或1023），得到真实值，再将 有效数字M前加上第一位的1。

比如： 0.5（1/2）的二进制形式为0.1，由于规定正数部分必须为1，即将小数点右移1位，则为 1.0*2^(-1)，其阶码为-1+127=126，表示为 01111110，而尾数1.0去掉整数部分为0，补齐0到23位00000000000000000000000，则其二进 制表示形式为:

0 01111110 00000000000000000000000

2.E全为0

这时，浮点数的指数E等于1-127（或者1-1023）即为真实值， 有效数字M不再加上第一位的1，而是还原为0.xxxxxx的小数。这样做是为了表示±0，以及接近于 0的很小的数字。

3.   E全为1     

这时，如果有效数字M全为0，表示±无穷大（正负取决于符号位s）；

️那我们再回到题目：

int main()
{
 int n = 9;
 float *pFloat = (float *)&n;
 printf("n的值为：%d\n",n);
 printf("*pFloat的值为：%f\n",*pFloat);
 *pFloat = 9.0;
 printf("num的值为：%d\n",n);
 printf("*pFloat的值为：%f\n",*pFloat);
 return 0;
}

思路：

第一个打印：

直接以整型打印n所以n的值就是9；

第二个打印：

将n的值以浮点数访问并打印，那么他就会认为9的二进制表达式是一个浮点数，所以根据公式(-1)^S * M * 2^E得到：

+ 0.00000000000000000001001 * 2 ^ -126

这是一个无限接近0的浮点数，可是我们空间有限所以打印0.000000

第三个打印：

将n的内容进行浮点数的方式存储9.0，然后以整型的形式打印：

1.001 * 2 ^ 3        S = 0,   E = 3,   M = 1.001  得到二进制：

      01000001000100000000000000000000

以整型打印：

第四次打印：

n的内容是浮点数的方式存储的9.0，然后以浮点数的形式打印： 以浮点数方式存以浮点数方式取 ，结果肯定是9.0了；

️在学习的过程中也要注意自己的身体，健康的身体才能支撑我们的理想；如果你喜欢本篇博客，三连支持一下博主吧