当前位置:网站首页>洛谷P4127 [AHOI2009]同类分布 题解
洛谷P4127 [AHOI2009]同类分布 题解
2022-07-06 07:23:00 【q779】
洛谷P4127 [AHOI2009]同类分布 题解
题目链接:P4127 [AHOI2009]同类分布
题意:
给出两个数 a , b a,b a,b ,求出 [ a , b ] [a,b] [a,b] 中各位数字之和能整除原数的数的个数。
对于所有的数据, 1 ≤ a ≤ b ≤ 1 0 18 1 ≤ a ≤ b ≤ 10^{18} 1≤a≤b≤1018。
明天就期末考了非但不复习还在刷题 qwqqwqwq
因为我们不能确切知道每个数的数位和
但是我们知道它们一定在 [ 1 , 9 × l ] [1,9 \times l] [1,9×l] 的范围内( l l l 为最长的位数)
我们枚举所有的数位和并计算每个数位和对应的答案
把这些答案加起来就是 [ 0 , x ] [0,x] [0,x] 的答案
[ a , b ] [a,b] [a,b] 的答案可以拆分为两个询问 [ 0 , b ] [0,b] [0,b] 和 [ 0 , a − 1 ] [0,a-1] [0,a−1]
而这里 a , b ≤ 1 0 18 a,b \le 10^{18} a,b≤1018 ,直接压入状态显然不可接受
于是我们可以考虑记录模当前枚举的数位和意义下的数
方便起见,我们称当前枚举的数位和为 m m m
设 f i , j , k f_{i,j,k} fi,j,k 表示只考虑前 i i i 位数(包括前导零),前 i i i 位的数位和为 j j j ,当前数模 m m m 为 k k k 时的答案
不难发现
f i , j , k = ∑ 0 ≤ d ≤ t f i + 1 , j + d , ( k × 10 + d m o d m ) f_{i,j,k} = \sum_{0 \le d \le t} f_{i+1,j+d,\left(k\times 10 + d \, \bmod \, m\right)} fi,j,k=0≤d≤t∑fi+1,j+d,(k×10+dmodm)
其中 t t t 为第 i + 1 i+1 i+1 位的高位限制
用记搜写法能简洁不少
时间复杂度 O ( 9 3 × l 4 ) O(9^3\times l^4) O(93×l4)
代码:
#include <iostream>
#include <string>
#include <vector>
#include <algorithm>
#include <cstdio>
#include <cstdlib>
#include <cstring>
#include <cmath>
#include <iomanip>
using namespace std;
#define int long long
#define INF 0x3f3f3f3f3f3f3f3f
#define N (int)()
int len,num[25],f[25][205][205];
int dfs(int u,int sum,int st,int limit,int p)
{
if(u>len)
{
if(!sum)return 0;
return st==0&&sum==p;
}
if(!limit&&f[u][sum][st]!=INF)
return f[u][sum][st];
int up=limit?num[len-u+1]:9;
int res=0;
for(int i=0; i<=up; i++)
res+=dfs(u+1,sum+i,(10*st+i)%p,limit&&i==up,p);
return limit?res:f[u][sum][st]=res;
}
int solve(int x)
{
int res=0; len=0;
while(x) num[++len]=x%10,x/=10;
for(int m=1; m<=9*len; m++)
{
memset(f,0x3f,sizeof(f));
res+=dfs(1,0,0,1,m);
}
return res;
}
signed main()
{
ios::sync_with_stdio(0);
cin.tie(0);cout.tie(0);
// freopen("check.in","r",stdin);
// freopen("check.out","w",stdout);
int l,r; cin >> l >> r;
cout << solve(r)-solve(l-1) << '\n';
return 0;
}
没事反正whk暂时开摆了
转载请说明出处
边栏推荐
- How to delete all the words before or after a symbol in word
- If Jerry's Bluetooth device wants to send data to the mobile phone, the mobile phone needs to open the notify channel first [article]
- Related operations of Excel
- How can word delete English only and keep Chinese or delete Chinese and keep English
- Chrome view page FPS
- Multi attribute object detection on rare aircraft data sets: experimental process using yolov5
- Wechat brain competition answer applet_ Support the flow main belt with the latest question bank file
- Path analysis model
- Ble of Jerry [chapter]
- Detailed explanation | detailed explanation of internal mechanism of industrial robot
猜你喜欢
Upgraded wechat tool applet source code for mobile phone detection - supports a variety of main traffic modes
![Ble of Jerry [chapter]](/img/d8/d080ccaa4ee530ed21d62755808724.png)
Ble of Jerry [chapter]
SSM learning

The ECU of 21 Audi q5l 45tfsi brushes is upgraded to master special adjustment, and the horsepower is safely and stably increased to 305 horsepower

【mysql学习笔记30】锁(非教程)
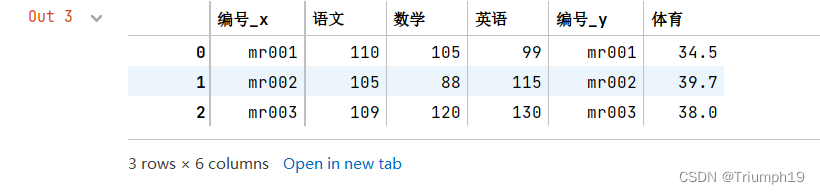
Set picture annotation in markdown
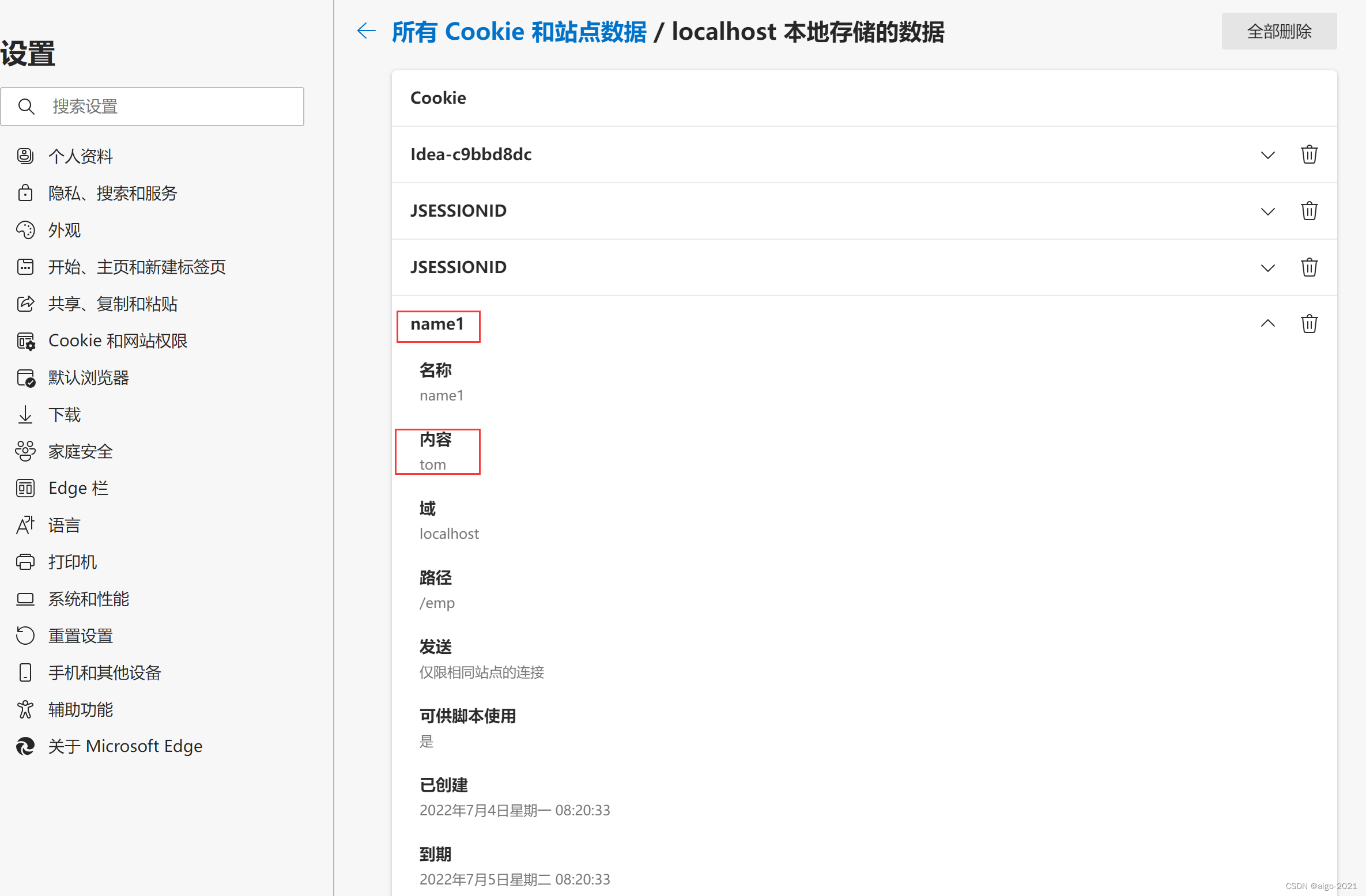
Cookie技术&Session技术&ServletContext对象

杰理之蓝牙设备想要发送数据给手机,需要手机先打开 notify 通道【篇】
Summary of Digital IC design written examination questions (I)

Multi attribute object detection on rare aircraft data sets: experimental process using yolov5
随机推荐
Uni app third party package configuration network request
leetcode1020. Number of enclaves (medium)
Jerry's ad series MIDI function description [chapter]
Configure raspberry pie access network
Set picture annotation in markdown
Yield method of tread
杰理之如若需要大包发送,需要手机端修改 MTU【篇】
SSM learning
杰理之蓝牙设备想要发送数据给手机,需要手机先打开 notify 通道【篇】
可变参数重载时的内存错误
TypeScript 可索引类型
智能终端设备加密防护的意义和措施
CDN acceleration and cracking anti-theft chain function
C - Inheritance - hidden method
On the world of NDK (2)
word删除括号里内容
GET/POST/PUT/PATCH/DELETE含义
Week6 weekly report
Ble of Jerry [chapter]
杰理之AD 系列 MIDI 功能说明【篇】