动手学深度学习_softmax回归

目录

分类问题

softmax运算

交叉熵损失

pytorch实现​​​​​​​

分类问题

        前面一节讲了线性回归，线性回归更多地使用在预测多少的问题。在实际问题中，我们还对“哪一个”感兴趣，也就是分类问题。

        分类问题与回归问题最大的不同就是，回归最后的输出是一个值，但是分类问题输出的是一系列关于类别的置信度。

        我们从一个图像分类问题开始。 假设每次输入是一个2×2的灰度图像。 我们可以用一个标量表示每个像素值，每个图像对应四个特征x1,x2,x3,x4。 此外，假设每个图像属于类别“猫”，“鸡”和“狗”中的一个。

        接下来，我们要选择如何表示标签。 我们有两个明显的选择：最直接的想法是选择y∈{1,2,3}， 其中整数分别代表{狗,猫,鸡}。 这是在计算机上存储此类信息的有效方法。 如果类别间有一些自然顺序， 比如说我们试图预{婴儿,儿童,青少年,青年人,中年人,老年人}， 那么将这个问题转变为回归问题，并且保留这种格式是有意义的。

        但是一般的分类问题并不与类别之间的自然顺序有关。 幸运的是，统计学家很早以前就发明了一种表示分类数据的简单方法：独热编码（one-hot encoding）。 独热编码是一个向量，它的分量和类别一样多。 类别对应的分量设置为1，其他所有分量设置为0。 在我们的例子中，标签y将是一个三维向量， 其中(1,0,0)对应于“猫”、(0,1,0)对应于“鸡”、(0,0,1)对应于“狗”：

        为了估计所有可能类别的条件概率，我们需要一个有多个输出的模型，每个类别对应一个输出。         为了解决线性模型的分类问题，我们需要和输出一样多的仿射函数（affine function）。 每个输出对应于它自己的仿射函数。 在我们的例子中，由于我们有4个特征和3个可能的输出类别， 我们将需要12个标量来表示权重（带下标的w）， 3个标量来表示偏置（带下标的b）。 下面我们为每个输入计算三个未规范化的预测（logit）：o1、o2和o3。

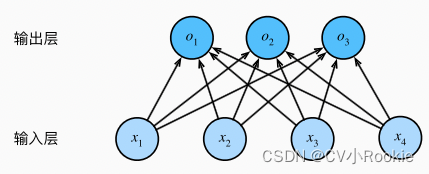
         与线性回归一样，softmax回归也是一个单层神经网络。 由于计算每个输出o1、o2和o3取决于 所有输入x1、x2、x3和x4， 所以softmax回归的输出层也是全连接层。

向量形式表达：，这里的W区别于线性回归的 w，在这里是一个矩阵。

softmax运算

        首先给出softmax的公式： 

        其实根据公式就可以看出，softmax先是利用指数函数先把输出变为非负，再通过除以总和确保最后的输出总和为1。

        尽管softmax是一个非线性函数，但softmax回归的输出仍然由输入特征的仿射变换决定。 因此，softmax回归是一个线性模型（linear model）。

交叉熵损失

交叉熵常用来衡量两个概率的区别：  .

对于所有的样本来说我们有  ，那么损失函数就是：  。对于这个公式，我们把它称为交叉熵损失（cross-entropy loss）。

pytorch实现

# 作者 ：CV小Rookie
# 创建时间： 2022/7/29 20:13
# 文件名： softmax_easy.py
import torch
from torch import nn
from d2l import torch as d2l


batch_size = 256
train_iter, test_iter = d2l.load_data_fashion_mnist(batch_size)

net = nn.Sequential(nn.Flatten(), nn.Linear(784, 10))

def init_weights(m):
    if type(m) == nn.Linear:
        nn.init.normal_(m.weight, std=0.01)

net.apply(init_weights);

loss = nn.CrossEntropyLoss(reduction='none')

trainer = torch.optim.SGD(net.parameters(), lr=0.1)

num_epochs = 10

d2l.train_ch3(net, train_iter, test_iter, loss, num_epochs, trainer)
d2l.plt.show()