Detailed explanation and application of merging and sorting

Algorithm ideas

Let's just say that , All recursive algorithms , You don't care what it does , It's essentially traversing a tree （ recursive ） Trees , And then at the node （ Front, middle and rear positions ） Execute code on , You have to write recursive algorithms , In essence, it is to tell each node what to do .

Look at the code framework of merging and sorting :

//  Definition ： Sort  nums[lo..hi]
void sort(int[] nums, int lo, int hi) {
    
    if (lo == hi) {
    
        return;
    }
    int mid = (lo + hi) / 2;
    //  Using definitions , Sort  nums[lo..mid]
    sort(nums, lo, mid);
    //  Using definitions , Sort  nums[mid+1..hi]
    sort(nums, mid + 1, hi);

    /******  Post sequence position  ******/
    //  At this point, the two molecular arrays have been ordered 
    //  Merge two ordered arrays , send  nums[lo..hi]  Orderly 
    merge(nums, lo, mid, hi);
    /*********************/
}

//  Put an ordered array  nums[lo..mid]  And ordered arrays  nums[mid+1..hi]
//  Merge into an ordered array  nums[lo..hi]
void merge(int[] nums, int lo, int mid, int hi);

Look at this frame , I understand the classic summary ： Merge sort is to sort the left-hand array first , Then put the right half of the array in order , Then merge the two halves of the array .

The above code is very similar to the post order traversal of binary tree ：

/*  Binary tree traversal framework  */
void traverse(TreeNode root) {
    
    if (root == null) {
    
        return;
    }
    traverse(root.left);
    traverse(root.right);
    /******  Post sequence position  ******/
    print(root.val);
    /*********************/
}

above Binary tree （ Programme ） The binary tree problem can be divided into two kinds of ideas , One is the idea of traversing a binary tree , The other is the idea of decomposing the problem , According to the above analogy , Obviously, merging and sorting uses the idea of decomposing the problem

The process of merging and sorting can be logically abstracted into a binary tree , The value of each node in the tree can be considered as nums[lo..hi], The value of the leaf node is a single element in the array ：

then , In the sequential position of each node （ The left and right child nodes have been arranged in order ） When it comes to execution merge function , Merge subarrays on two child nodes ：

Code implementation and Analysis

《 Algorithm 4》 The merge sort code given in has the characteristics of simplicity and efficiency , So we can refer to the code given in the book as the merging algorithm template ：

class Merge {
    

    //  Used to help merge ordered arrays 
    private static int[] temp;

    public static void sort(int[] nums) {
    
        //  First open up memory space for the auxiliary array 
        temp = new int[nums.length];
        //  Sort entire array （ Modify in place ）
        sort(nums, 0, nums.length - 1);
    }

    //  Definition ： Sub array  nums[lo..hi]  Sort 
    private static void sort(int[] nums, int lo, int hi) {
    
        if (lo == hi) {
    
            //  Individual elements do not need to be sorted 
            return;
        }
        //  This is written to prevent overflow , The effect is equivalent to  (hi + lo) / 2
        int mid = lo + (hi - lo) / 2;
        //  First on the left half of the array  nums[lo..mid]  Sort 
        sort(nums, lo, mid);
        //  Then on the right half of the array  nums[mid+1..hi]  Sort 
        sort(nums, mid + 1, hi);
        //  Combine two parts of an ordered array into one 
        merge(nums, lo, mid, hi);
    }

    //  take  nums[lo..mid]  and  nums[mid+1..hi]  The two ordered arrays are combined into an ordered array 
    private static void merge(int[] nums, int lo, int mid, int hi) {
    
        //  The first  nums[lo..hi]  Copy to auxiliary array 
        //  So that the combined results can be directly stored in  nums
        for (int i = lo; i <= hi; i++) {
    
            temp[i] = nums[i];
        }

        //  Array double pointer technique , Merge two ordered arrays 
        int i = lo, j = mid + 1;
        for (int p = lo; p <= hi; p++) {
    
            if (i == mid + 1) {
    
                //  The left half of the array has been merged 
                nums[p] = temp[j++];
            } else if (j == hi + 1) {
    
                //  The right half of the array has been merged 
                nums[p] = temp[i++];
            } else if (temp[i] > temp[j]) {
    
                nums[p] = temp[j++];
            } else {
    
                nums[p] = temp[i++];
            }
        }
    }
}

With the foreshadowing , Here we just need to focus on this merge function .

sort Function pair nums[lo..mid] and nums[mid+1..hi] After recursive sorting , We can't merge them in place , So we need to copy To temp In an array , And then through something similar to the above Six skills of single linked list The double pointer technique of merging ordered linked lists in nums[lo..hi] Merge into an ordered array ：

Notice that we're not merge Function execution time new Auxiliary array , It's about putting... In advance temp Auxiliary array new Come out , So you It avoids the possible performance problems caused by frequent allocation and release of memory in recursion .

Again, the time complexity of merging and sorting , Although everyone should know that O(NlogN), But not everyone knows how to calculate this complexity .

above Dynamic planning details Said the complexity calculation of recursive algorithm , Namely Number of sub questions x The complexity of solving a subproblem . For merge sort , The time complexity is obviously concentrated in merge Ergodic function nums[lo..hi] The process of , But every time merge Input lo and hi All different , Therefore, it is not easy to see the time complexity intuitively .

The number of execution times is the number of binary tree nodes , The complexity of each execution is the length of the subarray represented by each node , So the total time complexity is in the whole tree 「 Array elements 」 The number of .

So on the whole , The height of this binary tree is logN, The number of elements in each layer is the length of the original array N, So the total time complexity is O(NlogN).

Other applications

In addition to the most basic sorting problem , Merging and sorting can also be used to solve the problem of force deduction 315 topic 「 Count the number of elements on the right less than the current one 」：

Let's not talk about the violent solution of patting our heads , nesting for loop , Square level complexity .

What does this question have to do with merging and sorting , Mainly in the merge function , We are using merge Function when merging two ordered arrays , In fact, you can know an element nums[i] How many elements are there behind nums[i] Small .

say concretely , For example, this scene ：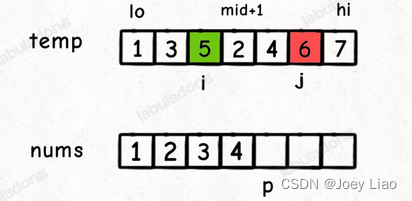

At this time, we should put temp[i] Put it in nums[p] On , because temp[i] < temp[j].

But in this scenario , We can also know a message ：5 Rear ratio 5 The small number of elements is Left closed right open interval [mid + 1, j) The number of elements in , namely 2 and 4 These two elements ：

let me put it another way , In the face of nuns[lo..hi] In the process of merging , Whenever executed nums[p] = temp[i] when , You can be sure temp[i] The number of elements smaller than this element is j - mid - 1.

Of course ,nums[lo..hi] Itself is just a sub array , This subarray will be executed later merge, Of the elements The position will still change . But this is a problem that other recursive nodes need to consider , All we have to do is merge Do some tricks in the function , Stack each time merge The results recorded at .

class Solution {
    private class Pair {
        int val, id;
        Pair(int val, int id) {
            //  Record the element value of the array 
            this.val = val;
            //  Record the original index of the element in the array 
            this.id = id;
        }
    }
    
    //  Auxiliary array used for merging and sorting 
    private Pair[] temp;
    //  Record the number of elements smaller than yourself after each element 
    private int[] count;
    
    //  The main function 
    public List<Integer> countSmaller(int[] nums) {
        int n = nums.length;
        count = new int[n];
        temp = new Pair[n];
        Pair[] arr = new Pair[n];
        //  Record the original index position of the element , In order to be in  count  Update the result in the array 
        for (int i = 0; i < n; i++)
            arr[i] = new Pair(nums[i], i);
        
        //  Perform merge sort , The result of this question is recorded in  count  Array 
        sort(arr, 0, n - 1);
        
        List<Integer> res = new LinkedList<>();
        for (int c : count) res.add(c);
        return res;
    }
    
    //  Merge sort 
    private void sort(Pair[] arr, int lo, int hi) {
        if (lo == hi) return;
        int mid = lo + (hi - lo) / 2;
        sort(arr, lo, mid);
        sort(arr, mid + 1, hi);
        merge(arr, lo, mid, hi);
    }
    
    //  Merge two ordered arrays 
    private void merge(Pair[] arr, int lo, int mid, int hi) {
        for (int i = lo; i <= hi; i++) {
            temp[i] = arr[i];
        }
        
        int i = lo, j = mid + 1;
        for (int p = lo; p <= hi; p++) {
            if (i == mid + 1) {
                arr[p] = temp[j++];
            } else if (j == hi + 1) {
                arr[p] = temp[i++];
                //  to update  count  Array 
                count[arr[p].id] += j - mid - 1;
            } else if (temp[i].val > temp[j].val) {
                arr[p] = temp[j++];
            } else {
                arr[p] = temp[i++];
                //  to update  count  Array 
                count[arr[p].id] += j - mid - 1;
            }
        }
    }
}

Because in the sorting process , The index position of each element will change constantly , So we use a Pair Class encapsulates each element and its in the original array nums Index in , In order to count Array records the number of elements less than it after each element .

Flip it right

Take a look at the force buckle 493 topic 「 Flip it right 」

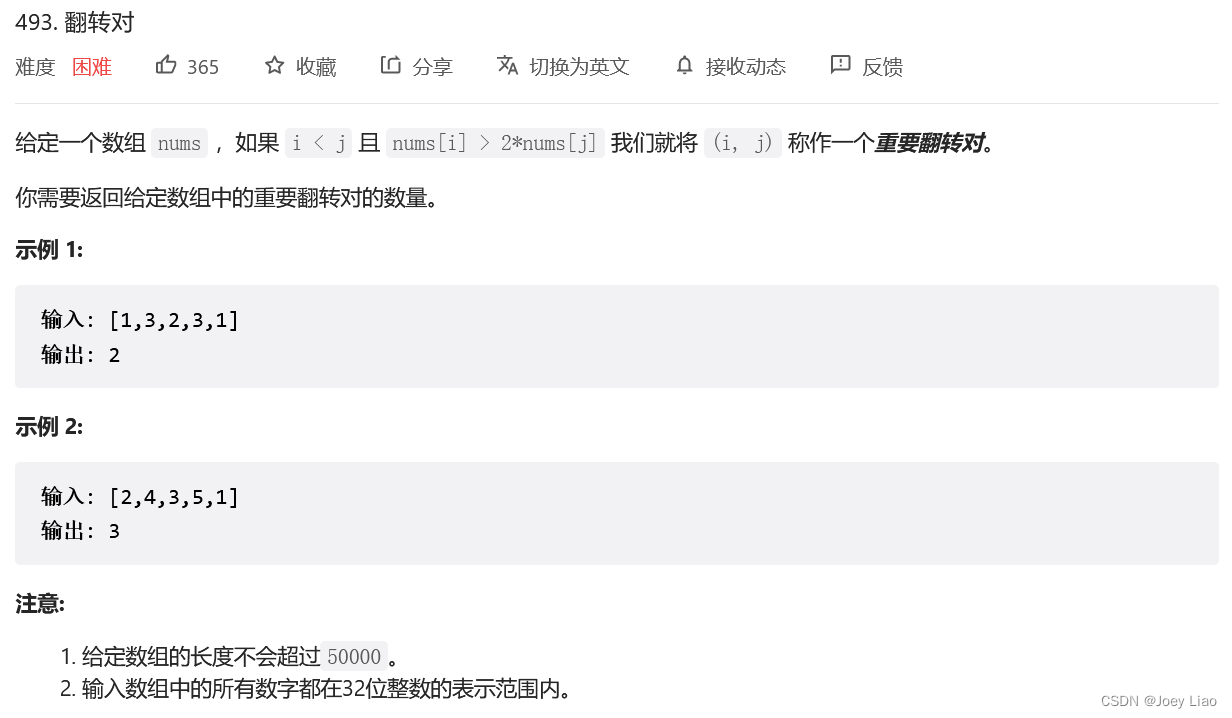
So of course, the idea of solving problems still needs to be merge Do something in the function , When nums[lo..mid] and nums[mid+1..hi] After sorting the two subarrays , about nums[lo..mid] Every element in nums[i], Go to nums[mid+1..hi] Look for qualified nums[j] That's it .

The code is as follows ：

class Solution {
    int res=0;
    int[] temp;//,doubleTemp;
    public int reversePairs(int[] nums) {
        int n=nums.length;
        temp=new int[n];
        mergeSort(nums,0,n-1);
        return res;
    }

    public void mergeSort(int[] nums,int left,int right){
        if(left==right){
            return;
        }
        int mid=left+(right-left)/2;
        mergeSort(nums,left,mid);
        mergeSort(nums,mid+1,right);
        merge(nums,left,mid,right);
    }
    public void merge(int[] nums,int left,int mid,int right){
        for(int i=left;i<=right;i++){
            temp[i]=nums[i];
        }
        ************************************************* The difference from ordinary merge sorting is here 
        int end=mid+1;
        for(int i=left;i<=mid;i++){
            while(end<=right&&(long)nums[i]>(long)nums[end]*2){
                end++;
            }
            res+=end-(mid+1);
        }
        ************************************************
        int i=left,j=mid+1;
        for(int k=left;k<=right;k++){
            if(i==mid+1){
                nums[k]=temp[j++];
            }else if(j==right+1){
                nums[k]=temp[i++];
            }else if(temp[i]<temp[j]){
                nums[k]=temp[i++];
            }else{
                nums[k]=temp[j++];
            }
        }
    }
}

The number of interval sums

Finally, let's look at a more difficult topic , Force to buckle 327 topic 「 The number of interval sums 」：

In short , The title lets you calculate the elements and fall on [lower, upper] The number of all subarrays in .

I won't talk about the violent solution of patting my head , Still nested for loop , Here we still talk about the efficient algorithm realized by merging and sorting .

First , To solve this problem, we need to quickly calculate the sum of subarrays , You need to create a prefix and array preSum To help us quickly calculate the interval sum .

I will continue to express this problem in the language of comparative Mathematics , The title lets you pass preSum Find an array count Array , bring ：

count[i] = COUNT(j) where lower <= preSum[j] - preSum[i] <= upper

Then please work out this count The sum of all elements in the array .

private int lower, upper;

public int countRangeSum(int[] nums, int lower, int upper) {
    this.lower = lower;
    this.upper = upper;
    //  Build prefixes and arrays , Be careful  int  It may spill over , use  long  Storage 
    long[] preSum = new long[nums.length + 1];
    for (int i = 0; i < nums.length; i++) {
        preSum[i + 1] = (long)nums[i] + preSum[i];
    }
    //  Merge and sort prefixes and arrays 
    sort(preSum);
    return count;
}

private long[] temp;

public void sort(long[] nums) {
    temp = new long[nums.length];
    sort(nums, 0, nums.length - 1);
}

private void sort(long[] nums, int lo, int hi) {
    if (lo == hi) {
        return;
    }
    int mid = lo + (hi - lo) / 2;
    sort(nums, lo, mid);
    sort(nums, mid + 1, hi);
    merge(nums, lo, mid, hi);
}

private int count = 0;

private void merge(long[] nums, int lo, int mid, int hi) {
    for (int i = lo; i <= hi; i++) {
        temp[i] = nums[i];
    }
    
    //  Add some private goods before merging ordered arrays （ This code will time out ）
    // for (int i = lo; i <= mid; i++) {
    //     for (int j = mid + 1; j <= hi; k++) {
    //         //  Look for qualified  nums[j]
    //         long delta = nums[j] - nums[i];
    //         if (delta <= upper && delta >= lower) {
    //             count++;
    //         }
    //     }
    // }
    
    //  Optimize efficiency 
    //  Maintain the left closed right open section  [start, end)  The elements in and  nums[i]  What's the difference  [lower, upper]  in 
    int start = mid + 1, end = mid + 1;
    for (int i = lo; i <= mid; i++) {
        //  If  nums[i]  The corresponding interval is  [start, end),
        //  that  nums[i+1]  The corresponding interval must move to the right as a whole , Similar to sliding window 
        while (start <= hi && nums[start] - nums[i] < lower) {
            start++;
        }
        while (end <= hi && nums[end] - nums[i] <= upper) {
            end++;
        }
        count += end - start;
    }

    //  Array double pointer technique , Merge two ordered arrays 
    int i = lo, j = mid + 1;
    for (int p = lo; p <= hi; p++) {
        if (i == mid + 1) {
            nums[p] = temp[j++];
        } else if (j == hi + 1) {
            nums[p] = temp[i++];
        } else if (temp[i] > temp[j]) {
            nums[p] = temp[j++];
        } else {
            nums[p] = temp[i++];
        }
    }
}

We are still merge The function adds some logic before merging ordered arrays , If you read the above Sliding window core frame , This efficiency optimization is a bit like maintaining a sliding window , Let the elements in the window and nums[i] The difference between [lower, upper] in .

For example, the merging sorting algorithm mentioned in this paper , Recursive sort Function is the traversal function of binary tree , and merge Functions are what you do on each node , Have you tasted something ？