当前位置:网站首页>3.2 Off-Policy Monte Carlo Methods & case study: Blackjack of off-Policy Evaluation
3.2 Off-Policy Monte Carlo Methods & case study: Blackjack of off-Policy Evaluation
2022-07-03 10:09:00 【Most appropriate commitment】
Catalog
Difference for two importance sampling in case of Infinite Variance
Background
In many cases, we are not able to find the examples in our specific policy. However, we could find examples in other policies with actions and states appearing in our policy.
What's more, in deterministic on-policy, we always have to compromise between exploring new states&actions ( in order to improve policies ) and choosing the fatal states&actions ( soft-greedy ). Therefore, the result is not optimal.
Therefore, If we could learn the policy  from the examples under the policy b, it will have many advantages.
from the examples under the policy b, it will have many advantages.
First, we could improve our policy in same examples in many loops.
Secondly, we could explore more even if our policy is deterministic.
Definition
![v_\pi(s) = E[G_t|S_t=s] \\=\ \sum_{a_t,s_{t+1},a_{t+1},...,s_{T-1},a_{T-1},s_T} Pr(A_t,S_{t+1},A_{t+1},...,S_T|S_t=s)(r_{t+1}+r_{t+2}+...+r_T) \\=\ \sum_{a_t,s_{t+1},a_{t+1},...,s_{T-1},a_{T-1},s_T} \pi(A_t|S_t)p(S_{t+1}|S_t,A_t)...p(S_T|S_{T-1},A_{T-1})(r_{t+1}+r_{t+2}+...+r_T)](http://img.inotgo.com/imagesLocal/202202/15/202202150539010291_13.gif)
and
![v_b(s) = E[G_t|S_t=s] \\=\ \sum_{a_t,s_{t+1},a_{t+1},...,s_{T-1},a_{T-1},s_T} Pr(A_t,S_{t+1},A_{t+1},...,S_T|S_t=s)(r_{t+1}+r_{t+2}+...+r_T) \\=\ \sum_{a_t,s_{t+1},a_{t+1},...,s_{T-1},a_{T-1},s_T} b(A_t|S_t)p(S_{t+1}|S_t,A_t)...p(S_T|S_{T-1},A_{T-1})(r_{t+1}+r_{t+2}+...+r_T)](http://img.inotgo.com/imagesLocal/202202/15/202202150539010291_3.gif)
Assume:

Therefore,
for oridnary importance sampling,

for weighed importance sampling,

difference for two importance sampling in case of Infinite Variance

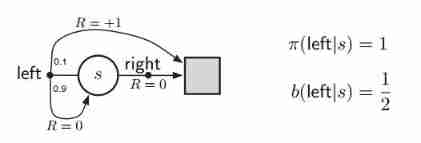
state: one state until terminal
action: left ; right
reward: R=1 when terminal
dynamic of environment: p(s,right,terminal) = 1 and R = 0 ; p(s,left,terminal)=0.1 and R = 1;
p(s,left,original state)=0.9 and R=0.
behavior policy: b(left|state)=b(right|state)=0.5
target policy: 
Code
## settings
import math
import numpy as np
import random
# visualization
import matplotlib
import matplotlib.pyplot as plt
from matplotlib.ticker import MultipleLocator
ORIGIN=0;
TERMINAL=1;
LEFT=0;
RIGHT=1
STATE={ORIGIN,TERMINAL}
Action={LEFT,RIGHT};
# probability of actions in the state (only one state)
target_policy = { LEFT: 1, RIGHT: 0};
behavior_policy = {LEFT:0.5, RIGHT:0.5};
# probability of current state, action, next state
p_s_a_s = np.zeros((2,2,2));
p_s_a_s[ORIGIN,LEFT,ORIGIN]=0.9;
p_s_a_s[ORIGIN,LEFT,TERMINAL]=0.1;
p_s_a_s[ORIGIN,RIGHT,ORIGIN]=0;
p_s_a_s[ORIGIN,RIGHT,TERMINAL]=1;
## functions
# check the reward
def get_reward(action,current_state):
if current_state == TERMINAL and action == LEFT:
return 1;
else:
return 0;
# get action from specific policy| in this case , the policy is b.
def get_action(b_policy):
p = np.array([b_policy[LEFT],b_policy[RIGHT]]);
return np.random.choice([LEFT,RIGHT],p=p.ravel());
# get state from chosen action:
def get_next_state(action):
p = np.array( [p_s_a_s[ORIGIN,action,ORIGIN],p_s_a_s[ORIGIN,action,TERMINAL]] );
return np.random.choice([ORIGIN,TERMINAL], p=p.ravel());
# set the sample:
class Agent_class( ):
def __init__(self):
self.state=ORIGIN;
self.state_set=[];
self.action_set=[];
def finish_sample(self):
self.state_set.append(self.state);
while(self.state==ORIGIN):
# get action from policy b
action = get_action(behavior_policy);
self.action_set.append(action);
# get next state from chosen action
next_state = get_next_state(action);
self.state = next_state
self.state_set.append(next_state);
## main programming and visualization
# 10 runs seperately
for num in range(0,10):
# settings for loop
Q_s_a_ordinary = np.zeros(2);
Q_n_ordinary=np.zeros(2);
Q_s_a_weigh = np.zeros(2);
Q_ratio_weigh = np.zeros(2,dtype = np.float64)
Q_ordinary_left=[]
Q_ordinary_right=[]
Q_weigh_left=[]
Q_weigh_right=[]
for loop in range(0,1000):
agent = Agent_class();
agent.finish_sample();
G = 0;
ratio = 1;
for i in range(1,len(agent.action_set)+1):
j=-i;
G += get_reward(agent.action_set[j],agent.state_set[j]);
ratio *= target_policy[ agent.action_set[j] ] / behavior_policy[ agent.action_set[j] ];
Q_s_a_ordinary[ agent.action_set[j] ] = Q_s_a_ordinary[ agent.action_set[j] ]* \
Q_n_ordinary[ agent.action_set[j] ] / (Q_n_ordinary[ agent.action_set[j] ]+1) \
+ ratio * G / (Q_n_ordinary[ agent.action_set[j] ]+1) ;
Q_ordinary_left.append(Q_s_a_ordinary[0]);
Q_ordinary_right.append(Q_s_a_ordinary[1]);
Q_n_ordinary[ agent.action_set[j] ] += 1;
if Q_s_a_weigh[ agent.action_set[j] ]==0 and ratio ==0:
continue;
Q_s_a_weigh[ agent.action_set[j] ] = Q_s_a_weigh[agent.action_set[j] ]* \
Q_ratio_weigh[ agent.action_set[j] ] / ( Q_ratio_weigh[ agent.action_set[j] ] + ratio ) \
+ ratio * G / ( Q_ratio_weigh[ agent.action_set[j] ] + ratio );
Q_weigh_left.append(Q_s_a_weigh[0]);
Q_weigh_right.append(Q_s_a_weigh[1]);
Q_ratio_weigh[agent.action_set[j] ] += ratio;
# visulation
plt.plot(Q_ordinary_left,lw=1,ms=1)
#plt.plot(Q_ordinary_right,'r^',lw=1,ms=1)
#plt.plot(Q_weigh_left,'b^',lw=1,ms=1)
#plt.plot(Q_weigh_right,'r^')
plt.axhline(y=1, c='k', ls='--', lw=1.5)
plt.axhline(y=2, c='k', ls='--', lw=1.5)
plt.ylim(0,3)
plt.ylabel('Monte Carlo estimate of q(s,a) with ordinary importance sampling')
plt.xlabel('updating number')
plt.show( )
Result

In ten runs, even after many loops, the estimate of q(state,left) does not converge because of the influence of the ever-chaning ratio  . But for weighed importance sampling, it won't influence like that.
. But for weighed importance sampling, it won't influence like that.
Moreover, because the target policy is deterministic, the estimate of q(state, right) is not updated.
??: Problem: If the policy is deterministic, how does off-policy update all state-value function?
Case Study: BlackJack
Code
## settings
import math
import numpy as np
import random
# visualization
import matplotlib
import matplotlib.pyplot as plt
from matplotlib.ticker import MultipleLocator
# state
# card scope
CARD_MINIMUM = 4;
CARD_MAXIMUM = 20;
CARD_TERMINAL = 21;
# rival's shown card
SHOWN_NUMBER_MINIMUM = 1;
SHOWN_NUMBER_MAXIMUM = 10;
# if we have usable Ace
ACE_ABLE = 1;
ACE_DISABLE = 0;
# action we can take
STICK = 0;
HIT = 1;
ACTION = [STICK,HIT];
# Reward of result
R_proceed = 0;
R_WIN = 1;
R_DRAW = 0;
R_LOSE = -1;
# loop number
LOOP =500000;
#policy
# our target policy stick at 20&21, or hit
pi_a_s = np.zeros((len(ACTION),CARD_MAXIMUM+1),dtype = np.float64)
for card in range(CARD_MINIMUM,CARD_MAXIMUM+1):
if card < 20:
pi_a_s[STICK,card] = 0;
pi_a_s[HIT,card] = 1;
else:
pi_a_s[STICK,card] = 1;
pi_a_s[HIT,card] = 0;
# rival policy stick on 17 or greater,
pi_rival_a_s = np.zeros((len(ACTION),CARD_MAXIMUM+1),dtype = np.float64)
for card in range(CARD_MINIMUM,CARD_MAXIMUM+1):
if card < 17:
pi_rival_a_s[STICK,card] = 0;
pi_rival_a_s[HIT,card] = 1;
else:
pi_rival_a_s[STICK,card] = 1;
pi_rival_a_s[HIT,card] = 0;
# behavior policy random
b_a_s = np.zeros((len(ACTION),CARD_MAXIMUM+1),dtype = np.float64)
for card in range(CARD_MINIMUM,CARD_MAXIMUM+1):
for act in ACTION:
b_a_s[act,card]= 1.0/len(ACTION);
# functions and class
#actions taken by policy and current sum_card
def get_action(sum_card,policy):
p=[];
for act in ACTION:
p.append(policy[act,sum_card]);
return np.random.choice(ACTION,p=p);
## set class for agent/rival to get sampling
class Agent_rival_class():
def __init__(self):
self.total_card=0;
self.card_set=[];
self.action_set=[];
self.last_action=HIT;
self.state = 'NORMAL&HIT';
self.showncard=0;
self.usable_ace=ACE_DISABLE;
for initial in range(0,2):
card = random.randint(1,14);
if card > 10:
card = 10;
if card == 1:
if self.usable_ace == ACE_ABLE:
card = 1;
else:
card = 11;
self.usable_ace = ACE_ABLE;
if initial == 0:
self.showncard = card;
if self.showncard == 11:
self.showncard = 1;
self.card_set.append(card);
self.total_card += card;
Agent_rival_class.check(self);
def check(self):
if self.total_card == 21:
self.state = 'TOP';
if self.total_card > 21:
self.state = 'BREAK';
if self.total_card < 21 and self.last_action == STICK:
self.state = 'NORMAL&STICK';
def behave(self,behave_policy):
self.last_action = get_action(self.total_card,behave_policy);
self.action_set.append(self.last_action);
if self.last_action == HIT:
card = random.randint(1,14);
if card > 10:
card = 10;
if card == 1:
if self.usable_ace == ACE_ABLE:
card = 1;
else:
card = 11;
self.usable_ace = ACE_ABLE;
self.total_card += card;
# make sure cards in set cards are from 1 to 10. without 11.
if card ==11:
self.card_set.append(1);
if self.total_card > 21 and self.usable_ace == ACE_ABLE:
self.total_card -= 10;
self.usable_ace = ACE_DISABLE;
Agent_rival_class.check(self);
# main programme
#rewards obtained
Q_s_a_ordinary = np.zeros((CARD_MAXIMUM+1,SHOWN_NUMBER_MAXIMUM+1,2,len(ACTION)),dtype = np.float64);
Q_n_ordinary=np.zeros((CARD_MAXIMUM+1,SHOWN_NUMBER_MAXIMUM+1,2,len(ACTION)));
V_s_ordinary = np.zeros((CARD_MAXIMUM+1,SHOWN_NUMBER_MAXIMUM+1,2),dtype = np.float64);
V_n_ordinary=np.zeros((CARD_MAXIMUM+1,SHOWN_NUMBER_MAXIMUM+1,2));
Q_s_a_weigh = np.zeros((CARD_MAXIMUM+1,SHOWN_NUMBER_MAXIMUM+1,2,len(ACTION)),dtype = np.float64);
Q_ratio_weigh = np.zeros((CARD_MAXIMUM+1,SHOWN_NUMBER_MAXIMUM+1,2,len(ACTION)),dtype = np.float64)
V_s_weigh = np.zeros((CARD_MAXIMUM+1,SHOWN_NUMBER_MAXIMUM+1,2),dtype = np.float64);
V_ratio_weigh = np.zeros((CARD_MAXIMUM+1,SHOWN_NUMBER_MAXIMUM+1,2),dtype = np.float64)
# choose the policy to decide
# off-policy ( BEHAVIOR_POLICY = b_a_s ) or
# on-policy ( BEHAVIOR_POLICY = pi_a_s )
BEHAVIOR_POLICY = pi_a_s;
TARGET_POLICY = pi_a_s;
for every_loop in range(0,LOOP):
S=[];
agent = Agent_rival_class();
rival = Agent_rival_class();
R_T = 0;
ratio = 1;
# obtain samples
# initialization of 21
if agent.state=='TOP' or rival.state=='TOP':
continue;
S.append([agent.total_card,rival.showncard,agent.usable_ace]);
while(agent.state=='NORMAL&HIT'):
# change the policy for behavioral policy
agent.behave(BEHAVIOR_POLICY);
S.append([agent.total_card,rival.showncard,agent.usable_ace]);
if agent.state == 'BREAK':
R_T = -1;
elif agent.state == 'TOP':
R_T = 1;
else:
while(rival.state=='NORMAL&HIT'):
rival.behave(pi_rival_a_s);
if rival.state == 'BREAK':
R_T = 1;
elif rival.state == 'TOP':
R_T = 0;
else:
if agent.total_card > rival.total_card:
R_T = 1;
elif agent.total_card < rival.total_card:
R_T = -1;
else:
R_T = 0;
# policy evaluation
G = R_T; # because R in the process is zero.
for i in range(1,len(agent.action_set)+1):
j = -i;
ratio *= TARGET_POLICY[ agent.action_set[j],S[j-1][0] ]/BEHAVIOR_POLICY[ agent.action_set[j],S[j-1][0] ];
# q_s_a for ordinary sample
Q_s_a_ordinary[S[j-1][0],S[j-1][1],S[j-1][2],agent.action_set[j]] = Q_s_a_ordinary[S[j-1][0],S[j-1][1],S[j-1][2],agent.action_set[j]] *\
Q_n_ordinary[S[j-1][0],S[j-1][1],S[j-1][2],agent.action_set[j]]/(Q_n_ordinary[S[j-1][0],S[j-1][1],S[j-1][2],agent.action_set[j]]+1) \
+ ratio*G/(Q_n_ordinary[S[j-1][0],S[j-1][1],S[j-1][2],agent.action_set[j]]+1);
Q_n_ordinary[S[j-1][0],S[j-1][1],S[j-1][2],agent.action_set[j]] +=1 ;
# V_s for ordinary sample
V_s_ordinary[S[j-1][0],S[j-1][1],S[j-1][2]] = V_s_ordinary[S[j-1][0],S[j-1][1],S[j-1][2]] *\
V_n_ordinary[S[j-1][0],S[j-1][1],S[j-1][2]]/(V_n_ordinary[S[j-1][0],S[j-1][1],S[j-1][2]]+1) \
+ ratio*G/(V_n_ordinary[S[j-1][0],S[j-1][1],S[j-1][2]]+1);
V_n_ordinary[S[j-1][0],S[j-1][1],S[j-1][2]] +=1 ;
# q_s_a for weighed sample
if ratio != 0 or Q_s_a_weigh[S[j-1][0],S[j-1][1],S[j-1][2],agent.action_set[j]] != 0:
Q_s_a_weigh[S[j-1][0],S[j-1][1],S[j-1][2],agent.action_set[j]] = Q_s_a_weigh[S[j-1][0],S[j-1][1],S[j-1][2],agent.action_set[j]] * \
Q_ratio_weigh[S[j-1][0],S[j-1][1],S[j-1][2],agent.action_set[j]] / (ratio + Q_ratio_weigh[S[j-1][0],S[j-1][1],S[j-1][2],agent.action_set[j]]) \
+ ratio * G / (ratio + Q_ratio_weigh[S[j-1][0],S[j-1][1],S[j-1][2],agent.action_set[j]]) ;
Q_ratio_weigh[S[j-1][0],S[j-1][1],S[j-1][2],agent.action_set[j]] += ratio;
# V_s for ordinary sample
if ratio != 0 or V_s_weigh[S[j-1][0],S[j-1][1],S[j-1][2]] != 0:
V_s_weigh[S[j-1][0],S[j-1][1],S[j-1][2]] = V_s_weigh[S[j-1][0],S[j-1][1],S[j-1][2]] * \
V_ratio_weigh[S[j-1][0],S[j-1][1],S[j-1][2]] / (ratio + V_ratio_weigh[S[j-1][0],S[j-1][1],S[j-1][2]]) \
+ ratio * G / (ratio + V_ratio_weigh[S[j-1][0],S[j-1][1],S[j-1][2]]) ;
V_ratio_weigh[S[j-1][0],S[j-1][1],S[j-1][2]] += ratio;
# visualization for Q_s_a and V_s for ordinary sample and weighed sample of off-policy and on-policy
#print(Q_s_a_ordinary[CARD_MINIMUM:CARD_MAXIMUM,SHOWN_NUMBER_MINIMUM:SHOWN_NUMBER_MAXIMUM,0,HIT])
fig, axes = plt.subplots(2,4,figsize=(30,50))
plt.subplots_adjust(left=None,bottom=None,right=None,top=None,wspace=0.5,hspace=0.5)
FONT_SIZE = 10;
xlabel=[]
ylabel=[]
for i in range(4,20+1):
ylabel.append(str(i))
for j in range(1,10+1):
xlabel.append(str(j))
# ordinary sample
#for 1,1 no Ace and stick
axes[0][0].set_xticks(range(0,10,1))
axes[0][0].set_xticklabels(xlabel)
axes[0][0].set_yticks(range(0,17,1) )
axes[0][0].set_yticklabels(ylabel)
axes[0][0].set_title('ordinary sample \n when no usable Ace and STICK',fontsize=FONT_SIZE)
im1 = axes[0][0].imshow(Q_s_a_ordinary[CARD_MINIMUM:CARD_MAXIMUM+1,SHOWN_NUMBER_MINIMUM:SHOWN_NUMBER_MAXIMUM+1,ACE_DISABLE,STICK],cmap=plt.cm.cool,vmin=-1, vmax=1)
#for 1,2 no Ace and hit
axes[0][1].set_xticks(range(0,10,1))
axes[0][1].set_xticklabels(xlabel)
axes[0][1].set_yticks(range(0,17,1) )
axes[0][1].set_yticklabels(ylabel)
axes[0][1].set_title('ordinary sample \n when no usable Ace and HIT',fontsize=FONT_SIZE)
im1 = axes[0][1].imshow(Q_s_a_ordinary[CARD_MINIMUM:CARD_MAXIMUM+1,SHOWN_NUMBER_MINIMUM:SHOWN_NUMBER_MAXIMUM+1,ACE_DISABLE,HIT],cmap=plt.cm.cool,vmin=-1, vmax=1)
#for 1,3 Ace and stick
axes[0][2].set_xticks(range(0,10,1))
axes[0][2].set_xticklabels(xlabel)
axes[0][2].set_yticks(range(0,17,1) )
axes[0][2].set_yticklabels(ylabel)
axes[0][2].set_title('ordinary sample \n when usable Ace and STICK',fontsize=FONT_SIZE)
im1 = axes[0][2].imshow(Q_s_a_ordinary[CARD_MINIMUM:CARD_MAXIMUM+1,SHOWN_NUMBER_MINIMUM:SHOWN_NUMBER_MAXIMUM+1,ACE_ABLE,STICK],cmap=plt.cm.cool,vmin=-1, vmax=1)
#for 1,4 Ace and hit
axes[0][3].set_xticks(range(0,10,1))
axes[0][3].set_xticklabels(xlabel)
axes[0][3].set_yticks(range(0,17,1) )
axes[0][3].set_yticklabels(ylabel)
axes[0][3].set_title('ordinary sample \n when usable Ace and HIT',fontsize=FONT_SIZE)
im1 = axes[0][3].imshow(Q_s_a_ordinary[CARD_MINIMUM:CARD_MAXIMUM+1,SHOWN_NUMBER_MINIMUM:SHOWN_NUMBER_MAXIMUM+1,ACE_ABLE,HIT],cmap=plt.cm.cool,vmin=-1, vmax=1)
# weighed sample
#for 2,1 no Ace and stick
axes[1][0].set_xticks(range(0,10,1))
axes[1][0].set_xticklabels(xlabel)
axes[1][0].set_yticks(range(0,17,1) )
axes[1][0].set_yticklabels(ylabel)
axes[1][0].set_title('weighed sample \n when no usable Ace and STICK',fontsize=FONT_SIZE)
im1 = axes[1][0].imshow(Q_s_a_weigh[CARD_MINIMUM:CARD_MAXIMUM+1,SHOWN_NUMBER_MINIMUM:SHOWN_NUMBER_MAXIMUM+1,ACE_DISABLE,STICK],cmap=plt.cm.cool,vmin=-1, vmax=1)
#for 2,2 no Ace and hit
axes[1][1].set_xticks(range(0,10,1))
axes[1][1].set_xticklabels(xlabel)
axes[1][1].set_yticks(range(0,17,1) )
axes[1][1].set_yticklabels(ylabel)
axes[1][1].set_title('weighed sample \n when no usable Ace and HIT',fontsize=FONT_SIZE)
im1 = axes[1][1].imshow(Q_s_a_weigh[CARD_MINIMUM:CARD_MAXIMUM+1,SHOWN_NUMBER_MINIMUM:SHOWN_NUMBER_MAXIMUM+1,ACE_DISABLE,HIT],cmap=plt.cm.cool,vmin=-1, vmax=1)
#for 2,3 Ace and stick
axes[1][2].set_xticks(range(0,10,1))
axes[1][2].set_xticklabels(xlabel)
axes[1][2].set_yticks(range(0,17,1) )
axes[1][2].set_yticklabels(ylabel)
axes[1][2].set_title('weighed sample \n when usable Ace and STICK',fontsize=FONT_SIZE)
im1 = axes[1][2].imshow(Q_s_a_weigh[CARD_MINIMUM:CARD_MAXIMUM+1,SHOWN_NUMBER_MINIMUM:SHOWN_NUMBER_MAXIMUM+1,ACE_ABLE,STICK],cmap=plt.cm.cool,vmin=-1, vmax=1)
#for 2,4 Ace and hit
axes[1][3].set_xticks(range(0,10,1))
axes[1][3].set_xticklabels(xlabel)
axes[1][3].set_yticks(range(0,17,1) )
axes[1][3].set_yticklabels(ylabel)
axes[1][3].set_title('weighed sample \n when usable Ace and HIT',fontsize=FONT_SIZE)
im1 = axes[1][3].imshow(Q_s_a_weigh[CARD_MINIMUM:CARD_MAXIMUM+1,SHOWN_NUMBER_MINIMUM:SHOWN_NUMBER_MAXIMUM+1,ACE_ABLE,HIT],cmap=plt.cm.cool,vmin=-1, vmax=1)
fig = axes[0][0].figure
fig.suptitle('state-action function',fontsize=15)
fig.colorbar(im1,ax=axes.ravel().tolist())
plt.show()
# for value function
fig2, axes2 = plt.subplots(2,2,figsize=(30,50))
# ordinary sample
#for 1,1 no Ace
axes2[0][0].set_xticks(range(0,10,1))
axes2[0][0].set_xticklabels(xlabel)
axes2[0][0].set_yticks(range(0,17,1) )
axes2[0][0].set_yticklabels(ylabel)
axes2[0][0].set_title('ordinary sample \n when no usable Ace ',fontsize=FONT_SIZE)
im2 = axes2[0][0].imshow(V_s_ordinary[CARD_MINIMUM:CARD_MAXIMUM+1,SHOWN_NUMBER_MINIMUM:SHOWN_NUMBER_MAXIMUM+1,ACE_DISABLE],cmap=plt.cm.cool,vmin=-1, vmax=1)
#for 1,2 Ace
axes2[0][1].set_xticks(range(0,10,1))
axes2[0][1].set_xticklabels(xlabel)
axes2[0][1].set_yticks(range(0,17,1) )
axes2[0][1].set_yticklabels(ylabel)
axes2[0][1].set_title('ordinary sample \n when usable Ace ',fontsize=FONT_SIZE)
axes2[0][1].imshow(V_s_ordinary[CARD_MINIMUM:CARD_MAXIMUM+1,SHOWN_NUMBER_MINIMUM:SHOWN_NUMBER_MAXIMUM+1,ACE_ABLE],cmap=plt.cm.cool,vmin=-1, vmax=1)
# weighed sample
#for 2,1 no Ace
axes2[1][0].set_xticks(range(0,10,1))
axes2[1][0].set_xticklabels(xlabel)
axes2[1][0].set_yticks(range(0,17,1) )
axes2[1][0].set_yticklabels(ylabel)
axes2[1][0].set_title('weighed sample \n when no usable Ace',fontsize=FONT_SIZE)
axes2[1][0].imshow(V_s_weigh[CARD_MINIMUM:CARD_MAXIMUM+1,SHOWN_NUMBER_MINIMUM:SHOWN_NUMBER_MAXIMUM+1,ACE_DISABLE],cmap=plt.cm.cool,vmin=-1, vmax=1)
#for 2,2 Ace
axes2[1][1].set_xticks(range(0,10,1))
axes2[1][1].set_xticklabels(xlabel)
axes2[1][1].set_yticks(range(0,17,1) )
axes2[1][1].set_yticklabels(ylabel)
axes2[1][1].set_title('weighed sample \n when usable Ace ',fontsize=FONT_SIZE)
axes2[1][1].imshow(V_s_weigh[CARD_MINIMUM:CARD_MAXIMUM+1,SHOWN_NUMBER_MINIMUM:SHOWN_NUMBER_MAXIMUM+1,ACE_ABLE],cmap=plt.cm.cool,vmin=-1, vmax=1)
fig2.suptitle('value function',fontsize=15)
fig2.colorbar(im2,ax=axes2.ravel().tolist())
plt.show()Result:
off-policy:
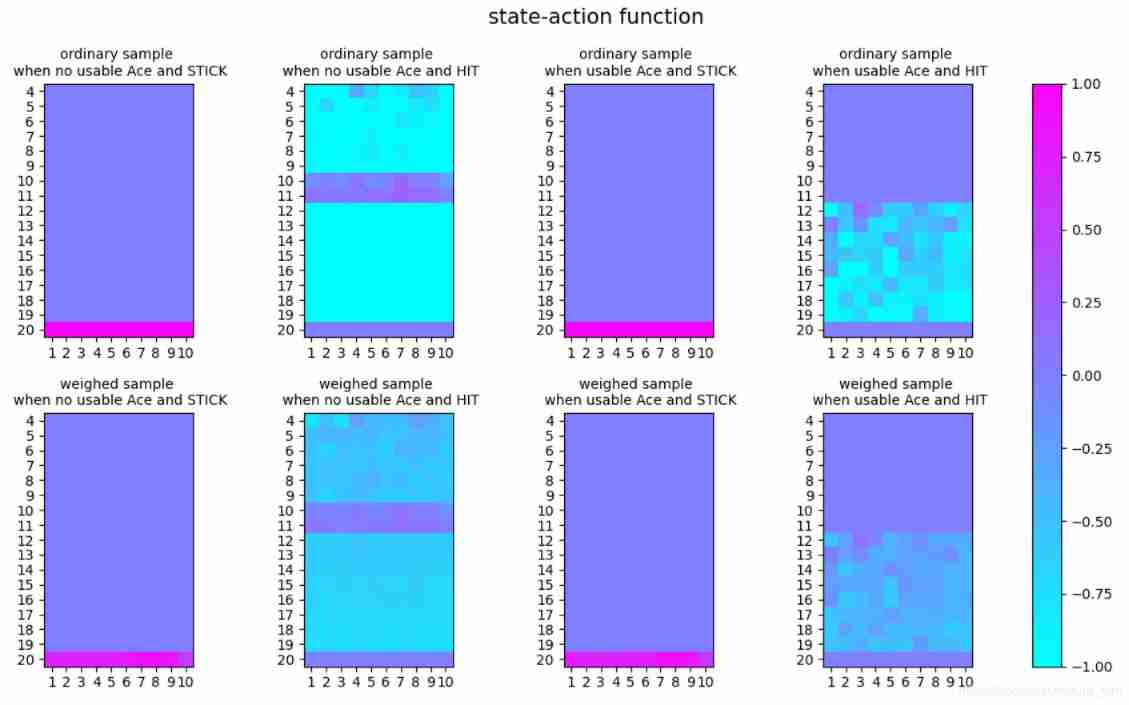

on-policy:


In this result, we could see the little difference between ordinary sample and weighed sample.
In off-policy and on-policy, there is no difference. And the on-policy result is more like weighed sample in off-policy.
边栏推荐
- My openwrt learning notes (V): choice of openwrt development hardware platform - mt7688
- 2020-08-23
- Not many people can finally bring their interests to college graduation
- El table X-axis direction (horizontal) scroll bar slides to the right by default
- LeetCode - 1172 餐盘栈 (设计 - List + 小顶堆 + 栈))
- 4G module IMEI of charging pile design
- Crash工具基本使用及实战分享
- My notes on intelligent charging pile development (II): overview of system hardware circuit design
- Leetcode interview question 17.20 Continuous median (large top pile + small top pile)
- Assignment to '*' form incompatible pointer type 'linkstack' {aka '*'} problem solving
猜你喜欢
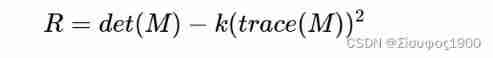
Opencv Harris corner detection

CV learning notes - Stereo Vision (point cloud model, spin image, 3D reconstruction)

QT self drawing button with bubbles

Yocto technology sharing phase IV: customize and add software package support
Basic knowledge of communication interface

Windows下MySQL的安装和删除
LeetCode - 919. Full binary tree inserter (array)

My notes on the development of intelligent charging pile (III): overview of the overall design of the system software
![[combinatorics] Introduction to Combinatorics (combinatorial idea 3: upper and lower bound approximation | upper and lower bound approximation example Remsey number)](/img/19/5dc152b3fadeb56de50768561ad659.jpg)
[combinatorics] Introduction to Combinatorics (combinatorial idea 3: upper and lower bound approximation | upper and lower bound approximation example Remsey number)
CV learning notes - camera model (Euclidean transformation and affine transformation)
随机推荐
Drive and control program of Dianchuan charging board for charging pile design
LeetCode - 1670 设计前中后队列(设计 - 两个双端队列)
Qcombox style settings
Emballage automatique et déballage compris? Quel est le principe?
LeetCode - 1172 餐盘栈 (设计 - List + 小顶堆 + 栈))
Dynamic layout management
Positive and negative sample division and architecture understanding in image classification and target detection
Opencv feature extraction - hog
Toolbutton property settings
01 business structure of imitation station B project
2. Elment UI date selector formatting problem
Retinaface: single stage dense face localization in the wild
Replace the files under the folder with sed
yocto 技術分享第四期:自定義增加軟件包支持
RESNET code details
使用密钥对的形式连接阿里云服务器
(1) 什么是Lambda表达式
STM32 running lantern experiment - library function version
CV learning notes - scale invariant feature transformation (SIFT)
Tensorflow built-in evaluation
