当前位置:网站首页>CV learning notes - camera model (Euclidean transformation and affine transformation)
CV learning notes - camera model (Euclidean transformation and affine transformation)
2022-07-03 10:07:00 【Moresweet cat】
Camera model
1. Camera model principle
1. Camera imaging
Camera imaging is a small hole imaging model , Map the three-dimensional space object in real life to the two-dimensional imaging plane , And then generate a two-dimensional image .
![[ Failed to transfer the external chain picture , The origin station may have anti-theft chain mechanism , It is suggested to save the pictures and upload them directly (img-DEGq4FLV-1637041595381)(./imgs/image-20211114135810896.png)]](/img/39/b4b0ec2b8be1cf730d13c05e49a07e.jpg)
Coordinate system in camera model :
- World coordinate system Pw(Xw, Yw, Zw): Coordinate system corresponding to the real and objective three-dimensional world , Also known as the objective coordinate system , Represent the position coordinates of the object in the real world . The world coordinate system changes with the size and position of the object , Units are generally units of length .
- Camera coordinate system PO(x, y, z): Corresponding to the coordinate system with the optical center of the camera as the origin , It is parallel to the image x and y Direction is x Axis y Axis ,z The axis is parallel to the optical axis , The unit is also the unit of length .
- Image physical coordinate system P’(x’, y’): Corresponding to the coordinate system with the intersection of the main optical axis and the image plane as the coordinate origin , The unit is still the unit of length .
- Image pixel coordinate system P(u, v): Corresponding to the coordinate system with the vertex of the image as the coordinate origin ,u and v The direction of is parallel to x’ and y’ Direction , Unit is pixel
![[ Failed to transfer the external chain picture , The origin station may have anti-theft chain mechanism , It is suggested to save the pictures and upload them directly (img-dzVaIQd1-1637041595384)(./imgs/image-20211114141130252.png)]](/img/51/8b4c02a22041d71fbc119236815231.jpg)
Camera imaging process :
2. Coordinate transformation
European transformation : Objects in any three-dimensional space , Can be expressed in three-dimensional coordinate system , That is, the point of an object in real space , The coordinates are different in different coordinate systems , Because the base is different , So a fixed point , Coordinates in a coordinate system , If you convert to another coordinate system , So that another coordinate system can determine this position , You need to use Euclidean transformation . The transformation from any coordinate system to another coordinate system can be completed by rotation and Translation .
Translation transformation & Rotation transformation & Homogeneous coordinates :
Translation transformation It refers to the transformation of the coordinate systems of both sides for a finite number of times translation Sure coincidence , For example, the high hat is directly above the face , In this way, the central coordinate system of the face is converted to the central coordinate system of the high hat , Just translate and transform the coordinate origin upward , There is no rotation offset of the coordinate axis , The translation transformation in linear algebra is the transformation of the position in the spatial coordinate system , It is customary to use O Vector representation of , By adding constants to vectors , Multiple translation transformations can be realized by adding vectors directly . Translation transformation is relatively simple and easy to understand , The rotation transformation is more complex , It can be extended to three-dimensional Cartesian coordinate system through two-dimensional coordinate rotation transformation , For rigid bodies in space , There are six degrees of freedom , Around the xyz There are three degrees of freedom of rotation , And in the two-dimensional plane , Only rotate about the axis of the vertical plane , That is, there can only be one degree of freedom , Then for the three-dimensional coordinate system, you can write 3×3 Of R matrix , Write it as a rotation matrix
![[ Failed to transfer the external chain picture , The origin station may have anti-theft chain mechanism , It is suggested to save the pictures and upload them directly (img-sIJZU6A8-1637041595386)(./imgs/image-20211116123138089.png)]](/img/7d/59a3793ca39734e66e00b28950c803.jpg)
The above formula means from B Coordinate system conversion to A Each column of sub vectors in the rotation matrix of the coordinate system , The equivalent is B The coordinate axis unit vector of the coordinate system is A The representation in the coordinate system . It is not difficult to find that this rotation matrix is an orthogonal unit matrix , Therefore, the following inference :
![[ Failed to transfer the external chain picture , The origin station may have anti-theft chain mechanism , It is suggested to save the pictures and upload them directly (img-tW190L2w-1637041595387)(./imgs/image-20211116123357528.png)]](/img/4e/a5a6379f4d014920664a02c50b5c04.jpg)
The above formula explains , Every row of the matrix is A The coordinate axis of the coordinate system is B The representation in the coordinate system . The formula of rotation transformation is as follows :
![[ Failed to transfer the external chain picture , The origin station may have anti-theft chain mechanism , It is suggested to save the pictures and upload them directly (img-inzoW6ly-1637041595388)(./imgs/image-20211116123625208.png)]](/img/27/94b3ac5a5a96583c06716270b91628.jpg)
Continuous rotation transformation can only be achieved by matrix multiplication . When the rotation translation transformation occurs at the same time , Introduce the concept of homogeneous coordinate transformation ;
![[ Failed to transfer the external chain picture , The origin station may have anti-theft chain mechanism , It is suggested to save the pictures and upload them directly (img-pn3xhoty-1637041595390)(./imgs/clip_image002.jpg)]](/img/4f/acb8852067a812cc9b05933371d19c.jpg)
From the above conclusion, it is not difficult to deduce this transformation process , If this process is represented by a matrix , It's a lot simpler , Homogeneous coordinate transformation matrix also came into being , The transformation process of the above figure is equivalent to the following expression :
![[ Failed to transfer the external chain picture , The origin station may have anti-theft chain mechanism , It is suggested to save the pictures and upload them directly (img-9PiJxnCB-1637041595392)(./imgs/image-20211116123937788.png)]](/img/8b/0f1d1f56da73a14554fba1cad17334.jpg)
T Matrix is the homogeneous coordinate transformation matrix in this transformation , Homogeneous coordinate transformation matrix T It's a fourth-order square matrix , It can represent rotation transformation and translation transformation at the same time , The formula of homogeneous coordinate transformation matrix is expressed as follows :
![[ Failed to transfer the external chain picture , The origin station may have anti-theft chain mechanism , It is suggested to save the pictures and upload them directly (img-krBrsXjf-1637041595393)(./imgs/image-20211116124053414.png)]](/img/5c/c917a5b91a349309fa5264dda68495.jpg)
Simplify the angle sign of the above derivation process , for instance :
If vector a Perform two Euclidean transformations , The rotation and translation are R1,t1 and R2,t2, Get... Separately :
b = R1*a + t1; c = R2*b + t2; c = R2*(R1*a + t1) + t2
![[ Failed to transfer the external chain picture , The origin station may have anti-theft chain mechanism , It is suggested to save the pictures and upload them directly (img-STam15ri-1637041595395)(./imgs/image-20211116124949731.png)]](/img/a3/d797cd4866344a8405fc8d11b94634.jpg)
World coordinate system to camera coordinate system :
The rotation matrix is no exception in the transformation from the world coordinate system to the camera coordinate system R Peaceshift matrix t, The relationship is expressed as :
![[ Failed to transfer the external chain picture , The origin station may have anti-theft chain mechanism , It is suggested to save the pictures and upload them directly (img-tqf2QbFV-1637041595396)(./imgs/image-20211116125309891.png)]](/img/2f/4c9f2a06fadfd4b1f5b1ed9a03c86c.jpg)
Camera coordinate system to image physical coordinate system :
- principle : Similar triangles
![[ Failed to transfer the external chain picture , The origin station may have anti-theft chain mechanism , It is suggested to save the pictures and upload them directly (img-WiziuuLD-1637041595398)(./imgs/image-20211116125508932.png)]](/img/8b/b6b275c5395a7b228e140f0aef8010.jpg)
![[ Failed to transfer the external chain picture , The origin station may have anti-theft chain mechanism , It is suggested to save the pictures and upload them directly (img-3n3XYeQR-1637041595399)(./imgs/image-20211116125549226.png)]](/img/c2/548809f8c851026eff44e40b6052a3.jpg)
- The matrix is expressed as :f For focus
![[ Failed to transfer the external chain picture , The origin station may have anti-theft chain mechanism , It is suggested to save the pictures and upload them directly (img-kgZFpeVi-1637041595401)(./imgs/image-20211116125922909.png)]](/img/d1/9d7f5f0dc2b57167d177af27834244.jpg)
Image physical coordinate system to image pixel coordinate system :
- principle : Coordinate offset (dx、dy Express x and y How many length units does a pixel in the direction occupy ,dx、dy It could be a decimal )
![[ Failed to transfer the external chain picture , The origin station may have anti-theft chain mechanism , It is suggested to save the pictures and upload them directly (img-5zcFeD8F-1637041595402)(./imgs/image-20211116130257426.png)]](/img/72/4a47d21ed3b87369cae676d721f950.jpg)
![[ Failed to transfer the external chain picture , The origin station may have anti-theft chain mechanism , It is suggested to save the pictures and upload them directly (img-kssDeKW0-1637041595405)(./imgs/image-20211116130324834.png)]](/img/34/9ba8ec2f1b631ebaafc97872ac6f3b.jpg)
- Homogeneous coordinates represent :
![[ Failed to transfer the external chain picture , The origin station may have anti-theft chain mechanism , It is suggested to save the pictures and upload them directly (img-yZgNFYBP-1637041595406)(./imgs/image-20211116130551385.png)]](/img/5a/61cb21eba93b494094d819e22e14cd.jpg)
Continuous Euclidean transformation from camera coordinate system to image pixel coordinate system :
![[ Failed to transfer the external chain picture , The origin station may have anti-theft chain mechanism , It is suggested to save the pictures and upload them directly (img-L6TFCxia-1637041595407)(./imgs/image-20211116130721117.png)]](/img/e1/1ba88d3c271e1986033e89c71e895b.jpg)
World coordinate system to image pixel coordinate system :
- Derivation process :
![[ Failed to transfer the external chain picture , The origin station may have anti-theft chain mechanism , It is suggested to save the pictures and upload them directly (img-7b3kSHN4-1637041595408)(./imgs/image-20211116130944386.png)]](/img/f0/a7d1ac7371570633a668ae70267382.jpg)
![[ Failed to transfer the external chain picture , The origin station may have anti-theft chain mechanism , It is suggested to save the pictures and upload them directly (img-KHbmlGmw-1637041595409)(./imgs/image-20211116131023041.png)]](/img/4a/f5257a1b487dad9426ba730fe7d814.jpg)
- Conclusion :
![[ Failed to transfer the external chain picture , The origin station may have anti-theft chain mechanism , It is suggested to save the pictures and upload them directly (img-dXGjUqCT-1637041595410)(./imgs/image-20211116131109134.png)]](/img/ce/fb0e0383f106310e7dc6547af95cf4.jpg)
2. Lens distortion
1. Lens distortion
Due to the deviation of manufacturing accuracy and assembly process , The finished lens often produces distortion , Cause distortion of the original image . Lens distortion is divided into radial distortion and tangential distortion .
![[ Failed to transfer the external chain picture , The origin station may have anti-theft chain mechanism , It is suggested to save the pictures and upload them directly (img-EASvNKiP-1637041595411)(./imgs/image-20211116131523568.png)]](/img/5d/93fc26150aaac6a7241ec1f7343c45.jpg)
2. Radial distortion
- reason : The distortion caused by the shape of the lens is called radial distortion , Schematic diagram of point displacement after radial distortion of lens :
![[ Failed to transfer the external chain picture , The origin station may have anti-theft chain mechanism , It is suggested to save the pictures and upload them directly (img-FPFTjLei-1637041595412)(./imgs/image-20211116131711931.png)]](/img/b1/2f3d52ab4b542a6419fbdfdb70fed3.jpg)
Occipital distortion
![[ Failed to transfer the external chain picture , The origin station may have anti-theft chain mechanism , It is suggested to save the pictures and upload them directly (img-uTXee5a2-1637041595413)(./imgs/image-20211116131811689.png)]](/img/09/a4a81671e6506a077403113e4aae87.jpg)
Barrel distortion
![[ Failed to transfer the external chain picture , The origin station may have anti-theft chain mechanism , It is suggested to save the pictures and upload them directly (img-9Ghy2CWH-1637041595414)(./imgs/image-20211116131848978.png)]](/img/e6/f344a9785cf89516d1b1d08d8787ba.jpg)
3. Tangential distortion
- reason : Tangential distortion is due to the lens itself and the camera sensor plane ( Imaging plane ) Or the image plane is not parallel .( Mostly due to the installation deviation of the lens pasted on the lens module )
![[ Failed to transfer the external chain picture , The origin station may have anti-theft chain mechanism , It is suggested to save the pictures and upload them directly (img-8LeygAeL-1637041595415)(./imgs/image-20211116132221556.png)]](/img/21/b36d824dcf1ebd1ca49f86a371d08f.jpg)
4. Distortion correction
Method :
Radial distortion and tangential distortion models have 5 Distortion parameters , stay Opencv They are arranged in a 5*1 Matrix , Include in turn k1、k2、p1、p2、k3( this 5 The first parameter is the camera parameter that needs to be determined in camera calibration 5 Distortion coefficients ), Often defined as Mat Matrix form
Mat distCoeffs = Mat(1.5, CV_32FC1, Scalar::all(0));Get this 5 After a parameter , The distortion of the image caused by lens distortion can be corrected .
![[ Failed to transfer the external chain picture , The origin station may have anti-theft chain mechanism , It is suggested to save the pictures and upload them directly (img-FSfPy3h4-1637041595416)(./imgs/image-20211116132730949.png)]](/img/30/5d30ace6eede245ea308c2b716b349.jpg)
![[ Failed to transfer the external chain picture , The origin station may have anti-theft chain mechanism , It is suggested to save the pictures and upload them directly (img-qiAoMd4g-1637041595417)(./imgs/image-20211116132801198.png)]](/img/85/958837cf7ef55bf74ab4bb894e1fcd.jpg)
3. Perspective transformation
1. Definition
Perspective transformation is also called projection mapping (Projective Mapping), It is to project a picture from the original plane to a new viewing plane (Viewing Plane) The process of .
2. Purpose
Real objects are straight edges, which may be oblique lines in the picture , This oblique line can be transformed into a straight line through perspective transformation .
3. And affine transformation
Affine transformation is a special case of perspective transformation , Affine transformation (Affine Transformation or Affine Map) It refers to a linear transformation and a translation of an image from a vector space in geometry , The process of transforming to another vector space .
![[ Failed to transfer the external chain picture , The origin station may have anti-theft chain mechanism , It is suggested to save the pictures and upload them directly (img-92pEaRFO-1637041595418)(./imgs/image-20211116133853212.png)]](/img/ca/09c6327861aad2e743a1937c01e575.jpg)
4. The transformation process
- Change the formula :
![[ Failed to transfer the external chain picture , The origin station may have anti-theft chain mechanism , It is suggested to save the pictures and upload them directly (img-RQUxgcHB-1637041595419)(./imgs/image-20211116133953678.png)]](/img/b5/e8c3e9e821174f9343e57fb2b70870.jpg)
In the following formula X,Y Is the coordinates of the original picture ( Upper type x,y), Corresponding to the transformed picture coordinates (X’;Y’;Z’) among Z’=1:
![[ Failed to transfer the external chain picture , The origin station may have anti-theft chain mechanism , It is suggested to save the pictures and upload them directly (img-KjZHhO4I-1637041595420)(./imgs/image-20211116134103712.png)]](/img/37/3a62942b84e8c929b5a4c513aa86e1.jpg)
In a general way , We make a33=1, Expand the above formula , Get a point :
![[ Failed to transfer the external chain picture , The origin station may have anti-theft chain mechanism , It is suggested to save the pictures and upload them directly (img-ehyyWqRw-1637041595421)(./imgs/image-20211116134232783.png)]](/img/23/1c1233e40f4411bd74942c123420e0.jpg)
![[ Failed to transfer the external chain picture , The origin station may have anti-theft chain mechanism , It is suggested to save the pictures and upload them directly (img-BbqPkWD7-1637041595422)(./imgs/image-20211116134424612.png)]](/img/f2/a740abfd5cbf1cf05d450bf581e6cf.jpg)
Personal study notes , Just learn to communicate , Reprint please indicate the source !
边栏推荐
- Working mode of 80C51 Serial Port
- LeetCode - 508. 出现次数最多的子树元素和 (二叉树的遍历)
- Serial port programming
- Google browser plug-in recommendation
- RESNET code details
- QT is a method of batch modifying the style of a certain type of control after naming the control
- YOLO_ V1 summary
- (2) New methods in the interface
- Tensorflow2.0 save model
- Blue Bridge Cup for migrant workers majoring in electronic information engineering
猜你喜欢

Leetcode - 933 number of recent requests

RESNET code details

Yocto technology sharing phase IV: customize and add software package support

应用最广泛的8位单片机当然也是初学者们最容易上手学习的单片机
Leetcode - 1670 design front, middle and rear queues (Design - two double ended queues)

Seven sorting of ten thousand words by hand (code + dynamic diagram demonstration)
Opencv notes 17 template matching
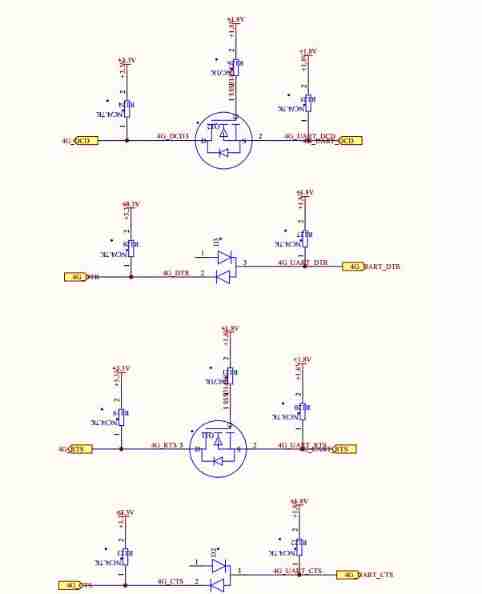
My notes on intelligent charging pile development (II): overview of system hardware circuit design

I think all friends should know that the basic law of learning is: from easy to difficult

MySQL root user needs sudo login
随机推荐
Positive and negative sample division and architecture understanding in image classification and target detection
Vgg16 migration learning source code
[untitled] proteus simulation of traffic lights based on 89C51 Single Chip Microcomputer
STM32 general timer 1s delay to realize LED flashing
Crash工具基本使用及实战分享
Application of external interrupts
After clicking the Save button, you can only click it once
Timer and counter of 51 single chip microcomputer
My notes on intelligent charging pile development (II): overview of system hardware circuit design
LeetCode 面试题 17.20. 连续中值(大顶堆+小顶堆)
Opencv note 21 frequency domain filtering
Open Euler Kernel Technology Sharing - Issue 1 - kdump Basic Principles, use and Case Introduction
自動裝箱與拆箱了解嗎?原理是什麼?
01 business structure of imitation station B project
LeetCode - 705 设计哈希集合(设计)
An executable binary file contains more than machine instructions
2312、卖木头块 | 面试官与狂徒张三的那些事(leetcode,附思维导图 + 全部解法)
Development of intelligent charging pile (I): overview of the overall design of the system
getopt_ Typical use of long function
QT setting suspension button