当前位置:网站首页>函数递归1.0
函数递归1.0
2022-07-31 12:10:00 【林深方见鹿】
首先我们简单来认识一下什么是递归,递归就是一个过程或函数在其定义或说明中有直接或者间接调用自身的一种方法,递归的主要思考方式在于把大事化小。
递归有两个必要条件:存在限制条件,当满足限制条件时,递归便会停止;每次递归调用都会越来越接近这个限制条件。
举例1:
输入一个无符号整形数,按照顺序打印每一位数字。比如输入1234,打印1 2 3 4.
下面来展示一下我的思考过程:
如果这个数只有个位数,那么直接打印就可以了,如果大于九,就需要我们想办法来解决了,怎么解决呢?我们要得到单独的一个数字,最简单的办法就是直接除以10,然后再对10取模,就得到了单独的一位数,想到这一步,就继续想着要找到一个合适的途径去实现,递归是一种很好的方式,通过递归调用,调用到最接近限制条件,到达最底层,然后再一步步返回上一层,回到最顶层,最后得到我们想要的结果。
我们来看一下程序:
#include<stdio.h>
void print(int n)
{
if (n > 9)
print(n / 10);
printf("%d ", n%10 );
}
int main()
{
int num;
printf("请输入一个整型值:\n");
scanf("%d", &num);
print(num);
return 0;
}运行结果:

举例2:
用递归求阶乘。
我们知道,0和1的阶乘等于1,当n大于1时,n的阶乘等于n-1的阶乘乘以n,所以我们就可以借助递归来实现求阶乘。
//求n的阶乘
#include<stdio.h>
int factorial(int n)
{
if (n <= 1)
return 1;
else
return n*factorial(n - 1);
}
int main()
{
int n = 5;
int res = factorial(n);
printf("%d \n", res);
return 0;
}运行结果:

举例3:
求第n个斐波那契数(不考虑溢出)
//求第n个斐波那契数(不考虑溢出)
#include<stdio.h>
int fib(int n)
{
if (n <= 2)
return 1;
else
return (fib(n - 1) + fib(n - 2));
}
int main()
{
int n = 7;
int res = fib(7);
printf("%d ", res);
return 0;
}运行结果:

通过上面的例子,我们可以得到以下结论:
递归通常把一个复杂的问题简单化,它通过层层转化,将大型复杂的问题层层转化为一个相似的较小规模的问题来求解,递归策略只需要少量的程序就可以描述出解题过程中所需要的多次重复计算,大大的减少了程序的代码量。
边栏推荐
- Docker搭建Mysql主从复制
- Use Excel to read data exposed by SAP ABAP CDS View through ODBC
- [core]-ARMV7-A、ARMV8-A、ARMV9-A 架构简介「建议收藏」
- 在 Excel 里使用 ODBC 读取 SAP BTP 平台上 CDS view 的数据
- 初识QEMU
- 给你一个大厂面试的机会,你能面试上吗?进来看看!
- 订song餐系统
- MySQL row-level locks (row locks, adjacent key locks, gap locks)
- lotus-local-net 2k v1.17.0-rc4
- 如何正确地把服务器端返回的文件二进制流写入到本地保存成文件
猜你喜欢
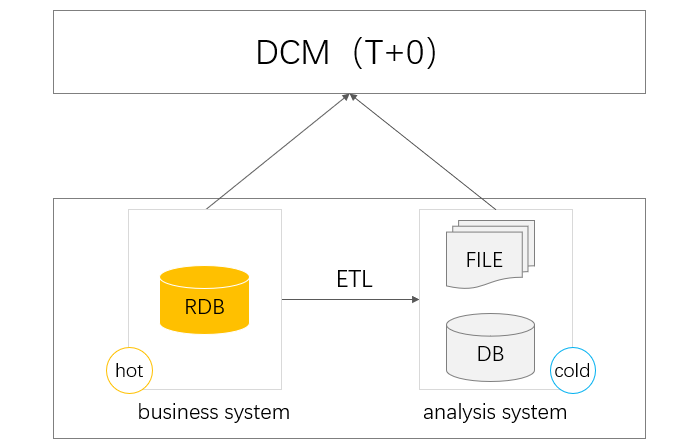
DCM 中间件家族迎来新成员
Docker build Mysql master-slave replication
The latest MySql installation teaching, very detailed
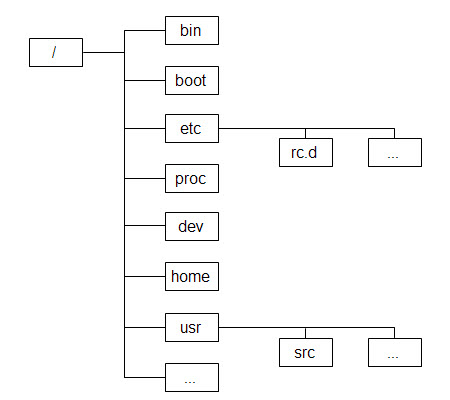
chroot命令
apisix-Getting Started

St. Regis Takeaway Project: New dishes and dishes paged query

Docker搭建Mysql主从复制
Full GC (Ergonomics)排查分析

纷享销客罗旭对话元气森林黄晓枫:零售数字化的终点不是创新,而是数据

file contains vulnerabilities
随机推荐
双非一本进字节了!!纯干货分享
[Shader] Shader official example [easy to understand]
给你一个大厂面试的机会,你能面试上吗?进来看看!
Is the working process of the belt you know the story - actionreducerstore
The latest MySql installation teaching, very detailed
chroot命令
线性表的基本概念
ipv4和ipv6对比(IPV4)
科学论文和学术论文写作
A Week of Wonderful Content Sharing (Issue 14)
0x80070570文件或目录损坏且无法删除(0x80070091怎么删除)
SAP ABAP OData 服务如何支持 $filter (过滤)操作试读版
file contains vulnerabilities
三相PWM整流器预测直接功率控制
JS列表数据通过递归实现树形结构
In Excel using ODBC consumer SAP ABAP CDS view
使用 Excel 读取 SAP ABAP CDS View 通过 ODBC 暴露出来的数据
学习爬虫之Scrapy框架学习(1)---Scrapy框架初学习及豆瓣top250电影信息获取的实战!
Caused by: 类找不到: org.apache.flink.table.planner.delegation.ParserFactory或者ExecutorFactory
初识QEMU