当前位置:网站首页>CodeTon Round 2 D. Magical Array
CodeTon Round 2 D. Magical Array
2022-08-02 02:01:00 【HeartFireY】
题目分析
给定 n n narrays with the same initial value,共有两种操作:
- 操作 1 1 1:选择一对 ( i , j ) (i, j) (i,j), a [ i − 1 ] a[i - 1] a[i−1]加 1 1 1, a [ i ] a[i] a[i]减去 1 1 1, a [ j ] a[j] a[j]减去 1 1 1, a [ j + 1 ] a[j + 1] a[j+1]加 1 1 1.
- 操作 2 2 2:选择一对 ( i , j ) (i, j) (i,j), a [ i − 1 ] a[i - 1] a[i−1]加 1 1 1, a [ i ] a[i] a[i]减去 1 1 1, a [ j ] a[j] a[j]减去 1 1 1, a [ j + 2 ] a[j + 2] a[j+2]加 1 1 1.
Only one array is executed several times 2 2 2操作,Ask which array the operation was performed on 2 2 2,操作了多少次
令 s [ ] s[] s[]表示数组 a [ ] a[] a[]的前缀和,We analyze the two operations on the prefix sum:
操作 1 1 1:Strip unaffected intervals: [ 1 , i − 2 ] , [ i + 1 , j − 1 ] , [ j + 2 , n ] [1, i - 2],[i+ 1, j - 1], [j + 2, n] [1,i−2],[i+1,j−1],[j+2,n],We denote array sums as prefix-segmented sums:
s [ i − 2 ] + ( s [ j − 1 ] − s [ i ] ) + ( s [ n ] − s [ j + 1 ] ) + a [ i − 1 ] + a [ i ] + a [ j ] + a [ j + 1 ] s[i - 2] + (s[j - 1] - s[i]) + (s[n] - s[j + 1]) + a[i - 1] + a[i] + a[j] + a[j + 1] s[i−2]+(s[j−1]−s[i])+(s[n]−s[j+1])+a[i−1]+a[i]+a[j]+a[j+1]
经过 1 1 1次操作后:Because the affected elements are continuous,So prefixes and elements are subject to − 1 -1 −1Immediately after impact + 1 +1 +1影响,不变
s [ i − 2 ] + ( s [ j − 1 ] − s [ i ] ) + ( s [ n ] − s [ j + 1 ] ) + ( a [ i − 1 ] + 1 ) + ( a [ i ] − 1 ) + ( a [ j ] − 1 ) + ( a [ j + 1 ] + 1 ) s[i - 2] + (s[j - 1] - s[i]) + (s[n] - s[j + 1]) + (a[i - 1] + 1) + (a[i] - 1) + (a[j] - 1) + (a[j + 1] + 1) s[i−2]+(s[j−1]−s[i])+(s[n]−s[j+1])+(a[i−1]+1)+(a[i]−1)+(a[j]−1)+(a[j+1]+1)
Found that prefixes and array sums are not affected操作 2 2 2:同上,Write the summation first:
s [ i − 2 ] + ( s [ j − 1 ] − s [ i ] ) + ( s [ n ] − s [ j + 2 ] ) + ( s [ j + 1 ] − s [ j ] ) + a [ i − 1 ] + a [ i ] + a [ j ] + a [ j + 2 ] s[i - 2] + (s[j - 1] - s[i]) + (s[n] - s[j + 2]) + (s[j + 1] - s[j]) + a[i - 1] + a[i] + a[j] + a[j + 2] s[i−2]+(s[j−1]−s[i])+(s[n]−s[j+2])+(s[j+1]−s[j])+a[i−1]+a[i]+a[j]+a[j+2]
经过 1 1 1次操作后,We start by analyzing the elements that are affected: a [ i − 1 ] , a [ i ] , a [ j ] , a [ j + 2 ] a[i - 1], a[i], a[j], a[j + 2] a[i−1],a[i],a[j],a[j+2],But found discontinuities due to affected elements,因此 s [ j + 1 ] , s [ j + 2 ] s[j + 1], s[j + 2] s[j+1],s[j+2]会受影响,But the impact is there a [ j + 2 ] a[j + 2] a[j+2]offset,也就是 s [ j + 2 ] s[j + 2] s[j+2]上的 − 1 -1 −1Effects are eliminated.那么:
s [ i − 2 ] + ( s [ j − 1 ] − s [ i ] ) + ( s [ n ] − s [ j + 2 ] ) + ( ( s [ j + 1 ] − 1 ) − s [ j ] ) + ( a [ i − 1 ] + 1 ) + ( a [ i ] − 1 ) + ( a [ j ] − 1 ) + ( a [ j + 1 ] + 1 ) s[i - 2] + (s[j - 1] - s[i]) + (s[n] - s[j + 2]) + ((s[j + 1] - 1) - s[j]) + (a[i - 1] + 1) + (a[i] - 1) + (a[j] - 1) + (a[j + 1] + 1) s[i−2]+(s[j−1]−s[i])+(s[n]−s[j+2])+((s[j+1]−1)−s[j])+(a[i−1]+1)+(a[i]−1)+(a[j]−1)+(a[j+1]+1)
Found prefix and array sum to be − 1 -1 −1.操作 2 2 2effect on the total,We can analyze it from the point of view of formula:
∑ i = 1 n ∑ j = 1 i a [ j ] \sum^{n}_{i = 1}\sum^{i}_{j = 1} a[j] i=1∑nj=1∑ia[j]
对 a [ x ] a[x] a[x]元素 + 1 +1 +1, a [ x + 1 ] − 1 a[x + 1] - 1 a[x+1]−1
∑ i = 1 x − 1 ∑ j = 1 i a [ j ] + ∑ i = x x ∑ j = 1 i a [ j ] + ∑ i = x n 1 + ∑ i = x + 1 n ∑ j = 1 i a [ j ] − ∑ i = x + 1 n 1 = ( ∑ i = 1 n ∑ j = 1 i a [ j ] ) + 1 \sum_{i = 1}^{x - 1}\sum_{j = 1}^{i}a[j] + \sum_{i = x}^{x}\sum_{j = 1}^{i}a[j] + \sum_{i = x}^{n}1 + \sum_{i = x + 1}^{n}\sum_{j = 1}^{i}a[j] - \sum_{i = x + 1}^{n}1 = (\sum^{n}_{i = 1}\sum^{i}_{j = 1} a[j]) + 1 i=1∑x−1j=1∑ia[j]+i=x∑xj=1∑ia[j]+i=x∑n1+i=x+1∑nj=1∑ia[j]−i=x+1∑n1=(i=1∑nj=1∑ia[j])+1
再分析 a [ y ] − 1 a[y]-1 a[y]−1, a [ x + 2 ] a[x + 2] a[x+2]元素 + 1 +1 +1:
∑ i = 1 x − 1 ∑ j = 1 i a [ j ] + ∑ i = x x ∑ j = 1 i a [ j ] − ∑ i = x n 1 + ∑ i = x + 1 n ∑ j = 1 i a [ j ] + ∑ i = x + 2 n 1 = ( ∑ i = 1 n ∑ j = 1 i a [ j ] ) − 2 \sum_{i = 1}^{x - 1}\sum_{j = 1}^{i}a[j] + \sum_{i = x}^{x}\sum_{j = 1}^{i}a[j] - \sum_{i = x}^{n}1 + \sum_{i = x + 1}^{n}\sum_{j = 1}^{i}a[j] + \sum_{i = x + 2}^{n}1 = (\sum^{n}_{i = 1}\sum^{i}_{j = 1} a[j]) - 2 i=1∑x−1j=1∑ia[j]+i=x∑xj=1∑ia[j]−i=x∑n1+i=x+1∑nj=1∑ia[j]+i=x+2∑n1=(i=1∑nj=1∑ia[j])−2
The impact was found to be: − 1 -1 −1.Then according to the above conclusion,The affected arrays and the number of operations can be found.同理,Action-Affect is 0 0 0.
Code
#include <bits/stdc++.h> #pragma gcc optimize("O2") #pragma g++ optimize("O2") #define int long long #define endl '\n' using namespace std; const int N = 1e6 + 10; int flag[N]; inline void solve(){ int n, m; cin >> n >> m; memset(flag, 0, (n + 5) * sizeof(int)); int **a = (int **)malloc((n + 2) * sizeof(int**)); int i, j; for (i = 0; i <= n; i++) { a[i] = (int*)malloc((m + 2) * sizeof(int)); } for(int i = 1; i <= n; i++){ for(int j = 1; j <= m; j++) cin >> a[i][j]; } for(int i = 1; i < m; i++){ int minn = *min_element(a[j] + 1, a[j] + 1 + n); for(int j = 1; j <= n; j++){ flag[j] += (a[j][i] -= minn); a[j][i + 1] += a[j][i]; } } int pos = 1; for(int i = 2; i <= n; i++) if(flag[pos] > flag[i]) pos = i; if(pos == 1) cout << pos << ' ' << flag[2] - flag[1] << endl; else cout << pos << ' ' << flag[1] - flag[pos] << endl; } signed main(){ ios_base::sync_with_stdio(false), cin.tie(0); int t = 1; cin >> t; while(t--) solve(); return 0; }
边栏推荐
猜你喜欢

typescript34-class的基本使用
Navicat data shows incomplete resolution

使用百度EasyDL实现厂区工人抽烟行为识别

手写博客平台~第二天

After graduating from three books, I was rejected by Tencent 14 times, and finally successfully joined Alibaba

Hiring a WordPress Developer: 4 Practical Ways

LeetCode brush diary: LCP 03. Machine's adventure

Fly propeller power space future PIE - Engine Engine build earth science

Basic use of typescript34-class
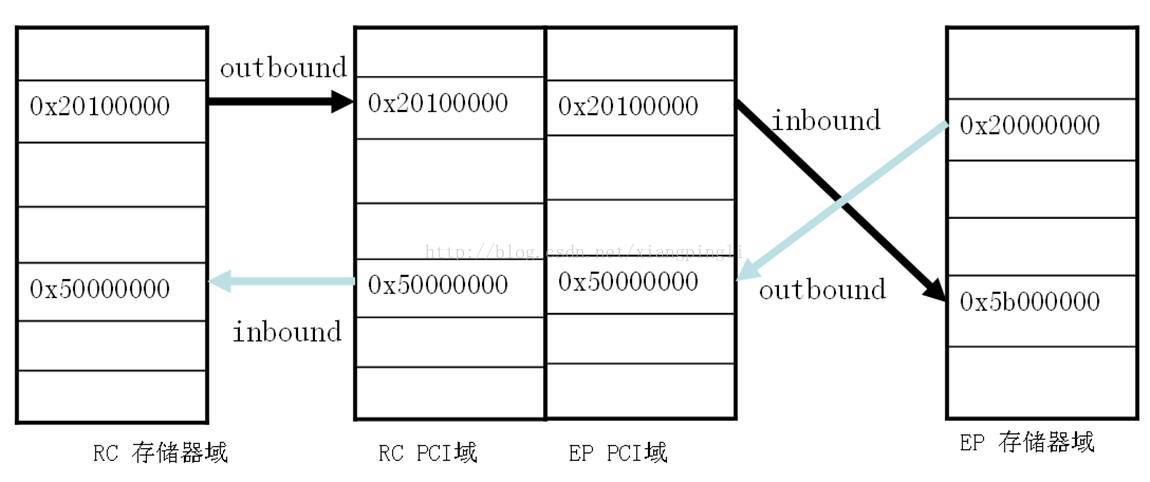
pcie inbound和outbound关系
随机推荐
AOF重写
typescript34-class的基本使用
PHP 使用 PHPRedis 与 Predis
垃圾回收器CMS和G1
牛顿定理和相关推论
Day116. Shangyitong: Details of appointment registration ※
秒懂大模型 | 3步搞定AI写摘要
"NetEase Internship" Weekly Diary (2)
3. Bean scope and life cycle
Typescript31 - any type
Kubernetes之本地存储
力扣(LeetCode)213. 打家劫舍 II(2022.08.01)
雇用WordPress开发人员:4个实用的方法
飞桨助力航天宏图PIE-Engine地球科学引擎构建
YGG 公会发展计划第 1 季总结
ofstream,ifstream,fstream读写文件
typeof in typescript32-ts
Chengdu openGauss user group recruit!
6-24 exploit-vnc password cracking
Redis Persistence - RDB and AOF