当前位置:网站首页>CodeTon Round 2 D. Magical Array 规律
CodeTon Round 2 D. Magical Array 规律
2022-08-02 01:50:00 【HeartFireY】
题目分析
给定 n n n个初始值相同的数组,共有两种操作:
- 操作 1 1 1:选择一对 ( i , j ) (i, j) (i,j), a [ i − 1 ] a[i - 1] a[i−1]加 1 1 1, a [ i ] a[i] a[i]减去 1 1 1, a [ j ] a[j] a[j]减去 1 1 1, a [ j + 1 ] a[j + 1] a[j+1]加 1 1 1。
- 操作 2 2 2:选择一对 ( i , j ) (i, j) (i,j), a [ i − 1 ] a[i - 1] a[i−1]加 1 1 1, a [ i ] a[i] a[i]减去 1 1 1, a [ j ] a[j] a[j]减去 1 1 1, a [ j + 2 ] a[j + 2] a[j+2]加 1 1 1。
只有一个数组被执行了若干次 2 2 2操作,问哪个数组被执行了操作 2 2 2,操作了多少次
令 s [ ] s[] s[]表示数组 a [ ] a[] a[]的前缀和,我们对两个操作在前缀和上进行分析:
操作 1 1 1:剥离未收到影响的区间: [ 1 , i − 2 ] , [ i + 1 , j − 1 ] , [ j + 2 , n ] [1, i - 2],[i+ 1, j - 1], [j + 2, n] [1,i−2],[i+1,j−1],[j+2,n],我们将数组和表示为前缀分段和加和式:
s [ i − 2 ] + ( s [ j − 1 ] − s [ i ] ) + ( s [ n ] − s [ j + 1 ] ) + a [ i − 1 ] + a [ i ] + a [ j ] + a [ j + 1 ] s[i - 2] + (s[j - 1] - s[i]) + (s[n] - s[j + 1]) + a[i - 1] + a[i] + a[j] + a[j + 1] s[i−2]+(s[j−1]−s[i])+(s[n]−s[j+1])+a[i−1]+a[i]+a[j]+a[j+1]
经过 1 1 1次操作后:因为受影响元素连续,因此前缀和元素受到 − 1 -1 −1影响后立即受到 + 1 +1 +1影响,不变
s [ i − 2 ] + ( s [ j − 1 ] − s [ i ] ) + ( s [ n ] − s [ j + 1 ] ) + ( a [ i − 1 ] + 1 ) + ( a [ i ] − 1 ) + ( a [ j ] − 1 ) + ( a [ j + 1 ] + 1 ) s[i - 2] + (s[j - 1] - s[i]) + (s[n] - s[j + 1]) + (a[i - 1] + 1) + (a[i] - 1) + (a[j] - 1) + (a[j + 1] + 1) s[i−2]+(s[j−1]−s[i])+(s[n]−s[j+1])+(a[i−1]+1)+(a[i]−1)+(a[j]−1)+(a[j+1]+1)
发现前缀和数组总和不受影响操作 2 2 2:同上,先写出加和式:
s [ i − 2 ] + ( s [ j − 1 ] − s [ i ] ) + ( s [ n ] − s [ j + 2 ] ) + ( s [ j + 1 ] − s [ j ] ) + a [ i − 1 ] + a [ i ] + a [ j ] + a [ j + 2 ] s[i - 2] + (s[j - 1] - s[i]) + (s[n] - s[j + 2]) + (s[j + 1] - s[j]) + a[i - 1] + a[i] + a[j] + a[j + 2] s[i−2]+(s[j−1]−s[i])+(s[n]−s[j+2])+(s[j+1]−s[j])+a[i−1]+a[i]+a[j]+a[j+2]
经过 1 1 1次操作后,我们先分析收到影响的元素: a [ i − 1 ] , a [ i ] , a [ j ] , a [ j + 2 ] a[i - 1], a[i], a[j], a[j + 2] a[i−1],a[i],a[j],a[j+2],但发现由于受影响的元素不连续,因此 s [ j + 1 ] , s [ j + 2 ] s[j + 1], s[j + 2] s[j+1],s[j+2]会受影响,但收到的影响在 a [ j + 2 ] a[j + 2] a[j+2]处抵消,也就是 s [ j + 2 ] s[j + 2] s[j+2]上的 − 1 -1 −1影响被消除。那么:
s [ i − 2 ] + ( s [ j − 1 ] − s [ i ] ) + ( s [ n ] − s [ j + 2 ] ) + ( ( s [ j + 1 ] − 1 ) − s [ j ] ) + ( a [ i − 1 ] + 1 ) + ( a [ i ] − 1 ) + ( a [ j ] − 1 ) + ( a [ j + 1 ] + 1 ) s[i - 2] + (s[j - 1] - s[i]) + (s[n] - s[j + 2]) + ((s[j + 1] - 1) - s[j]) + (a[i - 1] + 1) + (a[i] - 1) + (a[j] - 1) + (a[j + 1] + 1) s[i−2]+(s[j−1]−s[i])+(s[n]−s[j+2])+((s[j+1]−1)−s[j])+(a[i−1]+1)+(a[i]−1)+(a[j]−1)+(a[j+1]+1)
发现前缀和数组总和被 − 1 -1 −1。操作 2 2 2对总和的影响,我们可以从式子的角度分析:
∑ i = 1 n ∑ j = 1 i a [ j ] \sum^{n}_{i = 1}\sum^{i}_{j = 1} a[j] i=1∑nj=1∑ia[j]
对 a [ x ] a[x] a[x]元素 + 1 +1 +1, a [ x + 1 ] − 1 a[x + 1] - 1 a[x+1]−1
∑ i = 1 x − 1 ∑ j = 1 i a [ j ] + ∑ i = x x ∑ j = 1 i a [ j ] + ∑ i = x n 1 + ∑ i = x + 1 n ∑ j = 1 i a [ j ] − ∑ i = x + 1 n 1 = ( ∑ i = 1 n ∑ j = 1 i a [ j ] ) + 1 \sum_{i = 1}^{x - 1}\sum_{j = 1}^{i}a[j] + \sum_{i = x}^{x}\sum_{j = 1}^{i}a[j] + \sum_{i = x}^{n}1 + \sum_{i = x + 1}^{n}\sum_{j = 1}^{i}a[j] - \sum_{i = x + 1}^{n}1 = (\sum^{n}_{i = 1}\sum^{i}_{j = 1} a[j]) + 1 i=1∑x−1j=1∑ia[j]+i=x∑xj=1∑ia[j]+i=x∑n1+i=x+1∑nj=1∑ia[j]−i=x+1∑n1=(i=1∑nj=1∑ia[j])+1
再分析 a [ y ] − 1 a[y]-1 a[y]−1, a [ x + 2 ] a[x + 2] a[x+2]元素 + 1 +1 +1:
∑ i = 1 x − 1 ∑ j = 1 i a [ j ] + ∑ i = x x ∑ j = 1 i a [ j ] − ∑ i = x n 1 + ∑ i = x + 1 n ∑ j = 1 i a [ j ] + ∑ i = x + 2 n 1 = ( ∑ i = 1 n ∑ j = 1 i a [ j ] ) − 2 \sum_{i = 1}^{x - 1}\sum_{j = 1}^{i}a[j] + \sum_{i = x}^{x}\sum_{j = 1}^{i}a[j] - \sum_{i = x}^{n}1 + \sum_{i = x + 1}^{n}\sum_{j = 1}^{i}a[j] + \sum_{i = x + 2}^{n}1 = (\sum^{n}_{i = 1}\sum^{i}_{j = 1} a[j]) - 2 i=1∑x−1j=1∑ia[j]+i=x∑xj=1∑ia[j]−i=x∑n1+i=x+1∑nj=1∑ia[j]+i=x+2∑n1=(i=1∑nj=1∑ia[j])−2
发现影响为: − 1 -1 −1。那么根据以上结论,可以找出被影响的数组及操作次数。同理,操作一影响为 0 0 0。
Code
#include <bits/stdc++.h> #pragma gcc optimize("O2") #pragma g++ optimize("O2") #define int long long #define endl '\n' using namespace std; const int N = 1e6 + 10; int flag[N]; inline void solve(){ int n, m; cin >> n >> m; memset(flag, 0, (n + 5) * sizeof(int)); int **a = (int **)malloc((n + 2) * sizeof(int**)); int i, j; for (i = 0; i <= n; i++) { a[i] = (int*)malloc((m + 2) * sizeof(int)); } for(int i = 1; i <= n; i++){ for(int j = 1; j <= m; j++) cin >> a[i][j]; } for(int i = 1; i < m; i++){ int minn = *min_element(a[j] + 1, a[j] + 1 + n); for(int j = 1; j <= n; j++){ flag[j] += (a[j][i] -= minn); a[j][i + 1] += a[j][i]; } } int pos = 1; for(int i = 2; i <= n; i++) if(flag[pos] > flag[i]) pos = i; if(pos == 1) cout << pos << ' ' << flag[2] - flag[1] << endl; else cout << pos << ' ' << flag[1] - flag[pos] << endl; } signed main(){ ios_base::sync_with_stdio(false), cin.tie(0); int t = 1; cin >> t; while(t--) solve(); return 0; }
边栏推荐
- Kubernetes — Flannel
- Two ways to pass feign exceptions: fallbackfactory and global processing Get server-side custom exceptions
- Effects of Scraping and Aggregation
- 6-25 Vulnerability Exploitation - irc Backdoor Exploitation
- R语言使用table1包绘制(生成)三线表、使用单变量分列构建三线表、编写自定义三线表结构(将因子变量细粒度化重新构建三线图)、自定义修改描述性统计参数输出自定义统计量
- LeetCode刷题日记:LCP 03.机器人大冒险
- 3. Bean scope and life cycle
- typescript38-class的构造函数实例方法继承(implement)
- pcie inbound和outbound关系
- Rust P2P网络应用实战-1 P2P网络核心概念及Ping程序
猜你喜欢

【Brush the title】Family robbery

大话西游创建角色失败解决
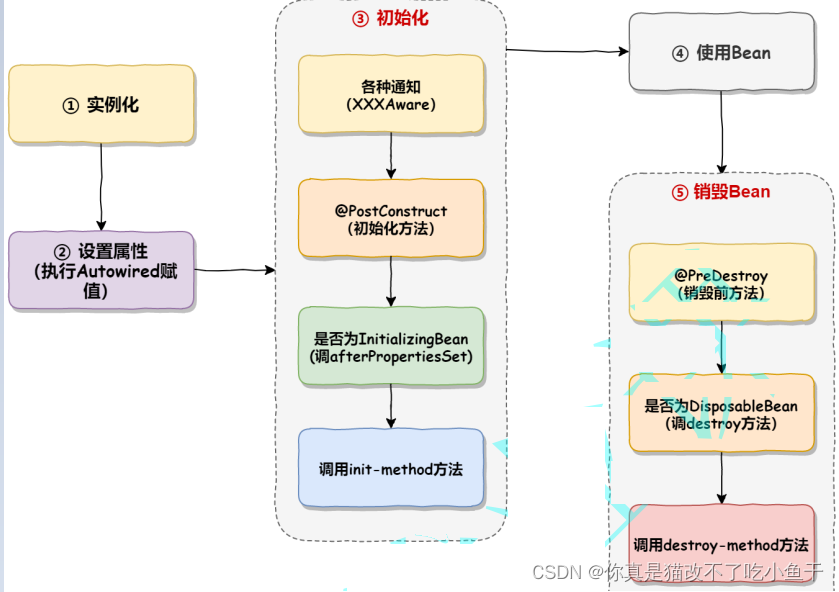
3. Bean scope and life cycle

一本适合职场新人的好书
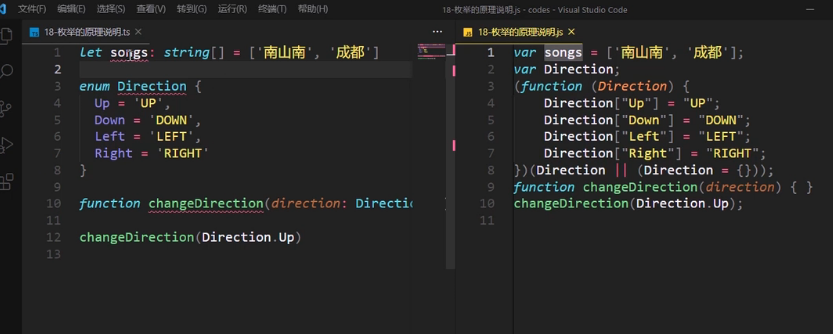
The characteristics and principle of typescript29 - enumeration type
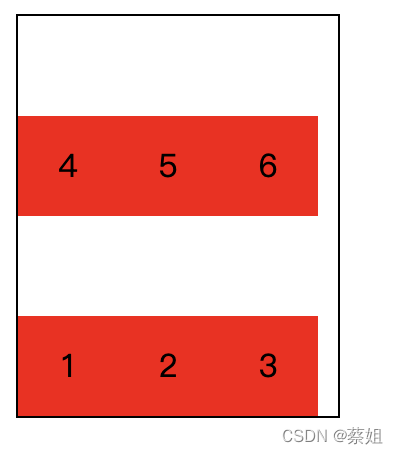
Use flex-wrap to wrap lines in flex layout

Local storage in Kubernetes

Day116.尚医通:预约挂号详情 ※
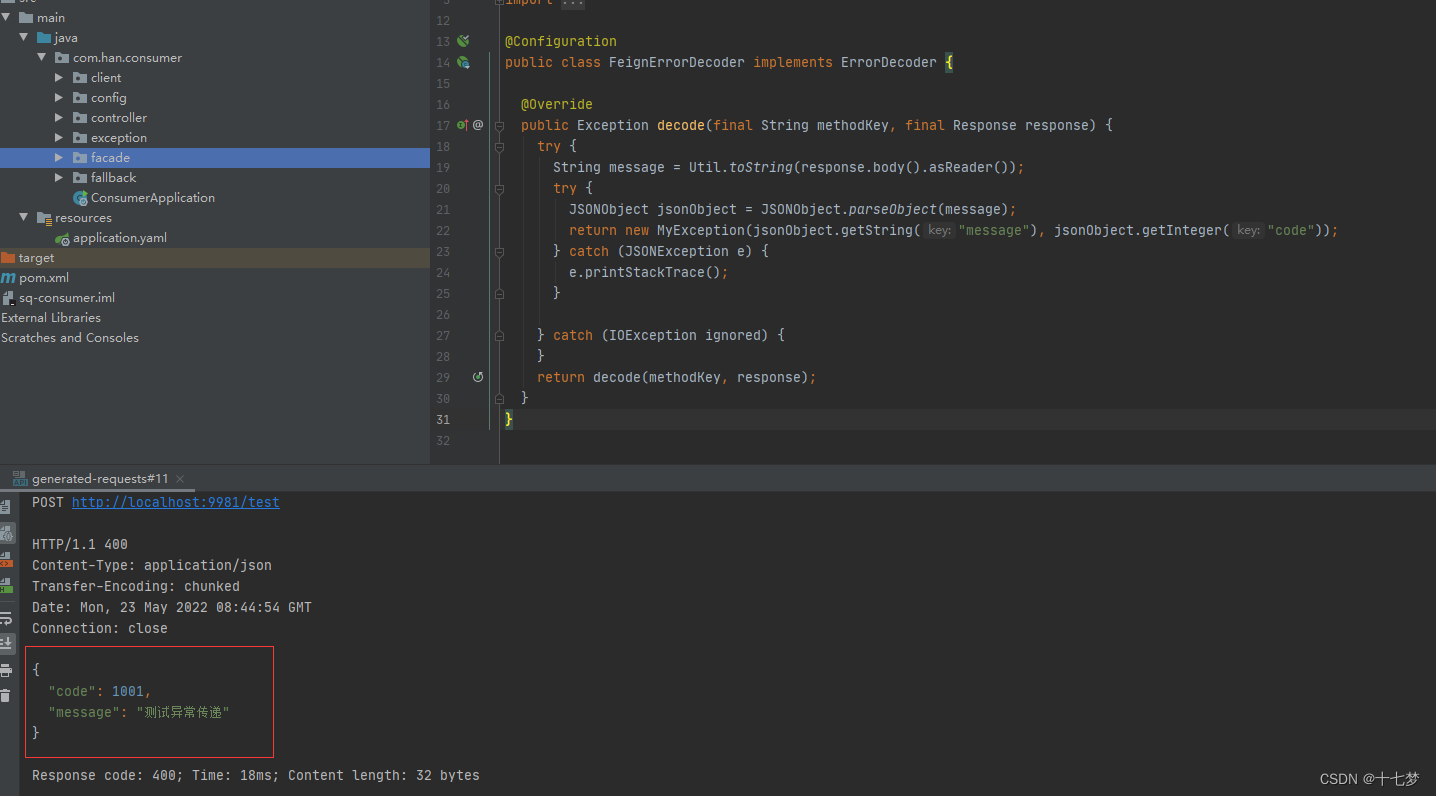
Two ways to pass feign exceptions: fallbackfactory and global processing Get server-side custom exceptions

Rust P2P网络应用实战-1 P2P网络核心概念及Ping程序
随机推荐
Two ways to pass feign exceptions: fallbackfactory and global processing Get server-side custom exceptions
Rust P2P Network Application Combat-1 P2P Network Core Concepts and Ping Program
手写一个博客平台~第一天
YGG 公会发展计划第 1 季总结
Anti-oversold and high concurrent deduction scheme for e-commerce inventory system
Day116. Shangyitong: Details of appointment registration ※
云和恩墨:让商业数据库时代的价值在openGauss生态上持续繁荣
Navicat data shows incomplete resolution
有效进行自动化测试,这几个软件测试工具一定要收藏好!!!
Win Go开发包安装配置、GoLand配置
HSDC is related to Independent Spanning Tree
PHP直播源码实现简单弹幕效果的相关代码
力扣、752-打开转盘锁
typescript33-typescript高级概述
飞桨助力航天宏图PIE-Engine地球科学引擎构建
typescript35-class的构造函数
Kubernetes — Flannel
When paying attention to the "Internet +" model, you usually only focus on the "Internet +" model itself
MySQL——增删查改操作
LeetCode Review Diary: 34. Find the first and last position of an element in a sorted array