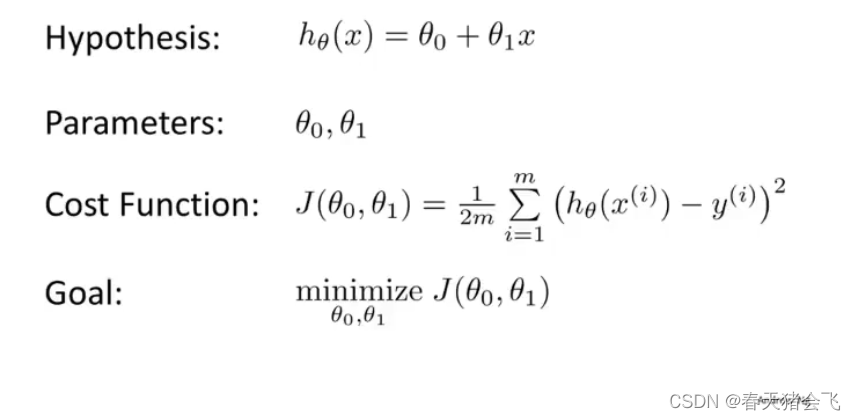每日一题-二分法

目录

搜索旋转排序数组

在排序数组中查找元素的第一个和最后一个位置

---

搜索旋转排序数组

• 2022.07.25
• 题目

整数数组 nums 按升序排列，数组中的值 互不相同 。在传递给函数之前，nums 在预先未知的某个下标 k（0 <= k < nums.length）上进行了 旋转，使数组变为 [nums[k], nums[k+1], ..., nums[n-1], nums[0], nums[1], ..., nums[k-1]]（下标 从 0 开始 计数）。例如， [0,1,2,4,5,6,7] 在下标 3 处境旋转后可能变为 [4,5,6,7,0,1,2] 。给你 旋转后 的数组 nums 和一个整数 target ，如果 nums 中存在这个目标值 target ，则返回它的下标，否则返回 -1 。

你必须设计一个时间复杂度为 O(log n) 的算法解决此问题。

• 思路
  • 通过要求的时间复杂度倒推，即二分法。二分法的前提是什么？当然是要求数组是排好顺序的
  • 数组是从某个位置旋转的，如果说当前的中间位置的数字比最左面的数字大，证明左半侧是单调递增的；如果小于，证明后面是单调递增的
  • 从这个角度进行切入
  • 还有一个容易忽略的点就是，当数组只有或者只剩下两个数字时，需要考虑nums[mid]是否等于nums[left]，因为这个时候边界就是目标值了：比如10
• 代码

public int search(int[] nums, int target) {
        //logn的复杂度 二分法
        if(nums == null || nums.length <= 0)
            return -1;
        if(target == nums[0])
            return 0;
        if(nums[nums.length - 1] == target)
            return nums.length - 1;
        int left = 0, right = nums.length - 1;
        while(left <= right){
            int mid = left + (right - left) / 2;
            if(target == nums[mid])
                return mid;
            else if(nums[mid] >= nums[left]){//证明左面是递增的 这里用等号的原因是当只有两个数字的时候，比如10，如果不用等号，1或者0就会找不到
                if(target >= nums[left] && target < nums[mid]){
                    right = mid - 1;
                }else{
                    left = mid + 1;
                }
            }else{
                if(target > nums[mid] && target <= nums[right]){
                    left = mid + 1;
                }else{
                    right = mid - 1;
                }
            }
        }
        return -1;
    }

在排序数组中查找元素的第一个和最后一个位置

• 2022.07.26
• 题目

给你一个按照非递减顺序排列的整数数组 nums，和一个目标值 target。请你找出给定目标值在数组中的开始位置和结束位置。如果数组中不存在目标值 target，返回 [-1, -1]。你必须设计并实现时间复杂度为 O(log n) 的算法解决此问题。

• 思路
  • 算法复杂度要求是log(n)，依然是二分法
  • 找到target的第一个下标和最后一个下标，当匹配到nums[mid]==target的时候，依次向前和向后找，直到对应的值不等于target
• 代码

public int[] searchRange(int[] nums, int target) {
        if(nums == null || nums.length <= 0)
            return new int[]{-1, -1};
        if(target > nums[nums.length - 1])
            return new int[]{-1, -1};
        if(target < nums[0])
            return new int[]{-1, -1};
        int left = 0, right = nums.length - 1;
        while(left <= right){
            int mid = left + (right - left) / 2;
            if(nums[mid] == target){
                int index1 = mid, index2 = mid;
                while((-- index1 >= 0) && nums[index1] == target);
                while((++ index2 <= nums.length - 1) && nums[index2] == target);
                // 这里是因为先执行的加和减，在结果的时候要加回去，否则会小一个以及大一个
                return new int[]{index1 + 1, index2 - 1};
            }else if(nums[mid] < target){
                left = mid + 1;
            }else{
                right = mid - 1;
            }
        }
        return new int[]{-1, -1};
    }