当前位置:网站首页>第二章:4位卡普雷卡数,搜索偶数位卡普雷卡数,搜索n位2段和平方数,m位不含0的巧妙平方数,指定数字组成没有重复数字的7位平方数,求指定区间内的勾股数组,求指定区间内的倒立勾股数组
第二章:4位卡普雷卡数,搜索偶数位卡普雷卡数,搜索n位2段和平方数,m位不含0的巧妙平方数,指定数字组成没有重复数字的7位平方数,求指定区间内的勾股数组,求指定区间内的倒立勾股数组
2022-07-03 19:18:00 【股_四】
//4位卡普雷卡数
int main()
{
int a, b, c, x, y;
printf(" 4位卡普雷卡数有:");
c = (int)sqrt(1000);
for (b = c + 1; b <= 99; b++) // 枚举2位数b
{
a = b * b;
x = a / 100; // a 分为前后两个2公
y = a % 100; // 分段和条件检验
if( y >= 10 && b == (x + y))
printf("%d, ", a);
}
return 0;
}
结果: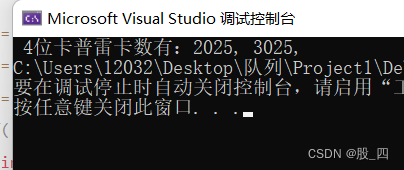
//搜索偶数位卡普雷卡数
int main()
{
double a, b, m, w, x, y;
int k, n; long c, d;
printf("请输入偶数n(n≤14) :");
scanf("%d", &n);
if (n % 2 > 0)
{
printf(" 请输入偶数!\n");
return 0;
}
printf(" % d位卡普雷卡数有: \n", n);
for (m = 1, k = 2;k <= n; k++)m *= 10;
for (w = 1, k = 1 ; k <= n / 2; k++)w *= 10;
c = (long)pow(m, 0.5);
d = (long)pow(10 * m - 1, 0.5); // 求出枚举上循环的起点与终点
for (b = c + 1; b <= d; b++)
{
a = b * b;
x = floor(a / w);
y = fmod(a, w);//n位平方数a分为前后数x、y
if (b == x + y && y >= w / 10) //分段和条件检验
printf(" %.0f= (%.0f+%.0f)^2 \n",a,x,y);
}
return 0;
}
结果:
//搜索n位2段和平方数
int main()
{
double a, b, m, w, x, y;
long c, d; int k, n, s = 0;
printf(" 请输入正整数n (3<n<16:");
scanf(" %d", &n);
for (m = 1, k = 2; k <= n; k++) m *= 10;
c = (long)pow(m, 0.5);
d = (long)pow(10 * m - 1, 0.5);
for (b = c + 1; b <= d; b++)
{
a = b * b;
w = 1;
for (k = 1; k <= n - 1; k++)
{
w *= 10;
x = floor(a / w);
y = fmod(a, w);
if (b == x + y && y > 0)
{
s++;
printf(" % .0f = ( % .0f + % .0f) ^ 2\n", a, x, y);
}
}
}
if (s > 0)
printf("共%d个%d 位2段和平方数 \n", s, n);
else printf("没有 % d位2段和平方数。 \n", n) ;
}
结果: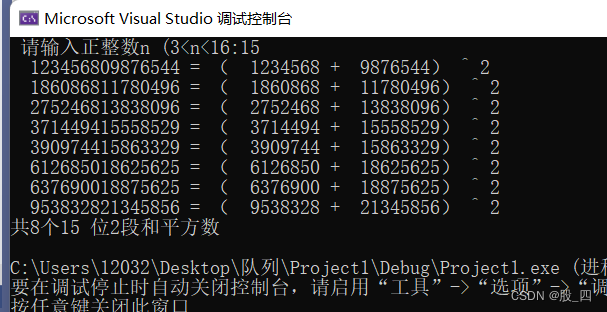
//m位不含0的巧妙平方数
int main()
{
int k, m, n, i, x, b[10];
long t, t1, t2, y, d, f;
printf(" 把 1,2,..,9这9个数字选m个, ");
printf(" 组合成没有重复数字的平方数。\n");
printf(" 请输入平方数的位数m:");
scanf("%d", &m);
n = 0;
t = 1;
for (y = 1; y <= m - 1; y++)
t = t * 10;
t1 = (long)sqrt(t);
t2 = (long)sqrt(10 * t);
for (y = t1 + 1; y <= t2; y++)
{
f = y * y;
d = f;
for (i = 1; i <= 9; i++)
b[i] = 0;
for (x = 0, i = 1; i <= m; i++)
{
k = f % 10;
f = f / 10;
if (k == 0 || (++b[k] > 1))
{
x = 1;
break;
}
}
if (x == 0)
{
n++;
printf(" %1d=%d^2", d, y);
if (n % 3 == 0) printf("\n");
}
}
printf(" \n 共%d个\n", n);
return 0;
}
结果: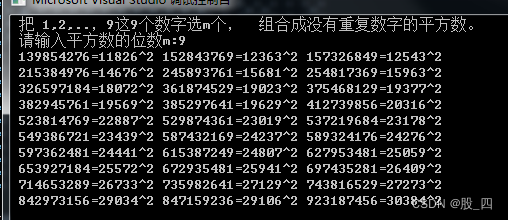
int main()
{
int k, m, n, t, f[10];
long a, b, c, d, w;
printf(" 数字2、3、5、6、7、8、9的全排列中的平方数:\n");
n = 0;
b = (long)sqrt(2356789);
c = (long)sqrt(9876532);
for (a = b; a <= c; a++)
{
d = a * a; w = d; //确保d为平方数
for (k = 0; k <= 9; k++) f[k] = 0;
while (w > 0)
{
m = w % 10;
f[m]++;
w = w / 10;
}
for (t = 0, k = 1; k <= 9; k++)
if (f[k] > 1) t = 1; //测试三个平方数是否有重复数字
if (t == 0 && f[0] + f[1] + f[4] == 0) //测试平方数中没有数字0、1、4
{
n++;
printf(" %2d:", n);
printf(" %1d=%1d 2 \n", d, a);
}
}
printf(" 共可组成以上%d个", n);
return 0;
}
结果: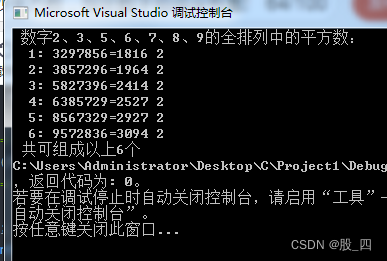
//求指定区间内的勾股数组
int main()
{
int a, b, n;
long x, y, z, d;
printf(" 请输入区间[a,6]的上下限a,b: ");
scanf("%d, %d", &a, &b);
printf(" 区间[%d,%d]中的勾股数组有:\n",a,b);
n=0;
for (x=a;x<=b-2;x++)
for (y = x + 1; y <= b - 1; y++)
{
d = x * x + y * y;
z = sqrt(d); //2为x,的平方和开平方
if (z > b) break;
if (z * z == d) //满足勾股数条件时输出
{
n++;
printf(" %ld^2+%ld^2=%1d^2 \n", x, y, z);
}
}
printf(" 共%d 组勾股数", n);
return 0;
}
结果: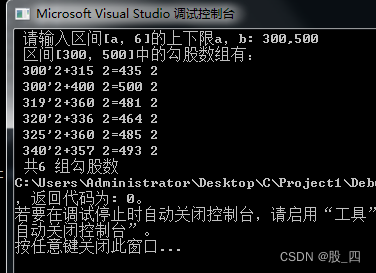
//,求指定区间内的倒立勾股数组
int main()
{
int a, b, n;
long x, y, z;
printf(" 请输入区间[a,6]的上下限a,b: ");
scanf("%d,%d", &a, &b);
printf(" 区间[%d,%d]中的勾股数组有:\n",a,b);
n=0;
for(z = a; z <= b -2; z++)
for(y = z + 1;y <=b - 1; y++)
for(x = y + 1;x <= b;x++)
if(z*z*( x * x + y * y) == x*x*y*y)
{
n++;
printf(" 1/%ld^2+1/%ld^2=1/%1d^2 \n", x, y, z);
}
printf(" 共%d 组倒立勾股数", n);
return 0;
}
结果: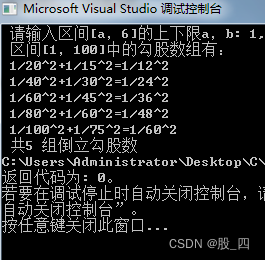
边栏推荐
- Flutter网络和数据存储框架搭建 -b1
- The way to treat feelings
- [wallpaper] (commercially available) 70 wallpaper HD free
- Record: MySQL changes the time zone
- Zhang Fei hardware 90 day learning notes - personal records on day 4, please see my personal profile / homepage for the complete
- 第二十章:y= sin(x)/x,漫步坐标系计算,y= sin(x)/x 带廓幅图形,奥运五环,小球滚动与弹跳,流水显示,矩形优化裁剪,r个皇后全控nxn棋盘
- 第一章:拓广同码小数和s(d, n)
- Failed to start component [StandardEngine[Catalina]. StandardHost[localhost]. StandardContext
- How to design a high concurrency system
- High concurrency architecture cache
猜你喜欢
第一章:求n的阶乘n!

This Chinese numpy quick look-up table is too easy!

Ctrip will implement a 3+2 work system in March, with 3 days on duty and 2 days at home every week

Smart wax therapy machine based on STM32 and smart cloud
QT -- qfile file read / write operation

The online customer service system developed by PHP is fully open source without encryption, and supports wechat customer service docking
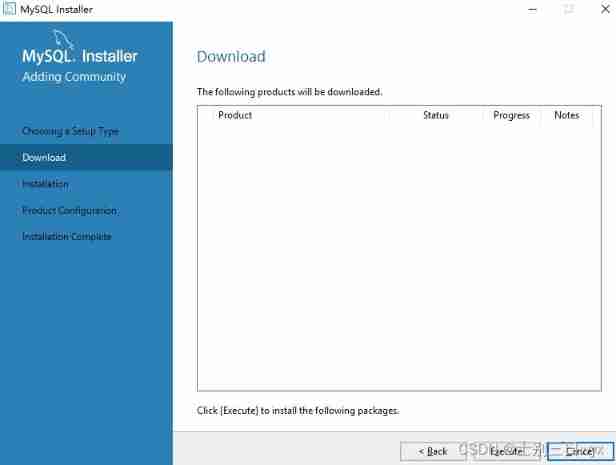
During MySQL installation, the download interface is empty, and the components to be downloaded are not displayed. MySQL installer 8.0.28.0 download interface is empty solution
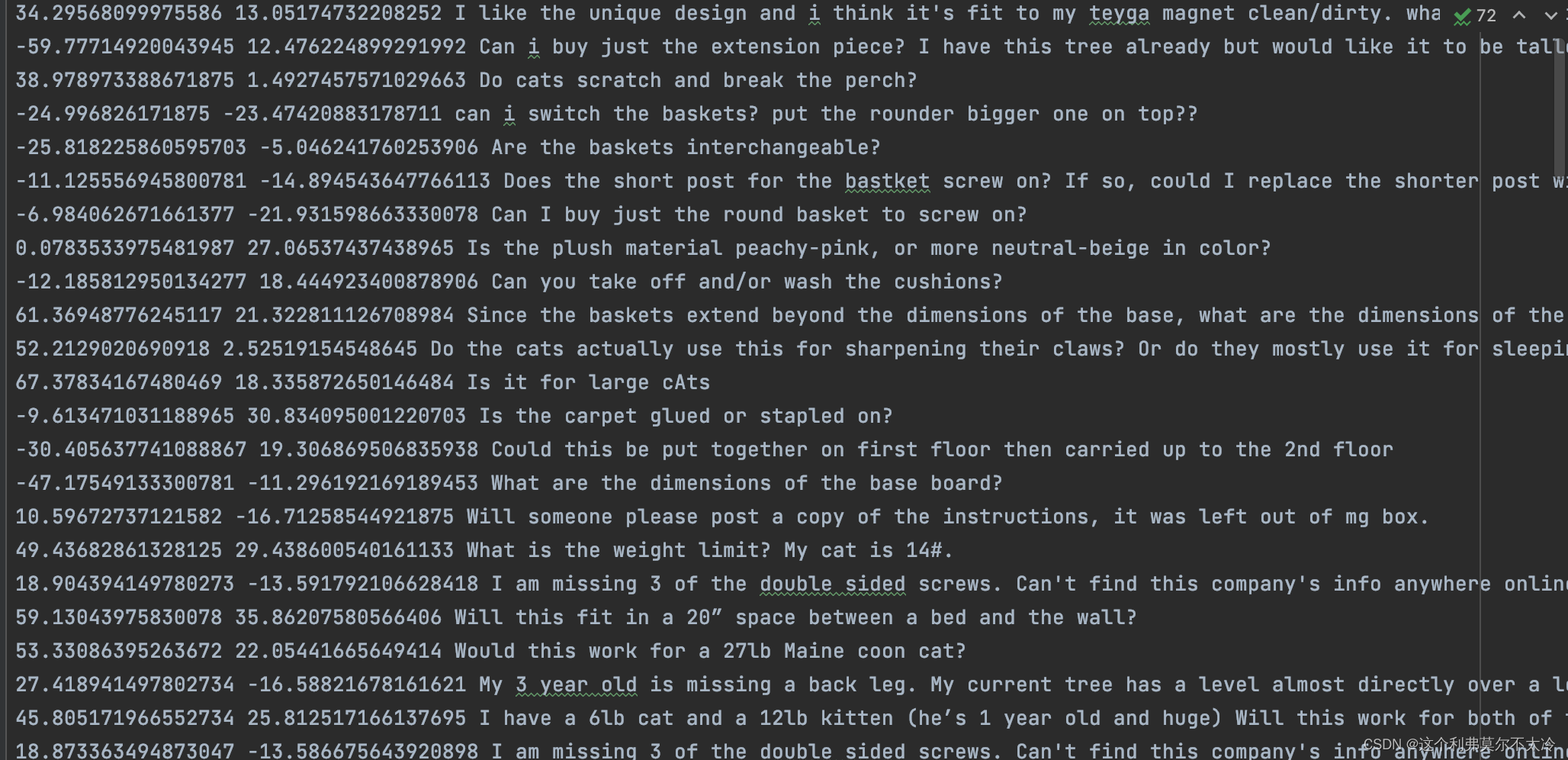
Using the visualization results, click to appear the corresponding sentence
![[academic related] how to find the innovation of top papers? Chinese universities won the CVPR Best Student Thesis Award for the first time](/img/06/5a37e2dca9711f8322b657581c3d75.png)
[academic related] how to find the innovation of top papers? Chinese universities won the CVPR Best Student Thesis Award for the first time
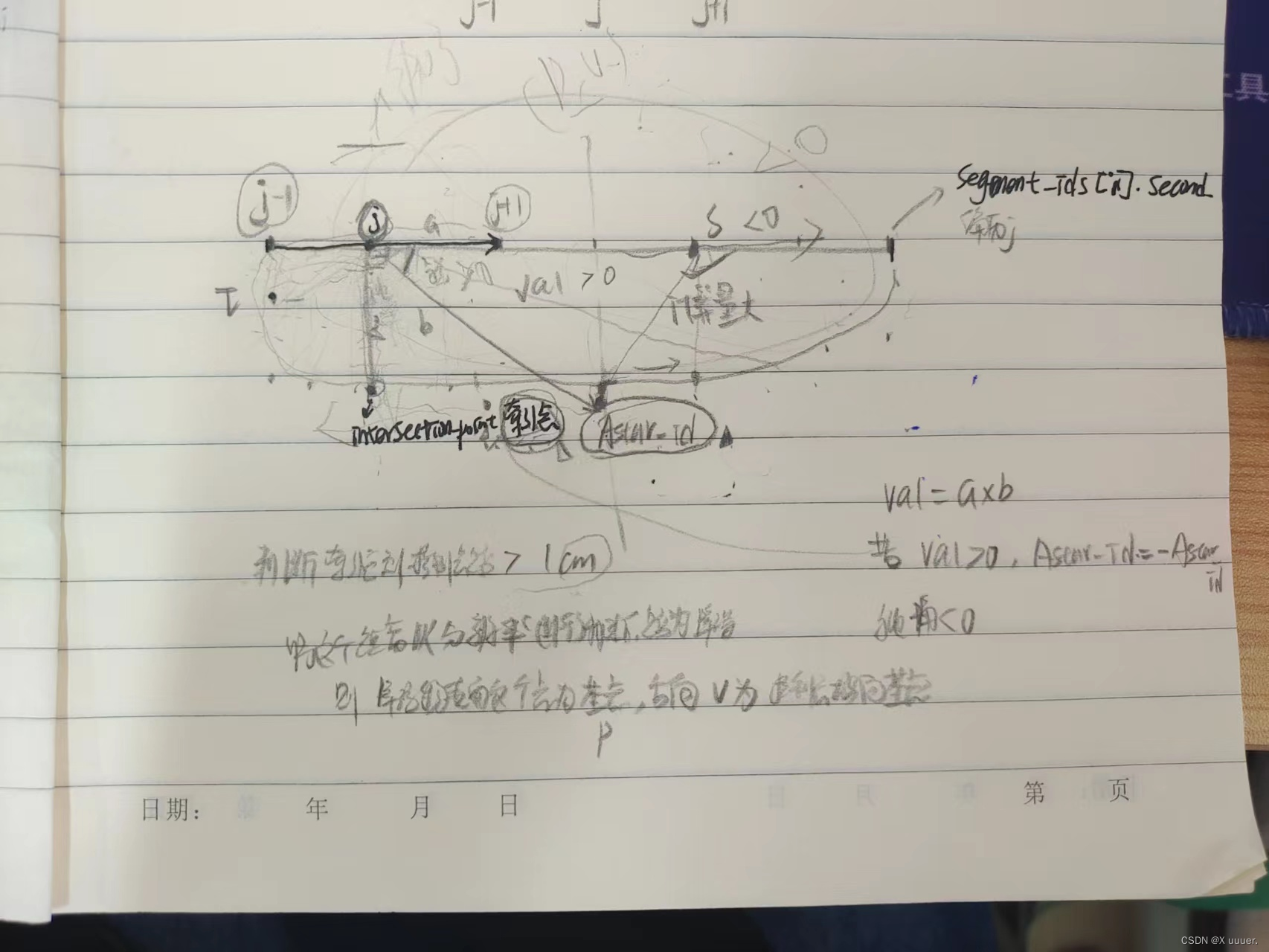
EGO Planner代码解析bspline_optimizer部分(2)
随机推荐
第一章:三位阶乘和数,图形点扫描
Random numbers in a long range, is that right- Random number in long range, is this the way?
Analyse du Code du planificateur ego bspline Section Optimizer (1)
EGO Planner代码解析bspline_optimizer部分(3)
Sentinel source code analysis part II - sentinel dashboard console startup and configuration
High concurrency Architecture - distributed search engine (ES)
Scrape crawler framework
EGO Planner代码解析bspline_optimizer部分(2)
2022.2.14 Li Kou - daily question - single element in an ordered array
[free sharing] kotalog diary2022 plan electronic manual ledger
How does if ($variable) work? [repeat] - how exactly does if ($variable) work? [duplicate]
Luogu-p1107 [bjwc2008] Lei Tao's kitten
Record: MySQL changes the time zone
[new year job hopping season] test the technical summary of interviewers' favorite questions (with video tutorials and interview questions)
第一章:拓广同码小数和s(d, n)
第一章:求所有阶乘和数,大奖赛现场统分程序设计,三位阶乘和数,图形点扫描,递归求n的阶乘n!,求n的阶乘n!,舍罕王失算
【数学建模】基于matlab船舶三自由度MMG模型【含Matlab源码 1925期】
UE source code analysis: uccharactermovementcomponent - rootmotion
If the warehouse management communication is not in place, what problems will occur?
變化是永恒的主題