当前位置:网站首页>There are n steps in total, and you can go up to 1 or 2 steps each time. How many ways are there?
There are n steps in total, and you can go up to 1 or 2 steps each time. How many ways are there?
2022-08-04 02:09:00 【Xxhu1997】
CSDN每日一练题目
- 2022-08-02日CSDNPractice one question of medium difficulty every day.
- 题目要求 1 <= N <= 50,当输入NThe result is calculated within a second.
- 题目类型:递归、循环

answering process
测试示例:
- n = 3 , 正确结果为 3
- n = 4 , 正确结果为 5
- n = 5 , 正确结果为 8
- n = 6 , 正确结果为13
1、Ordinary recursion
- The idea was not very clear at first,就随便写写,Write a recursion,但是当N较大时,计算效率极低.
代码
class Main {
public static void main(String[] args) {
System.out.println(System.currentTimeMillis());
int n = 50;
int result = solution(n);
System.out.println(result);
System.out.println(System.currentTimeMillis());
}
public static int solution(int n) {
int result = 0;
if (n >= 1 && n <= 2){
result = n;
} else {
result = solution(n -1) + solution(n - 2);
}
return result;
}
}
结果
- because of the long computation time,Officials have not stated whether the calculation results are correct,Just stating the timeout.
2、递归优化
- The first type of recursion is very inefficient,So think about optimizing recursion.
- 优化思路:Because you can only go1级或2级台阶,Then you can go first1级和2The total type of collocation,举例说明:如共5级台阶,Then you can be sure1和2There are matching methods:5次1级、3次1级和1次2级、1次1级和2次2级.Regardless of the first step1级或2级,There are three basic combinations,Determine these three combinations first,Then you can sort each combination.
代码
class Main {
public static void main(String[] args) {
System.out.println(System.currentTimeMillis());
int n = 20;
int result = solution(n);
System.out.println(result);
System.out.println(System.currentTimeMillis());
}
public static int solution(int n) {
int result = 0;
for (int oneNum = n; oneNum >= 0; oneNum--) {
if ((n - oneNum) % 2 == 0) {
result += countNum(oneNum, (n - oneNum) / 2);
}
}
return result;
}
public static int countNum(int oneNum, int twoNum) {
if (oneNum == 0 || twoNum == 0) {
return 1;
} else if (oneNum == 1 || twoNum == 1) {
return oneNum + twoNum;
}
int total = 0;
for (int i = 0; i <= oneNum; i++) {
if (oneNum - i == 0) {
total += 1;
} else {
total += countNum(oneNum - i, twoNum - 1);
}
}
return total;
}
}
结果
- Although optimization has a certain effect,但当NIt's still slow when larger,So this way of writing is not the answer.
3、Use permutation formulas、并优化
在第二种写法时,递归的时候,I already thought it was a permutation and combination problem I learned in high school,Because I can't remember what the formula is,did not practice.但结果仍然不对,Then we can only think about whether it is feasible to use the permutation and combination formula of high school.
排列公式:The permutation formula does not apply in this question
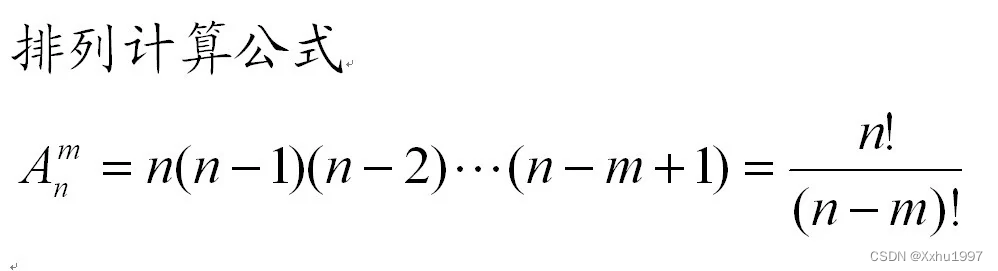
组合公式:Among them, the factorial formula is more suitable to use,Convert to this topic,公式中
n就是走1Levels and walks2The sum of the number of stages,m可以是1level or2number of stages,结果相同.
Basic permutations
class Main {
public static void main(String[] args) {
System.out.println(System.currentTimeMillis());
int n = 20;
int result = solution(n);
System.out.println(result);
System.out.println(System.currentTimeMillis());
}
public static int solution(int n) {
int result = 0;
for (int oneNum = n; oneNum >= 0; oneNum--) {
if ((n - oneNum) % 2 == 0) {
result += countNum(oneNum, (n - oneNum) / 2);
}
}
return result;
}
public static int countNum(int oneNum, int twoNum) {
if (oneNum == 0 || twoNum == 0) {
return 1;
} else if (oneNum == 1 || twoNum == 1) {
return oneNum + twoNum;
}
int total = 0;
int top = 1;
for (int i = oneNum + twoNum; i > 1; i--) {
top *= i;
}
int down = 1;
for (int i = oneNum; i > 1; i--) {
down *= i;
}
for (int i = twoNum; i > 1; i--) {
down *= i;
}
total = top / down;
return total;
}
}
结果
- Test with this code,当N过大时,The calculation cannot be performed properly,会报错,原因是当N过大时,The number after factorial is too large,Out of range for type storage number,causes the numbers to become 0,Ultimately resulting in a denominator of 0计算出错.
Optimize formula calculation logic
- 优化思路:
- 1、Reduce the formula first,Decrease the factorial value
- 2、mChoose a lower number,如果走1The number of steps is small,就将1The number of steps is set to m,反之则是2number of steps.
class Main {
public static void main(String[] args) {
System.out.println(System.currentTimeMillis());
int n = 20;
int result = solution(n);
System.out.println(result);
System.out.println(System.currentTimeMillis());
}
public static int solution(int n) {
int result = 0;
for (int oneNum = n; oneNum >= 0; oneNum--) {
if ((n - oneNum) % 2 == 0) {
result += countNum(oneNum, (n - oneNum) / 2);
}
}
return result;
}
public static int countNum(int oneNum, int twoNum) {
if (oneNum == 0 || twoNum == 0) {
return 1;
} else if (oneNum == 1 || twoNum == 1) {
return oneNum + twoNum;
}
int total = 0;
int topMin = 1;
int downMax = 1;
if (oneNum > twoNum) {
topMin = oneNum;
downMax = twoNum;
} else {
topMin = twoNum;
downMax = oneNum;
}
int top = 1;
for (int i = oneNum + twoNum; i > topMin; i--) {
top *= i;
}
int down = 1;
for (int i = downMax; i > 1; i--) {
down *= i;
}
total = top / down;
return total;
}
}
总结
- 结果:很不幸,I did not seriously recall the permutation and combination formula that day,As a result, this scheme after optimization is not written,In the end no results were submitted,Not sure if the final answer is correct.
- 感悟:
- 1、Many problems can be solved in middle school and high school,Too bad you forgot.
- 2、Don't give up on some issues,the chacha,能节省很多时间.
- 3、Algorithms are hard.-.-
边栏推荐
- 在Activity中获取另一个XML文件的控件
- html select标签赋值数据库查询结果
- Please refer to dump files (if any exist) [date].dump, [date]-jvmRun[N].dump and [date].dumpstream.
- Kubernetes:(九)coredns(浪不动了)
- 2022年T电梯修理考题及答案
- DDTL: Domain Transfer Learning at a Distance
- 共n级台阶,每次可以上1级或2级台阶,有多少种上法?
- 参加Oracle OCP和MySQL OCP考试的学员怎样在VUE预约考试
- C语言:学生管理系统(链表版)
- JS 从零教你手写节流throttle
猜你喜欢

nodejs+express realizes the access to the database mysql and displays the data on the page

Example 035: Setting the output color
HBuilderX的下载安装和创建/运行项目

MallBook 助力SKT思珂特教育集团,立足变化,拥抱敏捷交易
esp32发布机器人电池电压到ros2(micro-ros+CoCube)
云开发旅游打卡广场微信小程序源码(含视频教程)

实例035:设置输出颜色
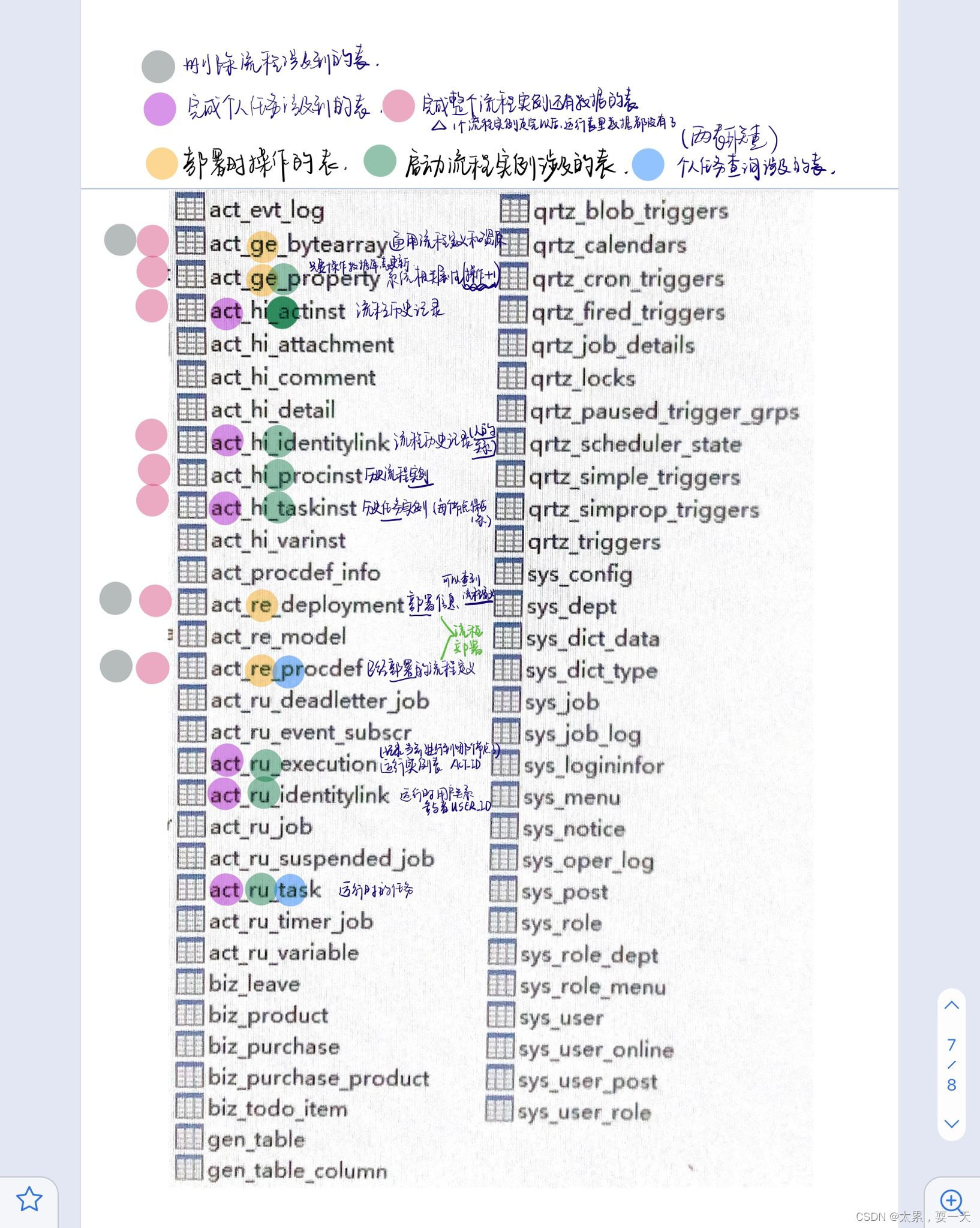
activiti流程执行过程中,数据库表的使用关系
html select tag assignment database query result
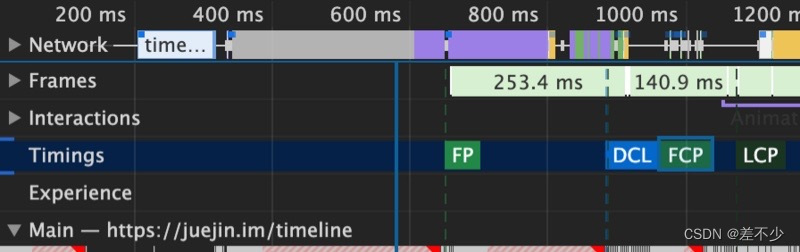
计算首屏时间
随机推荐
web端动效 lottie-web 使用
编写 BOLL 心得体会
Continuing to invest in product research and development, Dingdong Maicai wins in supply chain investment
2022焊工(初级)上岗证题目模拟考试平台操作
priority_queue元素为指针时,重载运算符失效
STM32-遥感数据处理
Intranet penetration - application
实例039:有序列表插入元素
FeatureNotFound( bs4.FeatureNotFound: Couldn't find a tree builder with the features you requested:
Priority_queue element as a pointer, the overloaded operators
瑞能微计量芯片RN2026的实用程序
Zabbix设置邮件告警+企业微信告警
html select tag assignment database query result
2022年T电梯修理考题及答案
大佬们,读取mysql300万单表要很长时间,有什么参数可以优惠,或者有什么办法可以快点
C程序编译和预定义详解
C语言力扣第54题之螺旋矩阵。模拟旋转
GNSS[0]- Topic
持续投入商品研发,叮咚买菜赢在了供应链投入上
v-model