当前位置:网站首页>Slipper - virtual point, shortest path
Slipper - virtual point, shortest path
2022-08-04 01:07:00 【Small dimples.】
题意
The given root node is 1,节点数为 n n n 的一棵树,n-1 side right w i w_i wi.
如果两个点 u , v u, v u,v The difference in depth is k ( ∣ d e p u − d e p v ∣ = k ) k\ (|dep_u−dep_v|=k) k (∣depu−depv∣=k) ,can reach each other directly,花费为 p p p.
给定起点和终点,Ask the minimum cost from start to finish.
2 ≤ n ≤ 1 0 6 , 1 ≤ u , v ≤ n , 1 ≤ w ≤ 1 0 6 . 2≤n≤10^6,\ 1≤u,v≤n,\ 1≤w≤10^6. 2≤n≤106, 1≤u,v≤n, 1≤w≤106.
1 ≤ k ≤ m a x u ⊆ V ( d e p u ) , 0 ≤ p ≤ 1 0 6 . 1≤k≤max_u⊆V(dep_u),\ 0≤p≤10^6. 1≤k≤maxu⊆V(depu), 0≤p≤106.
思路
cost between two layers of nodes p 直接到达,Then you can connect.
But if you connect directly,Assume that two points, respectively n, m,Then the number of edges is n*m,边数很多.
Can it be less connected??
Create an imaginary point between the two layers,All nodes in the upper layer are connected to the virtual point with a by-direction edge,边权为 p;Connect a directed edge from the virtual point to all nodes in the lower layer,边权为 0.连边数 n+m.
注意是有向边!
Then the cost from any node in the upper layer to any node in the lower layer is still p,But less to build a multilateral!
This is the idea,A virtual point is established between the two layers that can be directly reached,Two layers of nodes connect edges to this virtual point,Then you can run the shortest way directly.
需要注意,input quantity arrives 5e6,要换scanf,best read.
Code
#include<bits/stdc++.h>
using namespace std;
#define Ios ios::sync_with_stdio(false),cin.tie(0)
#define int long long
#define PII pair<int,int>
#define pb push_back
#define fi first
#define se second
#define endl '\n'
static char buf[100000],*pa=buf,*pd=buf;
#define gc pa==pd&&(pd=(pa=buf)+fread(buf,1,100000,stdin),pa==pd)?EOF:*pa++
inline int read()
{
register int x(0);register char c(gc);
while(c<'0'||c>'9')c=gc;
while(c>='0'&&c<='9')x=(x<<1)+(x<<3)+(c^48),c=gc;
return x;
}
const int N = 1000010, mod = 1e9+7;
int T, n, m;
int a[N];
vector<PII> e[N*2];
int k, p, st, en;
int dep[N];
vector<int> v[N];
int maxdep;
int dist[N*2], f[N*2];
void bfs()
{
for(int i=1;i<=n;i++) dep[i] = 0;
dep[1] = 1;
queue<int> que;
que.push(1);
v[1].push_back(1);
while(que.size())
{
int x = que.front(); que.pop();
for(PII it : e[x])
{
int tx = it.fi;
if(dep[tx]) continue;
dep[tx] = dep[x] + 1;
v[dep[tx]].push_back(tx);
maxdep = max(maxdep, dep[tx]); //Maximum depth can be maintained,to reduce subsequent initialization and edge building
que.push(tx);
}
}
}
int dij()
{
for(int i=1;i<=2*n;i++) dist[i] = 1e18, f[i] = 0;
dist[st] = 0;
priority_queue<PII, vector<PII>, greater<PII> > que;
que.push({
0, st});
while(que.size())
{
int x = que.top().se; que.pop();
if(f[x]) continue;
f[x] = 1;
if(x == en) return dist[x];
for(auto it : e[x])
{
int tx = it.fi, dis = it.se;
if(dist[tx] > dist[x] + dis)
dist[tx] = dist[x] + dis, que.push({
dist[tx], tx});
}
}
return -1;
}
void init()
{
for(int i=1;i<=n;i++) v[i].clear();
for(int i=1;i<=2*n;i++) e[i].clear();
maxdep = 1;
}
signed main(){
T = read();
while(T--)
{
n = read();
init();
for(int i=1;i<n;i++)
{
int x, y, z;
x = read(), y = read(), z = read();
e[x].push_back({
y, z});
e[y].push_back({
x, z});
}
k = read(), p = read();
st = read(), en = read();
bfs();
for(int i=1;i<=n;i++)
{
int tx = i + k;
if(tx > maxdep) break; //It doesn't matter if it is greater than the maximum depth
for(int t : v[i]) e[t].push_back({
n+i, p});
for(int t : v[tx]) e[n+i].push_back({
t, 0});
}
printf("%lld\n", dij());
}
return 0;
}
经验
建立虚点,很妙的做法.
Also see an app:
If there are several starting points,several endpoints,Find the shortest distance from any starting point to any ending point.
At this time, if you do it simply, you will run n 次最短路,But you can create a virtual source point,Connect edges to all origins,权值为 0,Then it only takes one time to run the shortest path from this source.
很妙!
边栏推荐
猜你喜欢
【store商城项目01】环境准备以及测试
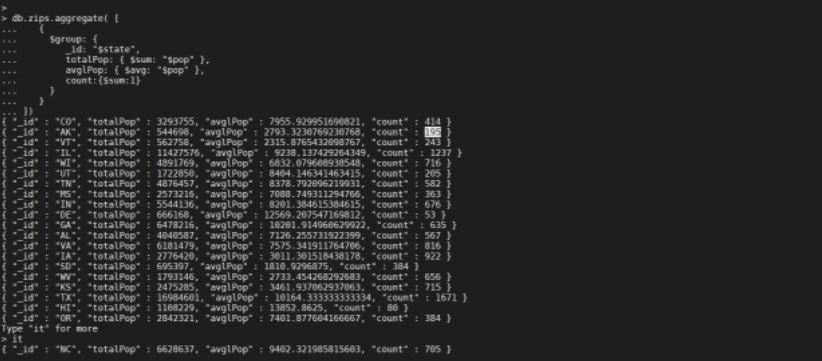
【详细教程】一文参透MongoDB聚合查询

2022 中国算力大会发布“创新先锋”优秀成果
How to find the cause of Fiori Launchpad routing errors by single-step debugging

SQL优化的一些建议,希望可以帮到和我一样被SQL折磨的你
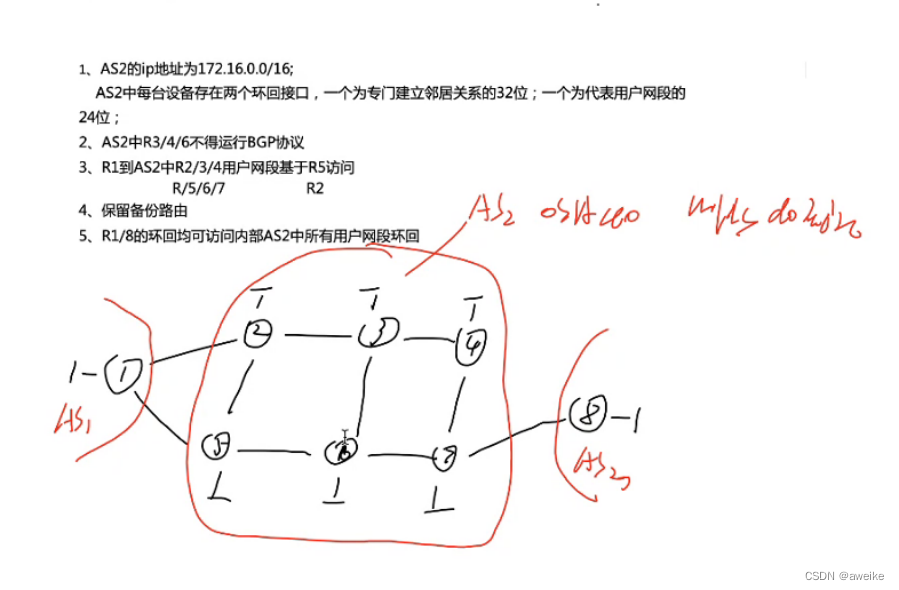
BGP实验(含MPLS)
The 600MHz band is here, will it be the new golden band?

Web3 security risks daunting?How should we respond?
nodejs installation and environment configuration
MySQL回表指的是什么
随机推荐
中原银行实时风控体系建设实践
快速入门EasyX图形编程
GraphQL背后处理及执行过程是什么
What warehouse management problems can WMS warehouse management system solve in the electronics industry?
Use nodejs switch version (no need to uninstall and reinstall)
redis中常见的问题(缓存穿透,缓存雪崩,缓存击穿,redis淘汰策略)
114. How to find the cause of Fiori Launchpad routing error by single-step debugging
字符串的排列
分析:Nomad Bridge黑客攻击的独特之处
iframe通信
Web3 security risks daunting?How should we respond?
互斥锁、读写锁、自旋锁,以及原子操作指令xaddl、cmpxchg的使用场景剖析
Deng Qinglin, Alibaba Cloud Technical Expert: Best Practices for Disaster Recovery across Availability Zones and Multiple Lives in Different Locations on the Cloud
ThreadLocal
typescript56-泛型接口
C语言 函数递归
Is there any jdbc link to Youxuan database documentation and examples?
typescript50 - type specification between cross types and interfaces
微服务的简单介绍
MATLAB三维绘图命令plot3入门