Calculation of time and space complexity (notes of runners)

Let's introduce efficiency first

Preface

Enter data structure and deep section C The status of will be updated later .

Efficiency introduction

Algorithm efficiency

** There are two kinds of algorithm efficiency analysis ： The first is time efficiency , The second is spatial efficiency .** Time efficiency is called time complexity ,

And spatial efficiency is called spatial complexity . Time complexity mainly measures the running speed of an algorithm , The spatial complexity is mainly

To measure the extra space required for an algorithm , In the early days of computer development , The storage capacity of the computer is very small . So for space

Complexity matters a lot . But after the rapid development of the computer industry , The storage capacity of the computer has reached a high level .

So now we don't need to pay special attention to the spatial complexity of an algorithm

Time efficiency

Definition of time complexity ： In computer science , The time complexity of the algorithm is a function , It quantitatively describes the running time of the algorithm . And the operation time is different in different hardware, so The number of times the basic operations in the algorithm are executed , Time complexity of the algorithm .

Spatial complexity

Calculation of common time complexity

Explain with examples

First of all, let's introduce some big O Progressive expression of

Big O Symbol （Big O notation）： Is a mathematical symbol used to describe the progressive behavior of a function

** Derivation is great O Order method : **

1、 With constant 1 Replace all the addition constants in runtime .

2、 In the modified run times function , Only the highest order terms .

3、 If the highest order term exists and is not 1, The constant multiplied by this item is removed . The result is big O rank .

In short, keeping the one that has the greatest impact on the number of runs and removing the multiplied number is generally the expression in the time complexity ( If the number of executions is constant, it is O(1)

Let's explain with examples

//  Please calculate Func1 How many times has the basic operation been performed ？
void Func1(int N)
{
    
    int count = 0;
    for (int i = 0; i < N; ++i)
    {
    
        for (int j = 0; j < N; ++j)
        {
    
            ++count;
        }
    }
    for (int k = 0; k < 2 * N; ++k)
    {
    
        ++count;
    }
    int M = 10;
    while (M--)
    {
    
        ++count;
    }
    printf("%d\n", count);
}

• First, in the first for There is a nested in the loop for The loop is executed N*N Time
• The second for In the loop 2*N Time
• In the end, there is a constant 10 Time

The total number of execution is N^2+2*N+10 Time

The second rule of our rules requires that only the highest end be kept ( And in N The expression that has the greatest impact on the result when changing ) And N^2 therefore Func1 The time complexity of is O(N^2)

In addition, sometimes our program time complexity has the best case and the worst case, how to express it

Such as :

The best situation : lookup 1 Time

The worst : lookup N Time

In practice, we generally focus on the worst-case operation of the algorithm . So the time complexity of the above example is O(N).

The complexity of binary search is obtained through the above principles

//  Calculation BinarySearch Time complexity of ？
int BinarySearch(int* a, int n, int x) 
{
    
    assert(a);
    int begin = 0;
    int end = n;
    while (begin < end)
    {
    
        int mid = begin + ((end - begin) >> 1);
        if (a[mid] < x)
            begin = mid + 1;
        else if (a[mid] > x)
            end = mid;
        else
            return mid;
    }
    return -1;
}

Binary search may get the value we want at one time, or it may need to search many times until the worst case , What is the number of worst cases ?

We set the maximum number of times as X

Every time the search fails, half of the search range will be subtracted , We can get such an expression by backward derivation

2^X = N therefore X = logN( Exactly, it should be log With 2 At the bottom of the N But because we need a formula, we call it... For short in the algorithm logN)

How to express the time complexity when there are two variables controlling the number of operations ?

Such as :

void Func3(int N, int M)
{
    
    int count = 0;
    for (int k = 0; k < M; ++k)
    {
    
        ++count;
    }
    for (int k = 0; k < N; ++k)
    {
    
        ++count;
    }
    printf("%d\n", count);
}

Yes M And then there is N , May be collectively referred to as O(N+M)

Of course, if conditions are given, such as M Far greater than N That's it O(M)

M and N It can be written as O(M) or O(N)

//  Calculation Func4 Time complexity of ？
void Func4(int N) 
{
    
    int count = 0;
    for (int k = 0; k < 100; ++k)
    {
    
        ++count;
    }
    printf("%d\n", count);
}

The number of execution is fixed and 100 So the time complexity is O(1)

Time complexity comparison chart

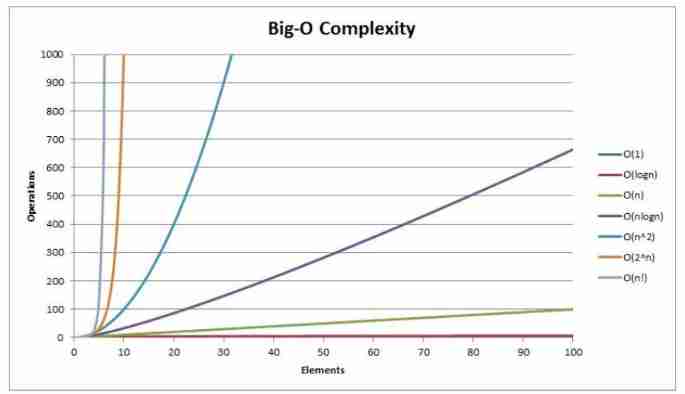
Calculation of spatial complexity

So spatial complexity is the number of variables . Spatial complexity calculation rules are basically similar to practical complexity , Also used Big O Progressive representation

Big O Symbol （Big O notation）： Is a mathematical symbol used to describe the progressive behavior of a function

The calculation method of space complexity is similar to that of time complexity , Are the worst calculations ( Maximum ) Complexity of case .

Explanation of previous examples :

//  Calculation BubbleSort Spatial complexity of ？
void BubbleSort(int* a, int n) 
{
    
	assert(a);
	for (size_t end = n; end > 0; --end)
	{
    
		int exchange = 0;
		for (size_t i = 1; i < end; ++i)
		{
    
			if (a[i - 1] > a[i])
			{
    
				Swap(&a[i - 1], &a[i]);
				exchange = 1;
			}
		}
		if (exchange == 0)
			break;
	}
}

We established int*a,int n,size_t end, int eschange,size_t i5 The two variables are similar to the establishment of time complexity constant

O(1)

Example 2:

//  Calculation Fibonacci Spatial complexity of ？
long long* Fibonacci(size_t n)
{
    
	if (n == 0)
		return NULL;
	long long* fibArray = (long long*)malloc((n + 1) * sizeof(long long));
	fibArray[0] = 0;
	fibArray[1] = 1;
	for (int i = 2; i <= n; ++i)
	{
    
		fibArray[i] = fibArray[i - 1] + fibArray[i - 2];
	}
	return fibArray;
}

We see long long* fibArray = (long long*)malloc((n + 1) * sizeof(long long));

We created longlong Type of N+1 And other constant variables

So the space complexity is zero O(N) ( Similar to using only the one that has the greatest impact on complexity )

Example 3:

//  Compute factorial recursion Factorial Spatial complexity of ？
long long Factorial(size_t N) 
{
    
	return N < 2 ? N : Factorial(N - 1) * N;
}

Every time we call the function, we will create a variable and size_t N But we called N Degree function and established N individual size_t N

So the space complexity is zero O(N)