[point cloud processing paper crazy reading frontier version 8] - pointview gcn: 3D shape classification with multi view point clouds

Abstract

• Capture part of the point cloud from multiple viewpoints around the object 3D shape classification
• Pointview-GCN have multi-level Of Graph Convolutional Networks (GCNs), With fine-to-coarse To aggregate the shape features of a single view point cloud , So as to achieve the right Geometric information of the object and Multi perspective relationship The purpose of coding
• The code can be found in the ：https://github.com/SMohammadi89/PointView-GCN PyTorch edition

1. introduction

• The point cloud data captured in real life are all part of the point cloud obtained from different perspectives
• Graph Convolutional Networks (GCNs) It is proved that it is right to Semantic relationship coding for feature aggregation The power of
• Pointview-GCN A method with multi-level GCNs Network of , Aggregate shape features from partial point clouds of multiple views , With fine-to-coarse Mining semantic relationships in adjacent views
• In different layers GCNs Inter join skip connection
• A new data set is proposed , This data set contains point cloud data from a single perspective

2. Related work

MVCNN Use max-pooling Aggregate features from different views , Finally, we get a global shape descriptor, The disadvantage is that The semantic relationship between multi view data is not considered .

View-GCN A new method based on view Graph convolution network , Capture structural relationships in data , But all of the above methods are to aggregate features on the image .

3. Method

• First, take multiple partial point data from different perspectives of the object
• utilize backbone Extract the features of each part of the point cloud
• Create a with $N$ Graph of nodes $G={\left\{v_i\right\}}_{i\in N}$, Pass the first $i$ Shape features of single view point cloud data $F_i$ Representation node $v_i$, among $\mathbf{F}={\left\{F_i\right\}}_{i\in N}$ yes $G$ All node characteristics of ,$v_p$ yes $v_i$ Adjacent points of (kNN),$G$ The adjacency matrix of is $\mathbf{A}$

It is proposed that the feature aggregation of network includes multiple level Of GCNs, Pictured 2 Shown ,level The optimal number of $M$ Determined by experiment .

In the $j$ individual level in , For the input $G^j$ perform graph convolution operation , Update node characteristics $F_i$, Followed by an optional view-sampling, Get smaller graph $G^{j+1}$,$G^{j+1}$ It contains $G^j$ The most important view information .

$G^{j+1}$ It is put into the... As input again $j+1$ individual level in .

3.1. Graph convolution and Selective View Sampling

In the $j$ individual level in , Perform the following three operations ：

1. local graph convolution
2. non-local message passing
3. selective view sampling (SVS)

Local graph convolution

Consider nodes $v_i^j$ And its adjacent nodes ,local graph convolution Update the node through the following formula $v_i^j$ Characteristics of ：
$${\tilde{\mathbf{F}}}^j=\mathcal{L}\left({\mathbf{A}}^j{\mathbf{F}}^j{\mathbf{W}}^j;{\alpha }^j\right)$$
among $\mathcal{L}(\cdot )$ Express LeakyReLU operation ,${\alpha }^j$ and ${\mathbf{W}}^j$ Is the weight matrix .

non-local message passing

Then we have to pass non-local message passing to update ${\tilde{\mathbf{F}}}^j$, consider $G^j$ Long distance relationship between all nodes in . Every node $v_i$ First, update its state to the edge between adjacent vertices ：

$$m_{i,p}^j=\mathcal{R}{\left({\tilde{F}}_i^j,{\tilde{F}}_p^j;{\beta }^j\right)}_{i,p\in N^j}$$

among $\mathcal{R}(\cdot )$ Represents the... Between a pair of views relation function,${\beta }^j$ yes related parameters.

Then update the feature of the vertex by the following formula ：
$${\tilde{F}}_i^j=\mathcal{C}\left({\tilde{F}}_i^j,\sum _{p=1,p\ne i}^{N_j}{m}_{i,p}^j;{\gamma }^j\right)$$
among $\mathcal{C}(\cdot )$ yes combination function, ${\gamma }^j$ yes related parameters.

Through non-local message passing after , The feature is updated by considering the relationship of the whole graph .

selective view sampling (SVS)

1. Use Farthest Point Sampling (FPS) Yes $G^j$ Take the next sample
2. Each node after down sampling $v_i$ The nearest neighbor of ${\mathbf{V}}_i^j$ in , Use view-selector choice softmax The node with the largest function response
3. take coarsened $G^{j+1}$ And updated ${\mathbf{F}}^{j+1}$ Put it on the next layer to continue processing

3.2. Multi-level feature aggregation and training loss

In each layer graph convolution after , All have one floor max-pooling It works on ${\mathbf{F}}^j$ On , The goal is to get every level Global shape feature on $F_{\text{global }}$.

The final global shape feature $F_{\text{global }}$ It's all level Middle quilt pool Stitching of back features .

From the first floor convolution level To the last floor convolution level Added a residual connection, Avoid when GCNs level The increase in the number of leads to the disappearance of the gradient .

Training losses consist of two elements , Global shape loss $L_{\text{global }}$ and selective-view Shape loss $L_{\text{selective }}$ ：
$$\begin{array}{rl}L=& L_{\text{global }}\left(\mathcal{S}\left(F_{\text{global }}\right),y\right)+\\ & \sum _{j=1}^M\sum _{i=1}^{N^{j+1}}\sum _{v_s\in {\mathbf{V}}_i^j}{L}_{\text{selective }}\left(\mathcal{V}\left(F_s^j;{\theta }^j\right),y\right)\end{array}$$
among $L_{\text{global }}$ It's cross entropy loss ,$\mathcal{S}$ It includes the full connection layer and softmax Function classifier ,$y$ Is shape classification .$L_{\text{selective }}$ Is used for view selector Cross entropy of , Ensure that the selected view can recognize shape shape classification .$\mathcal{V}(\cdot )$ Is used for view selector Function of , Parameter is ${\theta }^j$.$F_s^j$ Is the node after down sampling .

During the training , Only $L_{\text{global }}$ Participate in .

4. experiment

Dataset generation

ModelNet40 Contains 12311 individual model,40 Categories
ScanObjectNN Contains 2909 individual model,15 Categories
Based on this, we build 4 Data sets ：Model-D, Model-H, Scan-D and Scan-H
D Represents icosahedral （20 individual viewpoints）,H It means hemisphere （12 individual viewpoints）

Implementation details

backbone：PointNet++ /DGCNN

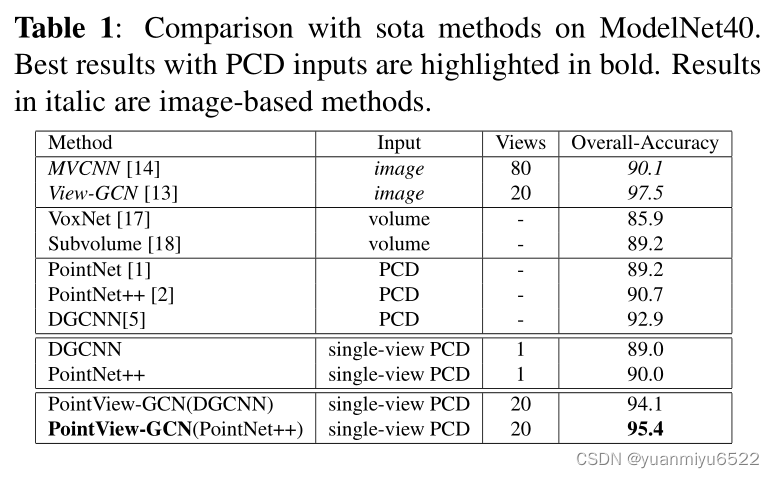
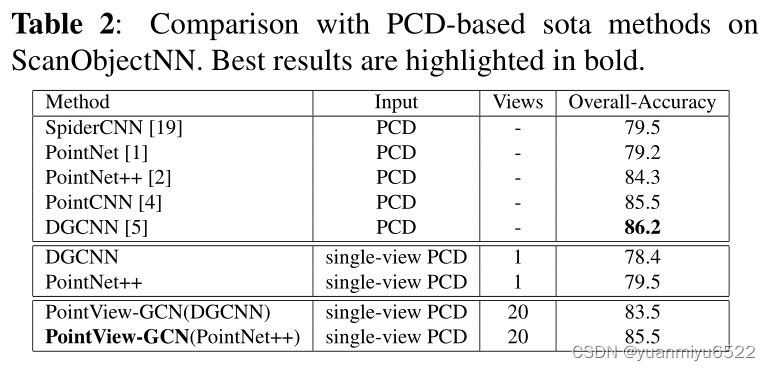
4.1. Comparison against state-of-the-art methods

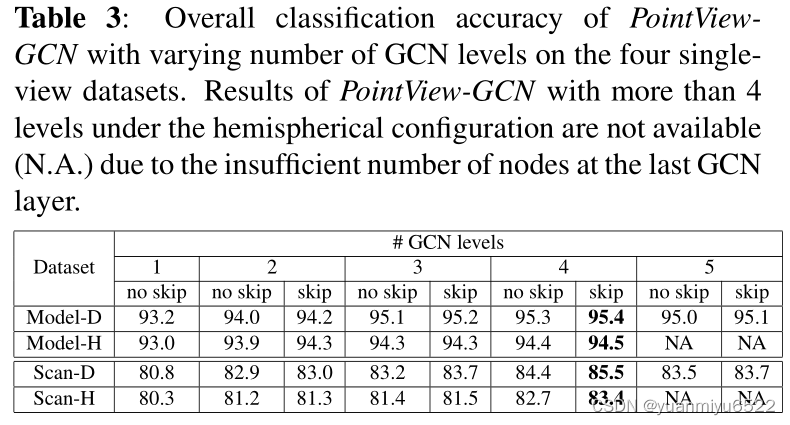
4.2. Ablation studies

Effects of levels of GCN and skip connection

Effects of number of input views

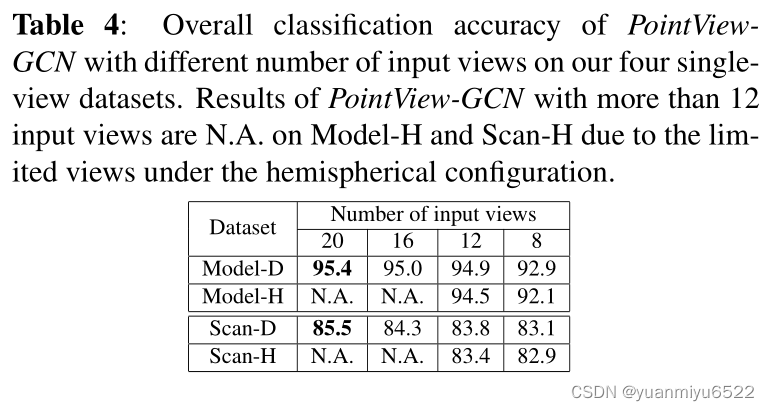
Hemispherical angle of view design accuracy is not as good as icosahedral , Maybe it's because the bottom doesn't collect enough information .

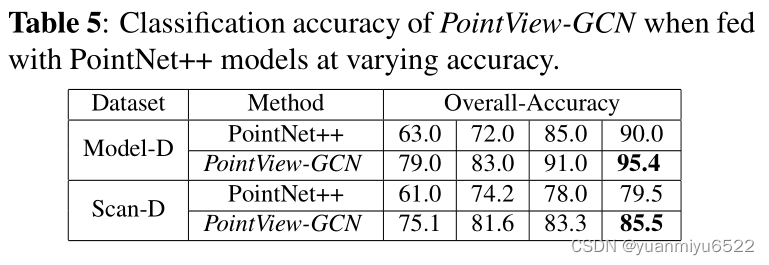
Effects of PointNet++ models of varying classification accuracy