当前位置:网站首页>Petri net-2, directed net
Petri net-2, directed net
2022-08-03 13:55:00 【Old stubborn and cute】
petri网
2、有向网
三元组 N = ( S , T ; F ) N=(S,T;F) N=(S,T;F) directed net,如果
| 表达式 | 含义 |
|---|---|
| S ⋃ T ≠ ∅ S \bigcup T \neq \emptyset S⋃T=∅ | 非空 |
| ⋀ S ⋂ T ≠ ∅ \bigwedge S \bigcap T \neq \emptyset ⋀S⋂T=∅ | 两类元素 |
| ⋀ F ⊆ S × T ⋃ T × S \bigwedge F \subseteq S \times T \bigcup T \times S ⋀F⊆S×T⋃T×S | 两种关系 |
| ⋀ d o m ( F ) ⋃ c o d ( F ) = S ⋃ T \bigwedge dom(F) \bigcup cod(F) = S \bigcup T ⋀dom(F)⋃cod(F)=S⋃T | No isolated elements |
其中:
- d o m ( F ) = { x ∣ ∃ y : ( x , y ) ∈ F } dom(F) = \{x| \exists y:(x,y)\in F \} dom(F)={ x∣∃y:(x,y)∈F}
- c o d ( F ) = { y ∣ ∃ x : ( x , y ) ∈ F } cod(F) = \{y| \exists x:(x,y)\in F \} cod(F)={ y∣∃x:(x,y)∈F}
例1:
- S = { c , x , q , d } S=\{c,x,q,d\} S={ c,x,q,d}
- T = { c x , x q , q d , d c } T=\{cx,xq,qd,dc\} T={ cx,xq,qd,dc}
- F = { ( c , c x ) , ( c x , x ) , ( x , x q ) , ( x q , q ) , ( q , q d ) , ( q d , d ) , ( d , d c ) , ( d c , c ) } F=\{(c,cx),(cx,x),(x,xq),(xq,q),(q,qd),(qd,d),(d,dc),(dc,c)\} F={(c,cx),(cx,x),(x,xq),(xq,q),(q,qd),(qd,d),(d,dc),(dc,c)}
- N 1 = { S , T ; F } N_1=\{S,T;F\} N1={ S,T;F}
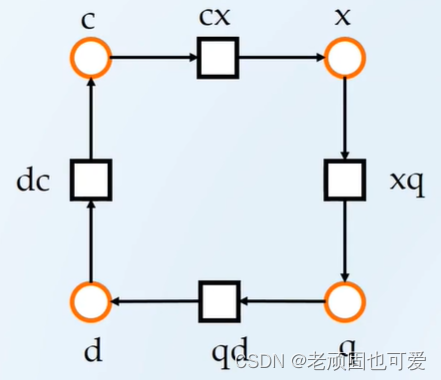
例2:
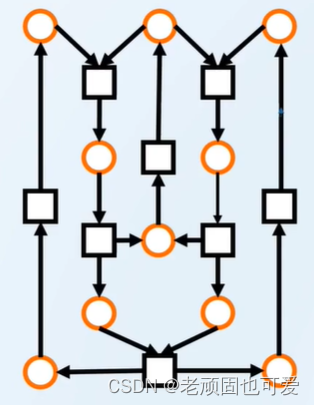
2.1 基本元素
- S S S 元素:
 place 库所
place 库所 - T T T 元素:
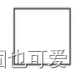 transition 变迁(不是迁移,more than just moving,This qualitative change,variable)
transition 变迁(不是迁移,more than just moving,This qualitative change,variable) - F:
 flow relation 流关系
flow relation 流关系
2.2 Expression comparison
- semi-formal definition:易读,suitable for written communication
- 形式化定义:suitable for introducing mathematical methods,Facilitate automatic processing
- 图形表示:直观 便于交流,Highlight the reticular structure,No need to name elements when communicating face-to-face
例3:
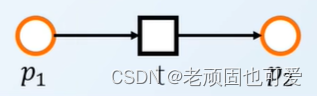
- 上图是 N = ( { S 1 , S 2 } , { t } ; { ( S 1 , t ) , ( t , S 2 ) } ) N=(\{S_1,S_2\},\{t\};\{(S_1,t),(t,S_2)\}) N=({ S1,S2},{ t};{(S1,t),(t,S2)}) A graphical representation of the?
- in the sense of isomorphism,是(同构:One-to-one correspondence between like elements,包括 F F F )
例4:

- Is this a directed network?
- 可以看成一个,也可以看成两个.The definition does not clearly specify whether or not to connect.
- 但是,Since the two parts are not connected,Why study together?This is triggered from the actual application.
2.3 连通性

弱连通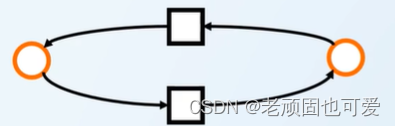
强连通,Remove an edge and still connect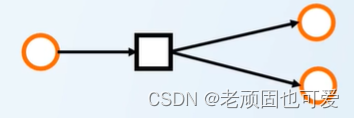
不连通,The last two no connection
2.4 Simple net、简单网
Do directed nets allow the following structure??

不单纯(单纯性)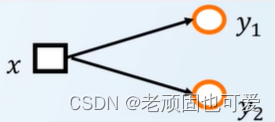
不简单(简单性)
repeating arc,不能出现
2.4.1 术语:前集、后集
X = S ⋃ T X = S \bigcup T X=S⋃T node set element set of directed net
x , y ∈ X f ( x ) = { . x = { y ∣ ( y , x ) ∈ F } , x the first episode of x . = { y ∣ ( x , y ) ∈ F } , x after the episode x,y \in X \\ f(x)=\left\{ \begin{aligned} ^.x & = & \{y|(y,x)\in F\} & , &xthe first episode of \\ x^. & = & \{y|(x,y)\in F\} & , &xafter the episode \end{aligned} \right. x,y∈Xf(x)={ .xx.=={ y∣(y,x)∈F}{ y∣(x,y)∈F},,xthe first episode ofxafter the episode
2.4.2 Simple net、简单网、连通网
2.4.2.1 Simple net definition
∀ x ∈ X : . x ∩ x . ≠ ∅ \forall x \in X:\\ ^.x \cap x^. \neq \empty ∀x∈X:.x∩x.=∅
2.4.2.2 Simple net definition
∀ x , y ∈ X : . x = . y ⋀ x . = y . ⋀ x ≠ y \forall x,y \in X:\\ ^.x=^.y\bigwedge x^.=y^.\bigwedge x\neq y ∀x,y∈X:.x=.y⋀x.=y.⋀x=y
2.4.2.3 连通图定义
∀ x , y ∈ X : ( x , y ) ∈ ( F ∪ F − 1 ) + 其中 F − 1 = { ( a , b ) ∣ ( b , a ) ∈ F } \forall x,y \in X:\\ (x,y)\in (F\cup F^{-1})^+\\ 其中 F^{-1}=\{(a,b)|(b,a)\in F\} ∀x,y∈X:(x,y)∈(F∪F−1)+其中F−1={(a,b)∣(b,a)∈F}
2.4.2.4 Repeating Arc Problem
Not allowed to repeat the arc
2.4.2.5 Dual network and reciprocal network
N = ( S , T ; F ) , N ′ = ( S ′ , T ′ ; F ′ ) 为有向网 N 和 N ′ For the dual network , 如果 S ′ = T ⋀ T ′ = S ⋀ F ′ = F N 和 N ′ reciprocal network , 如果 S ′ = S ⋀ T ′ = T ⋀ F ′ = F − 1 N=(S,T;F), N'=(S',T';F') 为有向网\\ N和N'For the dual network,如果 S'=T\bigwedge T'=S\bigwedge F'=F\\ N和N'reciprocal network,如果 S'=S\bigwedge T'=T\bigwedge F'=F^{-1}\\ N=(S,T;F),N′=(S′,T′;F′)为有向网N和N′For the dual network,如果S′=T⋀T′=S⋀F′=FN和N′reciprocal network,如果S′=S⋀T′=T⋀F′=F−1


The following two network is the same network,同为 N = ( { S 1 , S 2 } , { t } ; { ( S 1 , t ) , { t , S 2 } } ) N=(\{S_1,S_2\},\{t\};\{(S_1,t),\{t,S_2\}\}) N=({ S1,S2},{ t};{(S1,t),{ t,S2}}) 的图示

2.4.3 cable network & Infinite network
A directed net can have a finite number of elements,There can also be an uncountable finite number of elements ∣ S ∪ T ∣ < ∞ |S\cup T|<\infty ∣S∪T∣<∞
- cable network
- 人造系统:能力有限
- 自然规律(like the changing seasons):局部观察
- Infinite network
- Documenting natural change that never ends
- 理论研究(图灵机)
2.5 出现网
record what happened
例5:

2.6 Basic Concept Definition Golden Rule
not necessary to include,it is necessary not to include
2.6.1 Directed net definition does not contain
- 连通性
- 单纯性
- 简洁性
- 有限性
2.6.2 Directed network concept
- Basic concepts are concise
- Flexibility to introduce subsequent concepts
边栏推荐
猜你喜欢
随机推荐
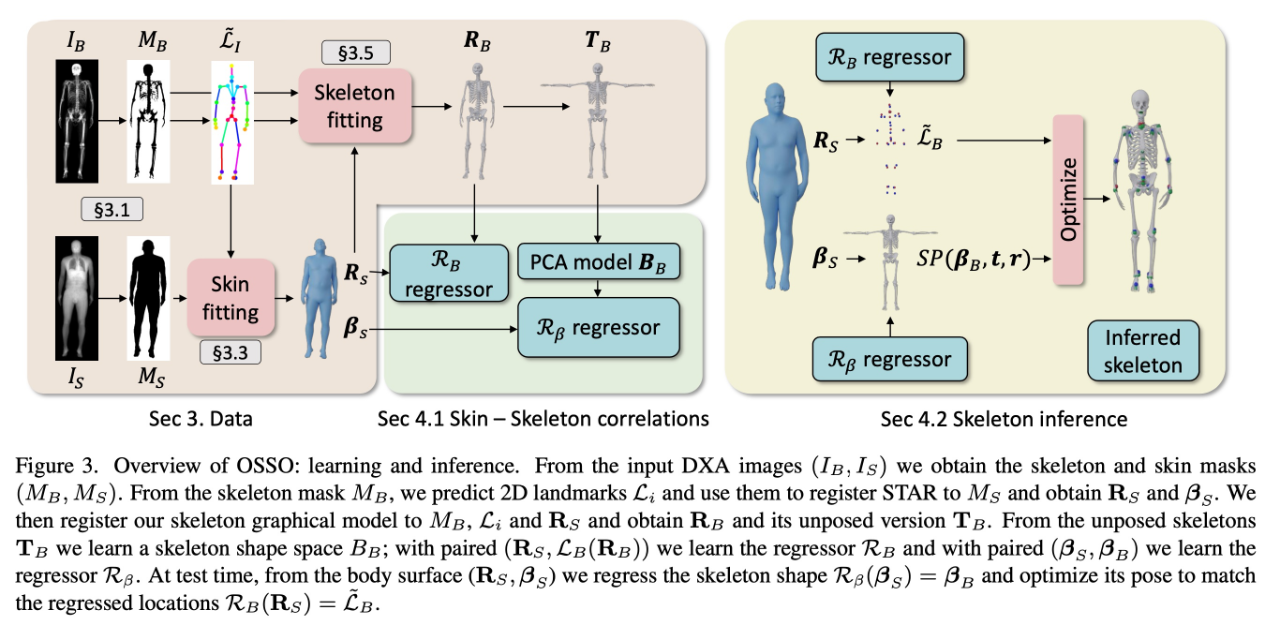
CVPR 2022 | 从人体网格预测骨架,是真正的生理学骨架!
[web penetration] detailed explanation of CSRF vulnerability
PyTorch framework to train linear regression model (CPU and GPU environment)
细胞图像数据的主动学习
PCL 点云按时间进行分段
15 years of software architect experience summary: In the ML field, 5 pits that beginners have stepped on
使用Typora+EasyBlogImageForTypora写博客,无图床快速上传图片
An animation optimization of traditional guide layer animation
Golang channel channel
Nanoprobes EnzMet - 酶金相相关介绍及应用
【深度学习中的激活函数的整理与使用总结】
Golang 结构体&方法
Graphic animation and button animation of an animation basic component
数字孪生的4个最佳实践
[R] Use grafify for statistical plotting, ANOVA, intervention comparisons, and more!
[Microservice] Multi-level cache
[A summary of the sorting and use of activation functions in deep learning]
如何让history历史记录前带时间戳
PyTorch构建分类网络模型(Mnist数据集,全连接神经网络)
The maximum number of sliding window