当前位置:网站首页>[pyg] understand the messagepassing process, GCN demo details
[pyg] understand the messagepassing process, GCN demo details
2022-07-03 03:09:00 【LittleSeedling】
List of articles
Reference resources :
PyG utilize MessagePassing Realization GCN( understand pyG The underlying logic of )
PyG official demo GCN
PyG Information transmission mechanism of
PyG Provides Information transmission ( Neighbor aggregation ) Framework model of operation .
x i k = γ k ( x i k − 1 , □ j ∈ N ( i ) ϕ ( x i k − 1 , x j k − 1 , e j , i ) ) x_i^k = \gamma^k(x_i^{k-1}, \square_{j \in \mathcal{N}(i)} \phi(x_i^{k-1},x_j^{k-1},e_{j,i})) xik=γk(xik−1,□j∈N(i)ϕ(xik−1,xjk−1,ej,i))
among ,
□ \square □ Express It's very small 、 The arrangement does not change Function of , for instance sum、mean、max
γ \gamma γ and ϕ \phi ϕ Express It's very small Function of , for instance MLP
stay propagate in , Will call in turn message,aggregate,update function .
among ,message Is in the formula ϕ \phi ϕ part aggregate Is in the formula □ \square □ part update Is in the formula γ \gamma γ part
MessagePassing Class
PyG Use MessagePassing Class as an implementation Information transmission Base class of mechanism . We just need to inherit it .
GCN demo
GCN The information transmission formula is as follows :
x i k = ∑ j ∈ i ∪ { i } 1 d e g ( i ) ⋅ d e g ( j ) ⋅ ( Θ T ⋅ x j k − 1 ) x_i^k = \sum_{j \in \mathcal{i} \cup \{i\}} {1 \over \sqrt{\mathrm{deg}(i)} \cdot \sqrt{\mathrm{deg}(j)} } \cdot (\Theta^T \cdot x_j^{k-1}) xik=j∈i∪{ i}∑deg(i)⋅deg(j)1⋅(ΘT⋅xjk−1)
notes :GCN Is running on the Undirected graph Upper .
1. Import header file
from typing import Optional
from torch_scatter import scatter
import torch
import numpy as np
import random
import os
from torch import Tensor
from torch_geometric.nn import MessagePassing
from torch_geometric.utils import add_self_loops, degree
2. Constructors
class GCNConv(MessagePassing):
def __init__(self, in_channels, out_channels):
super().__init__(aggr='add') # "Add" aggregation (Step 5).
self.lin = torch.nn.Linear(in_channels, out_channels)
Defining classes GCNConv Inherit MessagePassing.
aggr Defined Aggregate functions The role of . here add Indicates accumulation .
Of course , We can also rewrite aggregate Method , From definition Aggregate functions .
The linear transformation layer is defined lin, That is... In the formula Θ \Theta Θ. however , Unlike the formula , there lin Yes, there is bias bias Of .
3. Forward propagation forward
def forward(self, x, edge_index):
# x.shape == [N, in_channels]
# edge_index.shape == [2, E]
# Step 1: Add self-loops to the adjacency matrix.
edge_index, _ = add_self_loops(edge_index, num_nodes=x.size(0))
# Step 2: Linearly transform node feature matrix.
x = self.lin(x) # x = lin(x)
# Step 3: Compute normalization.
row, col = edge_index # row, col is the [out index] and [in index]
deg = degree(col, x.size(0), dtype=x.dtype) # [in_degree] of each node, deg.shape = [N]
deg_inv_sqrt = deg.pow(-0.5)
deg_inv_sqrt[deg_inv_sqrt == float('inf')] = 0
norm = deg_inv_sqrt[row] * deg_inv_sqrt[col] # deg_inv_sqrt.shape = [E]
# Step 4-5: Start propagating messages.
return self.propagate(edge_index, x=x, norm=norm)
Definition Neural network Forward propagation The process .
# Step 1: Add self-loops to the adjacency matrix.
edge_index, _ = add_self_loops(edge_index, num_nodes=x.size(0))
Add self ring .
# Step 2: Linearly transform node feature matrix.
x = self.lin(x) # x = lin(x)
Calculation Θ ⋅ x \Theta \cdot x Θ⋅x
# Step 3: Compute normalization.
row, col = edge_index # row, col is the [out index] and [in index]
deg = degree(col, x.size(0), dtype=x.dtype) # [in_degree] of each node, deg.shape = [N]
deg_inv_sqrt = deg.pow(-0.5)
deg_inv_sqrt[deg_inv_sqrt == float('inf')] = 0
norm = deg_inv_sqrt[row] * deg_inv_sqrt[col] # deg_inv_sqrt.shape = [E]
Calculation coefficient , That is... In the formula
1 d e g ( i ) ⋅ d e g ( j ) {1 \over \sqrt{\mathrm{deg}(i)} \cdot \sqrt{\mathrm{deg}(j)} } deg(i)⋅deg(j)1
It's a little hard to understand . According to The shape of the tensor To understand .
row Represents the vertex of the edge ,col Represents the vertex of the incoming edge .
notes :PyG It supports directed graphs , therefore
(0,1), (1,0)Together represent an edge in an undirected graph .
degree Calculation The degree of entering the vertex . but , because GCN Running on an undirected graph , Actually Number of vertices == Number of vertices .
deg_inv_sqrt[deg_inv_sqrt == float('inf')] = 0 Set the degree to 0 Remove the node of , Because they are infinite .
The final result is norm It means , The degree product of two nodes on the edge . namely , Each edge represents 1 d e g ( i ) ⋅ d e g ( j ) {1 \over \sqrt{\mathrm{deg}(i)} \cdot \sqrt{\mathrm{deg}(j)} } deg(i)⋅deg(j)1 A weight coefficient .
4. message
def message(self, x_i, x_j, norm):
# x_j ::= x[edge_index[0]] shape = [E, out_channels]
# x_i ::= x[edge_index[1]] shape = [E, out_channels]
# norm.view(-1, 1).shape = [E, 1]
# Step 4: Normalize node features.
return norm.view(-1, 1) * x_j
Definition Information transfer function .
Some students will ask ,
x_i, x_jWhere did it come from ?
PyG For us .
among ,MessagePassingDefault The flow of informationflowbysource_to_target. If there are edges(0,1), that The flow of information by0->1.x_jNamelysourcespot ,x_iNamelytargetspot .
norm.view(-1, 1) * x_j, take The weight on the edge Multiply source The characteristics of the dot . That's it 1 d e g ( i ) ⋅ d e g ( j ) ⋅ ( Θ T ⋅ x j k − 1 ) {1 \over \sqrt{\mathrm{deg}(i)} \cdot \sqrt{\mathrm{deg}(j)} } \cdot (\Theta^T \cdot x_j^{k-1}) deg(i)⋅deg(j)1⋅(ΘT⋅xjk−1).
5. aggregate
def aggregate(self, inputs: Tensor, index: Tensor,
ptr: Optional[Tensor] = None,
dim_size: Optional[int] = None) -> Tensor:
# The first parameter cannot be changed
# index ::= edge_index[1]
# dim_size ::= [number of node]
# Step 5: Aggregate the messages.
# out.shape = [number of node, out_channels]
out = scatter(inputs, index, dim=self.node_dim, dim_size=dim_size)
return out
Definition Aggregate functions .
Actually , To this step We don't have to write , Because of the previous aggr="add" That's enough .
index Parameters from PyG Provide , by Enter the number of the vertex .torch_scatter.scatter function To put it simply , Is to put Same number Properties of [ Add up 、 Ask for the biggest 、 Find the minimum ] Get together .
The picture below is ,scatter Ask for the biggest .

See :
pytorch:torch_scatter.scatter_max
torch.scatter And torch_scatter Library usage sorting
6. update
def update(self, inputs: Tensor, x_i, x_j) -> Tensor:
# The first parameter cannot be changed
# inputs ::= aggregate.out
# Step 6: Return new node embeddings.
return inputs
Use what you get Information , Update the information of the current node .
inputs by Update the information obtained , In fact, that is aggregate Output .
update Corresponding Formula γ \gamma γ .
Be careful : The first parameter by
aggregateOutput . Changeable name , But you can't change the position .
complete GCN demo Code
from typing import Optional
from torch_scatter import scatter
import torch
import numpy as np
import random
import os
from torch import Tensor
from torch_geometric.nn import MessagePassing
from torch_geometric.utils import add_self_loops, degree
class GCNConv(MessagePassing):
def __init__(self, in_channels, out_channels):
super().__init__(aggr='add') # "Add" aggregation (Step 5).
self.lin = torch.nn.Linear(in_channels, out_channels)
def forward(self, x, edge_index):
# x has shape [N, in_channels]
# edge_index has shape [2, E]
# Step 1: Add self-loops to the adjacency matrix.
edge_index, _ = add_self_loops(edge_index, num_nodes=x.size(0))
# Step 2: Linearly transform node feature matrix.
x = self.lin(x) # x = lin(x)
# Step 3: Compute normalization.
row, col = edge_index # row, col is the [out index] and [in index]
deg = degree(col, x.size(0), dtype=x.dtype) # [in_degree] of each node, deg.shape = [N]
deg_inv_sqrt = deg.pow(-0.5)
deg_inv_sqrt[deg_inv_sqrt == float('inf')] = 0
norm = deg_inv_sqrt[row] * deg_inv_sqrt[col] # deg_inv_sqrt.shape = [E]
# Step 4-6: Start propagating messages.
return self.propagate(edge_index, x=x, norm=norm)
def message(self, x_i, x_j, norm):
# x_j ::= x[edge_index[0]] shape = [E, out_channels]
# x_i ::= x[edge_index[1]] shape = [E, out_channels]
print("x_j", x_j.shape, x_j)
print("x_i: ", x_i.shape, x_i)
# norm.view(-1, 1).shape = [E, 1]
# Step 4: Normalize node features.
return norm.view(-1, 1) * x_j
def aggregate(self, inputs: Tensor, index: Tensor,
ptr: Optional[Tensor] = None,
dim_size: Optional[int] = None) -> Tensor:
# The first parameter cannot be changed
# index ::= edge_index[1]
# dim_size ::= [number of node]
print("agg_index: ",index)
print("agg_dim_size: ",dim_size)
# Step 5: Aggregate the messages.
# out.shape = [number of node, out_channels]
out = scatter(inputs, index, dim=self.node_dim, dim_size=dim_size)
print("agg_out:",out.shape,out)
return out
def update(self, inputs: Tensor, x_i, x_j) -> Tensor:
# The first parameter cannot be changed
# inputs ::= aggregate.out
# Step 6: Return new node embeddings.
print("update_x_i: ",x_i.shape,x_i)
print("update_x_j: ",x_j.shape,x_j)
print("update_inputs: ",inputs.shape, inputs)
return inputs
def set_seed(seed=1029):
random.seed(seed)
os.environ['PYTHONHASHSEED'] = str(seed) # To prohibit hash randomization , Make the experiment repeatable
np.random.seed(seed)
torch.manual_seed(seed)
torch.cuda.manual_seed(seed)
torch.cuda.manual_seed_all(seed) # if you are using multi-GPU.
torch.backends.cudnn.benchmark = False
torch.backends.cudnn.deterministic = True
if __name__ == '__main__':
set_seed(0)
# x.shape = [5, 2]
x = torch.tensor([[1,2], [3,4], [3,5], [4,5], [2,6]], dtype=torch.float)
# edge_index.shape = [2, 6]
edge_index = torch.tensor([[0,1,2,3,1,4], [1,0,3,2,4,1]])
print("num_node: ",x.shape[0])
print("num_edge: ",edge_index.shape[1])
in_channels = x.shape[1]
out_channels = 3
gcn = GCNConv(in_channels, out_channels)
out = gcn(x, edge_index)
print(out)
Hold on Random number seed after , Multiple runs , better Compare And understand .
边栏推荐
- Kubernetes family container housekeeper pod online Q & A?
- Source code analysis | layout file loading process
- VS 2019 配置tensorRT生成engine
- I2C 子系统(三):I2C Driver
- How to make backgroundworker return an object
- 基于Qt的yolov5工程
- Check log4j problems using stain analysis
- Vs 2019 configuration du moteur de génération de tensorrt
- 用docker 连接mysql的过程
- Andwhere multiple or query ORM conditions in yii2
猜你喜欢
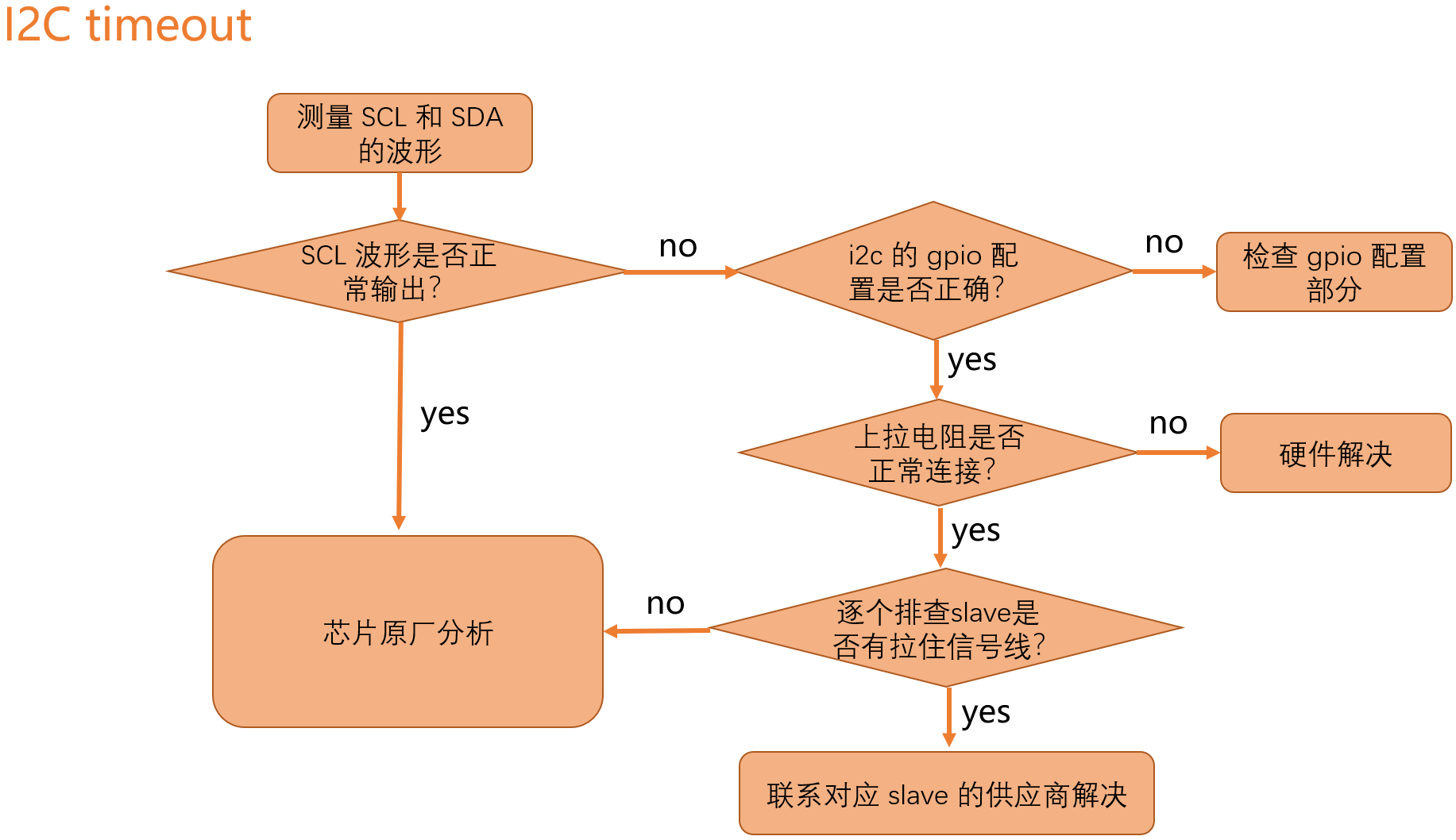
I2C 子系统(四):I2C debug

Kubernetes family container housekeeper pod online Q & A?

Idea set method call ignore case

Thunderbolt Chrome extension caused the data returned by the server JS parsing page data exception

Three. JS local environment setup
![[principles of multithreading and high concurrency: 1_cpu multi-level cache model]](/img/c7/6b5ab4ff7379bfccff7cdbb358ff8f.jpg)
[principles of multithreading and high concurrency: 1_cpu multi-level cache model]

函数栈帧的创建与销毁

Privatization lightweight continuous integration deployment scheme -- 01 environment configuration (Part 2)

el-tree搜索方法使用
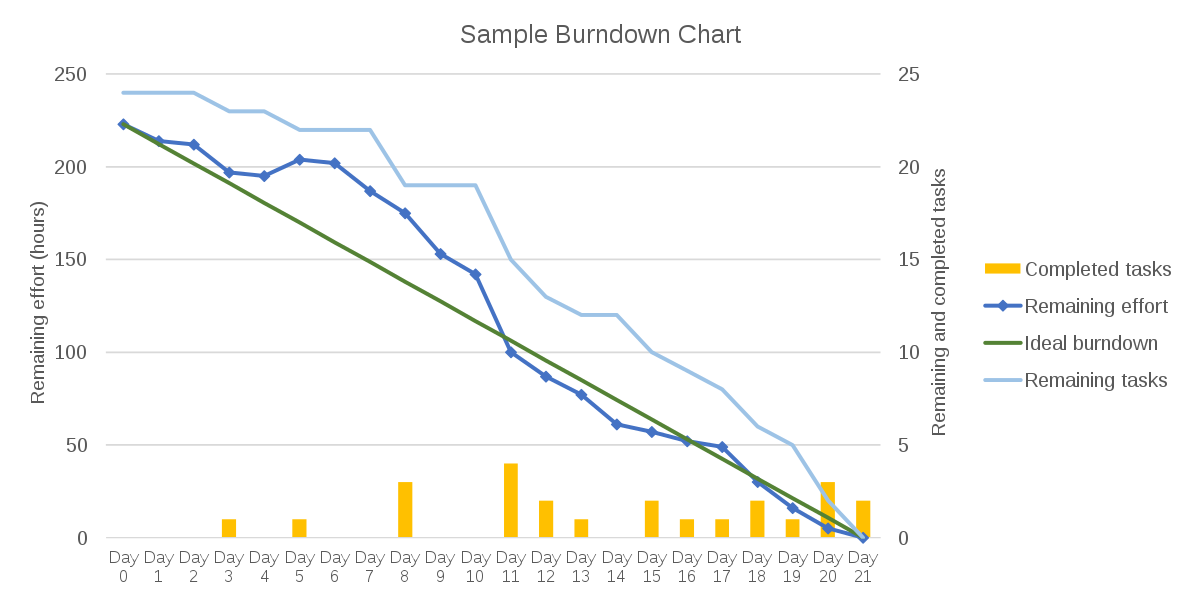
Agile certification (professional scrum Master) simulation exercise-2
随机推荐
Check log4j problems using stain analysis
I2C subsystem (III): I2C driver
Three.js本地环境搭建
Gavin teacher's perception of transformer live class - rasa project's actual banking financial BOT Intelligent Business Dialogue robot architecture, process and phenomenon decryption through rasa inte
Basic information of Promethus (I)
[principles of multithreading and high concurrency: 1_cpu multi-level cache model]
Use optimization | points that can be optimized in recyclerview
Destroy the session and empty the specified attributes
力扣------网格中的最小路径代价
当lambda没有输入时,是何含义?
C language beginner level - pointer explanation - paoding jieniu chapter
【富瀚6630编码存录像,用rtsp服务器及时间戳同步实现vlc观看录像】
TCP 三次握手和四次挥手机制,TCP为什么要三次握手和四次挥手,TCP 连接建立失败处理机制
How to return ordered keys after counter counts the quantity
函数栈帧的创建与销毁
Idea format code idea set shortcut key format code
I2C 子系統(四):I2C debug
Add some hard dishes to the interview: how to improve throughput and timeliness in delayed task scenarios!
MySql实战45讲【索引】
Cron表达式介绍