当前位置:网站首页>198. House raiding
198. House raiding
2022-07-04 06:01:00 【mrbone9】
Address :
Power button 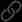 https://leetcode-cn.com/problems/house-robber/ subject :
https://leetcode-cn.com/problems/house-robber/ subject :
You are a professional thief , Plan to steal houses along the street . There is a certain amount of cash in every room , The only restriction on your theft is that adjacent houses are equipped with interconnected anti-theft systems , If two adjacent houses are broken into by thieves on the same night , The system will automatically alarm .
Given an array of non negative integers representing the storage amount of each house , Count you Without triggering the alarm , The maximum amount that can be stolen overnight .
Example 1:
| Input :[1,2,3,1] Output :4 explain : Steal 1 House No ( amount of money = 1) , And then steal 3 House No ( amount of money = 3). Maximum amount stolen = 1 + 3 = 4 . |
Example 2:
| Input :[2,7,9,3,1] Output :12 explain : Steal 1 House No ( amount of money = 2), Steal 3 House No ( amount of money = 9), Then steal 5 House No ( amount of money = 1). Maximum amount stolen = 2 + 9 + 1 = 12 . |
Tips :
| 1 <= nums.length <= 100 0 <= nums[i] <= 400 |
source : Power button (LeetCode)
link :https://leetcode-cn.com/problems/house-robber
Copyright belongs to the network . For commercial reprint, please contact the official authority , Non-commercial reprint please indicate the source .
Ideas :
Adopt the idea of dynamic programming
Suppose the current house is i, that dp[i] Indicates the total amount of the stolen house
dp[i] Your choice depends on :
1. Current house selection ,i-1 You can't choose a house ,dp[i] = dp[i-2] + nums[i]
2. The current house is not selected , It depends on dp[i-1] Value
Maximization is max(dp[i-1], dp[i-2] + nums[i])
Initial value :
dp[0] = nums[0] No choice
dp[1] = max(nums[0], nums[1]) A choice
Method 1 、 Dynamic programming
#define max(a,b) ( (a) > (b) ? (a) : (b) )
int rob(int* nums, int numsSize){
int i;
int dp[101]={0};
dp[0] = nums[0];
for(i=1; i<numsSize; i++)
{
if(i == 1)
dp[i] = max(nums[0], nums[1]);
else
dp[i]= max(dp[i-1], dp[i-2]+nums[i]);
}
return dp[numsSize - 1];
}边栏推荐
- 724. Find the central subscript of the array
- Canoe panel learning video
- [Chongqing Guangdong education] electronic circuit homework question bank of RTVU secondary school
- BUU-Real-[PHP]XXE
- 70000 words of detailed explanation of the whole process of pad openvino [CPU] - from environment configuration to model deployment
- QT releases multilingual International Translation
- left_ and_ right_ Net normal version
- Wechat applet +php realizes authorized login
- QT qtablewidget table column top requirements ideas and codes
- 实用的小工具指令
猜你喜欢
Webrtc quickly set up video call and video conference
体验碎周报第 102 期(2022.7.4)

Introduction to AMBA
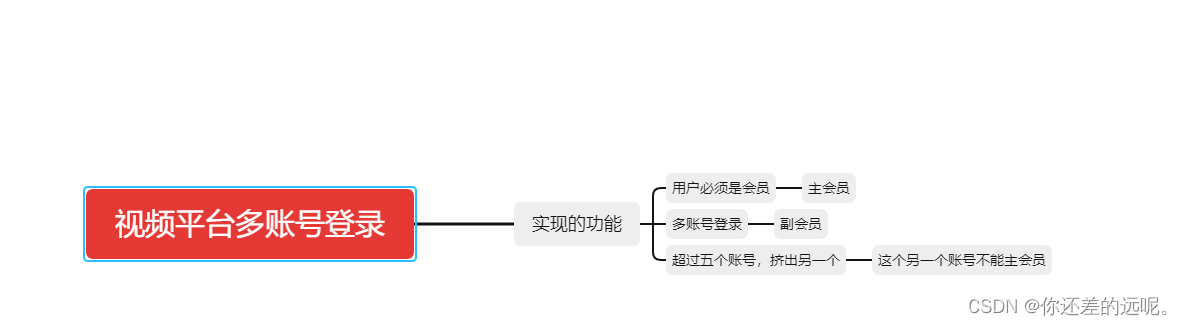
如何实现视频平台会员多账号登录

卸载Google Drive 硬盘-必须退出程序才能卸载

Impact relay jc-7/11/dc110v
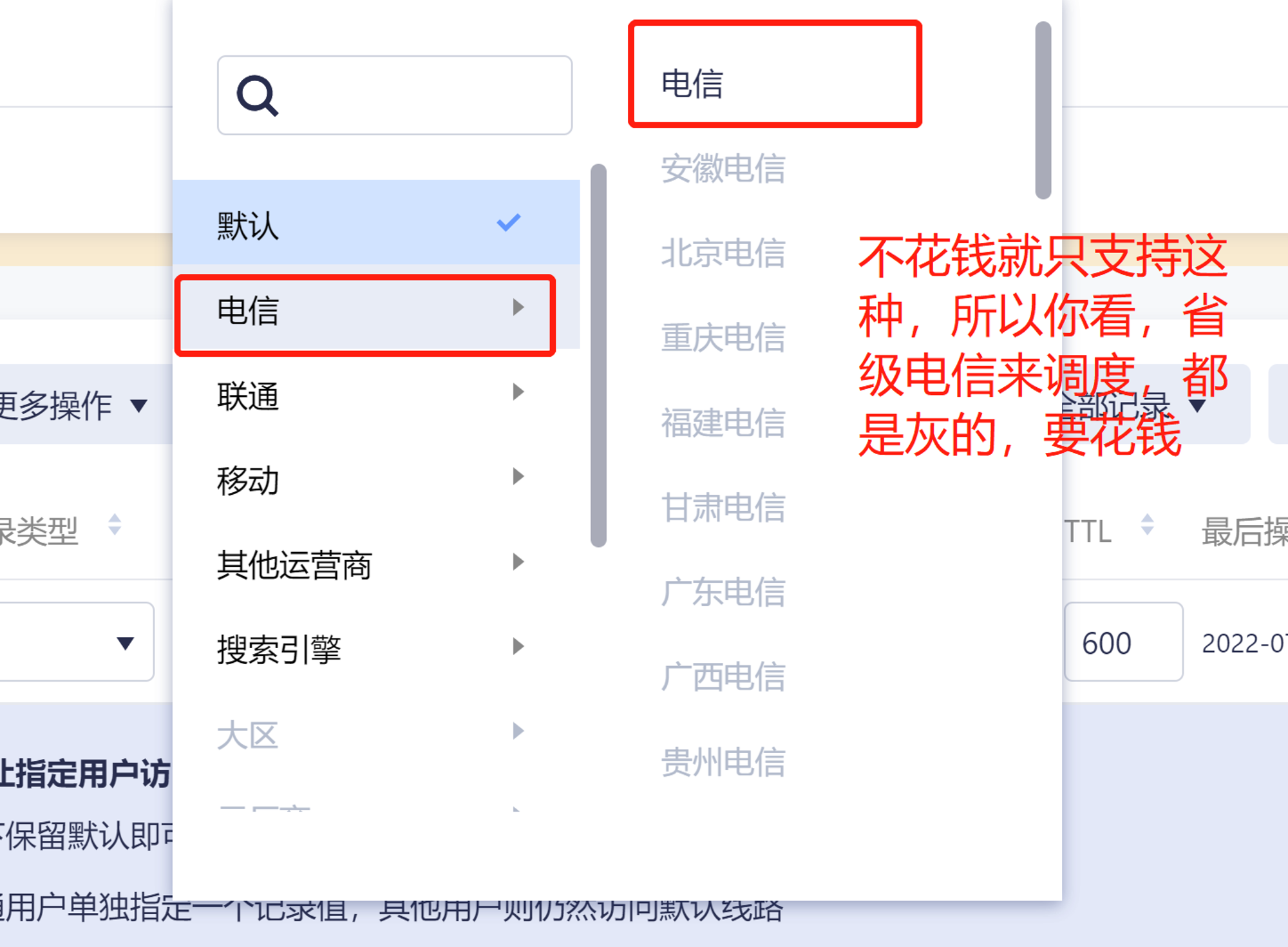
gslb(global server load balance)技术的一点理解

Take you to quickly learn how to use qsort and simulate qsort
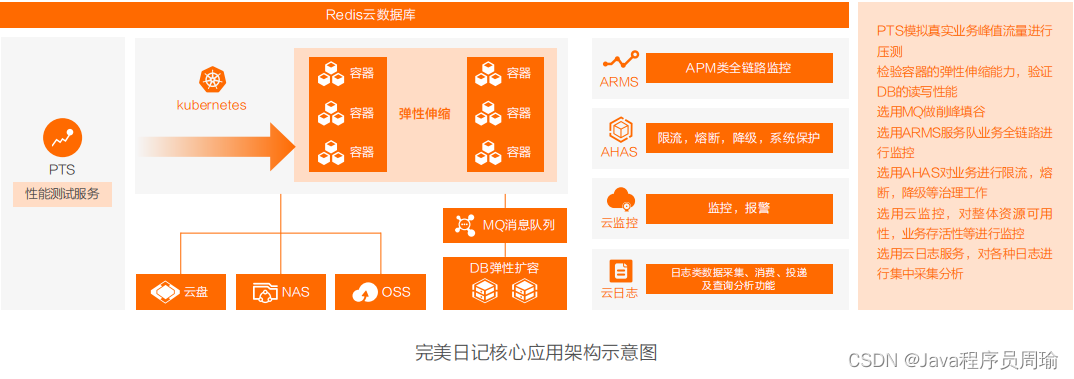
Actual cases and optimization solutions of cloud native architecture

Weekly summary (*63): about positive energy
随机推荐
el-select如何实现懒加载(带搜索功能)
Nexus 6p downgraded from 8.0 to 6.0+root
2022.7.2-----leetcode. eight hundred and seventy-one
Design and implementation of redis 7.0 multi part AOF
2022.7.2-----leetcode.871
Steady! Huawei micro certification Huawei cloud computing service practice is stable!
Programmers don't talk about morality, and use multithreading for Heisi's girlfriend
Yiwen unlocks Huawei's new cloud skills - the whole process of aiot development [device access - ESP end-to-side data collection [mqtt]- real time data analysis] (step-by-step screenshot is more detai
1480. Dynamic sum of one-dimensional array
【无标题】
Halcon图片标定,使得后续图片处理过后变成与模板图片一样
2022.7.3-----leetcode. five hundred and fifty-six
px em rem的区别
JS how to convert seconds into hours, minutes and seconds display
剑指 Offer II 038. 每日温度
Kubernets first meeting
fastjson
JS get the attribute values nested in the object
BUU-Crypto-[GUET-CTF2019]BabyRSA
How to clone objects