30 minutes to understand PCA principal component analysis

source ： Algorithm food house

This article shares with you PCA The concept of principal component analysis and in Python The use of . I also shared two articles before , It's also very good , It can be combined to see , Deepen the understanding .

Article to read PCA The mathematical principle of the algorithm

Let's talk about the dimensionality reduction algorithm ：PCA Principal component analysis

PCA Principal component analysis algorithm (Principal Components Analysis) It is one of the most commonly used dimensionality reduction algorithms . With low information loss ( Measured by the variance of distribution between samples ) Reduce the number of features .

PCA Algorithms can help Analyze the components with the greatest distribution difference in the sample ( The principal components ), Help data visualization ( Down to 2 Dimension or 3 After dimension, it can be visualized with scatter diagram ), Sometimes it can also play Reduce the noise in the sample The role of ( Part of the lost information is noise ).

One 、PCA Intuitive understanding of algorithms

Intuitively ,PCA Principal component analysis is similar to finding the direction long axis with the greatest difference in each position of a group of sample points in turn .

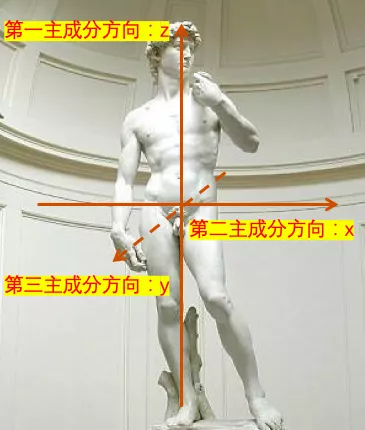
Suppose that all cells in a person are regarded as sample points one by one . These sample points can be used 3 Coordinates to represent , From left to right x Direction , From front to back y Direction , From bottom to top is z Direction .

So what is their first principal component ？ The long axis corresponding to the first principal component is along the direction from the foot to the head , That is, the usual up and down direction , namely z Direction . This direction is the main long axis . The position difference of these sample points is basically 70% The above comes from the difference in this direction .

What is their second principal component ？ The second principal component corresponds to the direction from left arm to right arm , That is, the usual left-right direction , namely y Direction . This direction is perpendicular to the long axis of the first principal component , The location differences of these sample points are about 20% Left and right come from the difference in this direction .

What is their third principal component ？ The third principal component direction is along the direction from the chest to the back , That is, the usual fore-and-aft direction , namely x Direction . This direction is perpendicular to the long axis of the first two principal components , The position difference of sample points is generally less than 10% The difference from this direction , Of course , Except for some students who are more rounded .

Now? , If you want to reduce the coordinates of these sample points to 2 One to indicate , And keep as much information about the location differences between sample points as possible , that , obviously , The coordinates of the first principal component and the second principal component should be retained .

Now? , Suppose this person is lying on a reclining chair , Now the first principal component of these sample points is obviously no longer from bottom to top z Direction . We should rotate our coordinate system , Give Way z The axis is in the same direction as the reclining chair , This new z The direction is the first principal component direction of these sample points . Similarly , You also need to rotate x Axis and y The axis obtains the new second principal component direction and the third principal component direction .

The process of rotating the old coordinate system to find the direction of the principal component is PCA Principal component analysis .

Two 、PCA Mathematical description of the algorithm

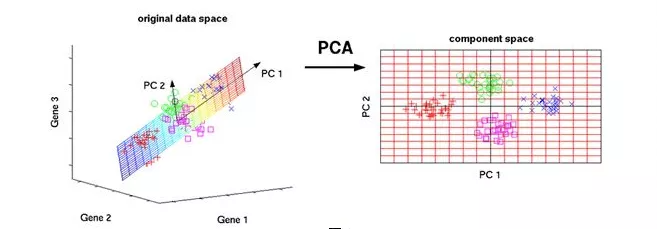
PCA Principal component analysis (Principal Components Analysis) It's a kind of passing Orthogonal linear combination The way , Maximize the variance between samples Of Dimension reduction Method .

From a geometric point of view ,PCA The principal component analysis method can be regarded as through Orthogonal transformation , Rotate and translate the coordinate system , The first several new coordinates with the largest variance of the projection coordinates of the sample points are retained .

Here are a few key words to explain :

• Dimension reduction ： Take the original sample m Victor requisitioned less k Features replace . Dimension reduction algorithm can be understood as a data compression method , It may lose some information .

• Orthogonal linear combination ：k A new feature is through m It is produced by linear combination of Gejiu features , also k The coefficient vector of a linear combination is the unit vector , And they are orthogonal to each other .

• Maximize the variance between samples ： The first 1 Principal component features maximize the characteristic variance between samples , The first 2 The three principal component features are satisfying the 1 Maximize the characteristic variance between samples under the orthogonal constraints of principal components ……

3、 ... and 、PCA Example of algorithm switching

In the following example, we call sklearn Medium PCA Dimension reduction algorithm interface , Dimensionality reduction of Boston house price data set (13 Dimension down to 7 dimension ).

import numpy as np
import pandas as pd

import matplotlib.pyplot as plt
from sklearn import datasets

boston = datasets.load_boston()
dfdata = pd.DataFrame(boston.data,columns = boston.feature_names)
dfdata.head()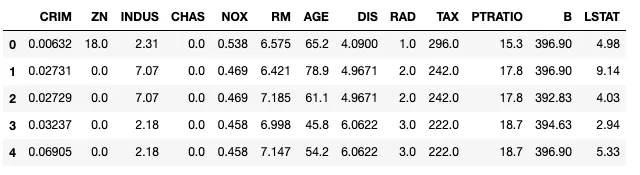

#  The value range of different features varies greatly , We first normalize the standard normal 
#  The normalized result is taken as  PCA Dimension reduction input 
from sklearn.preprocessing import StandardScaler
scaler = StandardScaler()
scaler.fit(dfdata.values)
X_input = scaler.transform(dfdata.values)

#  Our inputs are 506 Samples ,13 Whitman's sign 
print(X_input.shape)

(506, 13)

#  application PCA Carry out dimension reduction 

from sklearn.decomposition import PCA
pca = PCA(n_components=7)
pca.fit(X_input)
X_output = pca.transform(X_input)

#  After the dimension reduction , Only 7 Whitman's sign 
print(X_output.shape)

(506, 7)

#  Check the variance corresponding to each principal component and the proportion in the total variance 
#  You can see before 7 Principal components have explained the distribution of samples 90% The difference .

print("explained_variance:")
print(pca.explained_variance_)

print("explained_variance_ratio:")
print(pca.explained_variance_ratio_)

print("total explained variance ratio of first 7 principal components:")
print(sum(pca.explained_variance_ratio_)

explained_variance:
[6.1389812  1.43611329 1.2450773  0.85927328 0.83646904 0.65870897
 0.5364162 ]
explained_variance_ratio:
[0.47129606 0.11025193 0.0955859  0.06596732 0.06421661 0.05056978
 0.04118124]
total explained variance ratio of first 7 principal components:
0.8990688406240493

# Visualize the variance of each principal component contribution 
%matplotlib inline
%config InlineBackend.figure_format = 'svg'

import matplotlib.pyplot as plt
plt.figure()
plt.plot(np.arange(1,8),pca.explained_variance_,linewidth=2)
plt.xlabel('components_n', fontsize=16)
plt.ylabel('explained_variance_', fontsize=16)
plt.show()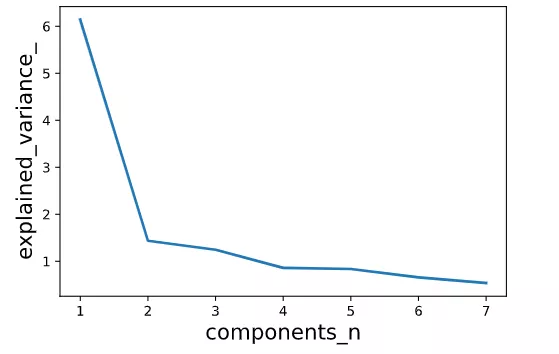

#  Check the orthogonal transformation matrix corresponding to the dimension reduction , That is, each projection vector 
W = pca.components_
#  Verify orthogonality 
np.round(np.dot(W,np.transpose(W)),6)

array([[ 1.,  0., -0., -0., -0.,  0., -0.],
       [ 0.,  1., -0.,  0.,  0., -0., -0.],
       [-0., -0.,  1.,  0., -0.,  0., -0.],
       [-0.,  0.,  0.,  1., -0., -0.,  0.],
       [-0.,  0., -0., -0.,  1.,  0.,  0.],
       [ 0., -0.,  0., -0.,  0.,  1., -0.],
       [-0., -0., -0.,  0.,  0., -0.,  1.]])

#  Visualize the first two dimensions of the reduced dimension data 

%matplotlib inline
%config InlineBackend.figure_format = 'svg'

plt.scatter(X_output[:,0],X_output[:,1])
plt.xlabel("components_1")
plt.ylabel("components_2")
plt.show()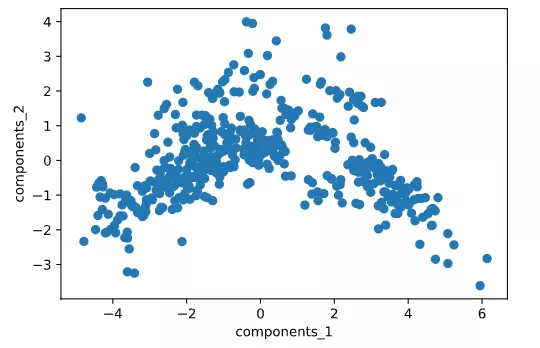

Four 、PCA The mathematical principle of the algorithm

High number reminder ahead .

Underneath PCA Deduction of mathematical principle of Algorithm , Certificate No k The principal component projection vector is exactly the... Of the covariance matrix of the sample k Eigenvectors corresponding to large eigenvalues .

The following deduction will use some knowledge of linear algebra and calculus in Advanced Mathematics .

Students without relevant mathematical foundation can skip , In practice, just master PCA Intuitive concept of the algorithm and how to use it , Basically enough .

Suppose that the characteristics of the sample are represented by a matrix , Each line represents a sample , Each column represents a feature .

Assuming that Dimensional , I.e. samples , Whitman's sign .

Now look for the first principal component .

Suppose the first principal component projection vector is , It is a unit column vector , Dimension is ,

Then the coordinate after projection is

The coordinate variance between the projected samples can be expressed as

Bars mean averaging the samples , Because it has nothing to do with the sample , It can be reduced to :

be aware It happens to be The covariance matrix of .

Next we want to maximize the coordinate variance , At the same time, the unit length constraint must be satisfied :

For extreme value conditions with constraints , We can apply Lagrange multiplier method in calculus . Construct the following Lagrange function .

402 Payment Required

The subscript representation can be used to prove , For quadratic form , There is the following vector derivation formula ：

We can deduce that ：

402 Payment Required

It can be seen that , Is the eigenvalue of the covariance matrix , Is the corresponding eigenvector . Because the covariance matrix is a real symmetric matrix , Its characteristic value must be greater than or equal to 0.

meanwhile , The coordinate variance between the projected samples can be expressed as ：

402 Payment Required

To maximize the coordinate variance between samples , The largest eigenvalue of the covariance matrix should be taken , Then it should be the eigenvector corresponding to the maximum eigenvalue of the covariance matrix .

Similarly , It can be proved that k The first principal component projection vector is the... Of the covariance matrix k Eigenvectors corresponding to large eigenvalues .

Because the eigenvectors of different eigenvalues of the matrix are orthogonal to each other , Therefore, these projection vectors satisfy the orthogonal condition .