Link list of high frequency written interview question brushing summary (distribution explanation & code annotation)

JZ22  Last in the list k Nodes 【 Simple 】

Topic

  Ideas

• Double pointer , Define two pointers ：first and second
• The previous pointer goes first k Step , Before it goes k In step , If a pointer is found first empty , Then return to nullptr;
• As shown in the figure below , Next, the two pointers move forward at the same time , When first When you come to the end and leave the space empty ,second Just walk to the k A place

Complexity analysis

• Time complexity ： O(n)
• Spatial complexity ： O(1)

Code

class Solution {
public:
        ListNode* FindKthToTail(ListNode* pHead, int k) {
        if(pHead==nullptr)  return nullptr; 
        // Define double pointer 
        ListNode* first = pHead;
        ListNode* second = pHead;
        // The first pointer goes first k Step 
        while(k > 0) {
            // If the length of the linked list is less than k, Returns a length of 0 The linked list of 
            if(first==nullptr)  return nullptr; 
            first = first->next;
            k--;
        }
        // Both hands go forward at the same time , When the current pointer is set to null , The last pointer reaches 
        while(first!=nullptr) {
            first = first->next;
            second = second->next;
        }
        return second;
    }
};

---

JZ18  Delete the node of the linked list 【 Simple 】

Topic

Ideas

• We need to pay attention to Is the list empty   and Only one header node cannot be deleted The situation of
• Define two pointers pre and cur, When cur When pointing to the node to be deleted , change pre To delete the node （ It is equivalent to crossing that node ）

Complexity analysis

• Time complexity ： O(n)
• Spatial complexity ： O(1)

Code

class Solution {
public:
    ListNode* deleteNode(ListNode* head, int val) {
        auto pre = head, cur = head; //cur Point to the node to delete ,pre Point to its precursor node 
        if(head->val == val)  return head->next; // There is only one header node 
        while(cur->val != val) { // Find the node to be deleted 
            pre = cur;
            cur = cur->next;
        }
        pre->next = cur->next; // Change the precursor node pre The direction of 
        return head;
    }
};

---

JZ76  Delete duplicate nodes in the list 【 More difficult 】

Topic

Ideas

Speed pointer

1. Define two pointers （slow、fast）, And virtual nodes dummy, Initialize the three pointers ,slow and fast adjacent ;
2. When encountering repetition ,「 Only fast The pointer 」 Move forward , here slow and fast Not adjacent ;
3. If not repeated , be slow Pointers and fast The pointer moves one step forward ;

「 When repetition occurs ,slow Pointers and fast The pointer must not be adjacent , At this point, updating the location of both can achieve the effect of deletion 」

The process is as follows ：

Complexity analysis

Time complexity ：O(N), This method needs to traverse the entire linked list

Spatial complexity ：O(1), Except for some pointers , No extra space is used

Code

class Solution {
public:
    ListNode* deleteDuplication(ListNode* pHead) {
        if(!pHead)    return NULL;
        ListNode* slow = new ListNode(-1), *fast = new ListNode(-1), *dummy = new ListNode(-1); 
        dummy->next = pHead; 
        //  Initialize two pointers 
        slow = dummy;    fast = dummy->next; 
        while(fast) {
            //  Duplicate encountered 
            while(fast->next && fast->val == fast->next->val) {
                fast = fast->next; 
            }
            //  Duplicate encountered 
            if(slow->next != fast) {
                slow->next = fast->next; 
                fast = slow->next; 
            } 
            //  No repetition 
            else { 
                fast = fast->next; 
                slow = slow->next; 
            }
        }
        return dummy->next;
    }
};

---

JZ35  Replication of complex linked list 【 More difficult 】

Topic

Code

class Solution{
public:
    RandomListNode* Clone(RandomListNode* pHead) {
        if(!pHead) return nullptr;
        RandomListNode* cur = pHead;
        unordered_map<RandomListNode*, RandomListNode*> map;
        // Copy each node , And establish  “ Original node  ->  New node ”  Of  Map  mapping 
        while(cur != nullptr) {
            map[cur] = new RandomListNode(cur->label);
            cur = cur->next;
        }
        cur = pHead;
        // To build a new linked list  next  and  random  Point to 
        while(cur != nullptr) {
            map[cur]->next = map[cur->next];
            map[cur]->random = map[cur->random];
            cur = cur->next;
        }
        // Return the head node of the new linked list 
        return map[pHead];
    }
};

---

Merge two ordered lists 【 Simple 】

Topic

Ideas

• The most direct way of thinking is —— recursive ：
• As long as one linked list is empty , Just return to another linked list , No consolidation is required ;
• Otherwise, see which header node of the two linked lists is smaller , The smaller head node points to the... Of the remaining nodes merge result .
• Merge all nodes of the two linked lists recursively .

Complexity analysis

• Time complexity ：O(n+m), Recursion is removed every time it is called  l1  perhaps  l2  The head node of （ Until at least one linked list is empty ）, function mergeTwoLists  Each node will be called recursively at most once .
• Spatial complexity ：O(n+m), Recursively call mergeTwoLists It consumes stack space , The size of the stack space depends on the depth of the recursive call . End recursive call ,mergeTwoLists The function can call at most n+m Time .

Code

class Solution{
public:
    ListNode* mergeTwoLists(ListNode* l1, ListNode* l2){
        if(l1==nullptr) return l2;                  // l1 Is an empty list , return l2 Linked list 
        else if(l2==nullptr) return l1;             // l2 Is an empty list , return l1 Linked list 
        else if(l1->val < l2->val) {
            l1->next = mergeTwoLists(l1->next, l2); // l1 The value of the header node is small , Points to the remaining nodes merge result 
            return l1;                              //  Return to the merged l1 Linked list 
        }
        else {
            l2->next = mergeTwoLists(l2->next, l1); // l2 The value of the header node is small , Points to the remaining nodes merge result 
            return l2;                              //  Return to the merged l2 Linked list 
        }
    }
};

Optimize

• use iteration Instead of recursion , The space complexity is optimized to O(1).
• When l1 and l2 Are non empty linked lists , Determine which head node of the linked list has a smaller value , Add smaller nodes to the result , When a node is added to the result , Move the node in the corresponding list back one bit .
• First , Set a sentinel node prehead , Make it easier to return the merged linked list . Maintain a prev The pointer , The point is to adjust its next The pointer . If l1 The value of the current node is less than or equal to l2 , We will take l1 The current node is connected to prev The nodes will be followed by l1 Move the pointer back one bit . otherwise , We are right. l2 Do the same thing . No matter which element we put next , We all need to put prev Move backward one bit . until l1 perhaps l2 Yes null.
• At the end of the cycle , l1 and l2 At most one is not empty . Because the two linked lists are in order , So no matter which list is not empty , It contains all the elements larger than all the elements in the previously merged linked list . Simply connect the non empty linked list to the merged linked list , And return to the merge list .

class Solution {
public:
    ListNode* mergeTwoLists(ListNode* l1, ListNode* l2) {
        ListNode* preHead = new ListNode(-1);
        ListNode* prev = preHead;
        while (l1 != nullptr && l2 != nullptr) {
            if (l1->val < l2->val) {
                prev->next = l1;
                l1 = l1->next;
            } 
            else {
                prev->next = l2;
                l2 = l2->next;
            }
            prev = prev->next;
        }
        //  After the merger , At most one linked list has not been merged , Directly point the end of the linked list to the unfinished linked list 
        prev->next = l1 == nullptr ? l2 : l1;
        return preHead->next;
    }
};

---

Intersecting list & JZ52  The first common node of two linked lists 【 Simple 】

Topic

Ideas

The basic idea is Hash Collection stores linked list nodes ： Traverse the list first A, And add each node to the hash set ; Then traverse B, Traverse to each node , Determine whether the node is in the hash set . Until I find B In the A The nodes in the , And start from this node , All nodes are coincident , This point is what we are looking for .

Double pointer Reduce space complexity to O(1)

The specific methods are as follows :

Give an example , Create an ideal situation ： When the length of two linked lists is equal , You can use double pointers to solve the problem

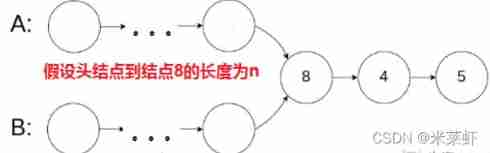
• initialization ： The pointer ta Point to the list A Head node of , The pointer tb Point to the list B Head node of
• if ta==tb, It indicates that the first public node has been reached ;
• otherwise （ta != tb）, The two pointers move back one unit together （ta++;tb++）

that , How to make two linked lists equal in length ？

Suppose the linked list A The length is a, Linked list B The length is b, obviously a!=b, however a+b==b+a

therefore , It can make a+b As A New length , Give Way b+a As B New length

here , Same length , You can use the double pointer algorithm  

Two categories: “ Double pointer ” Algorithm analysis 【 Detailed explanation with examples +AC Code 】_ Xia Xu's blog -CSDN Blog First , Introduce the double pointer algorithm . When we use simple algorithms to solve problems violently , By mining certain properties , The complexity of the algorithm is reduced from O(n^2)->O(n) , We call the algorithm with this property double pointer algorithm 【 In fact, the double pointer algorithm is very extensive , It is not just used to maintain two windows , But here, , We narrowed it down 】. Two commonly used types of double pointer algorithms ： One is ： Two pointers point to two sequences respectively ( “ Merge sort ” This kind of pointer is used , Specific operation ： Move two pointers at a time , When the two pointers have finished moving , The sorting process ends ); The other is ： Two pointers point to the same sequence , One points to the beginning , One points to the end ( Like fast platoon ).https://blog.csdn.net/Luoxiaobaia/article/details/106182893

Complexity analysis

• Time complexity ： Both hash and double pointer algorithms are O(n+m), In the worst case , The public node is the last , Need to traverse m+n Nodes
• Spatial complexity ： The hash is O(m), Hash sets store linked lists A All nodes in ; The double pointer algorithm optimizes the space complexity to O(1).

Code

//  Double pointer algorithm 
class Solution {
public:
    ListNode* FindFirstCommonNode(ListNode* pHead1, ListNode* pHead2) {
        ListNode* ta=pHead1, *tb=pHead2; // Define two pointers to the head nodes of two linked lists 
        while(ta!=tb) { // When two pointers are not in the same position , That is, when the public node is not reached 
            // When the public node is not reached , Keep pointing to the linked list 1 The next node of , To the end and then point to 2 Of （ Ensure equal length ）
            ta = ta ? ta->next : pHead2;
            // When the public node is not reached , Keep pointing to the linked list 2 The next node of , To the end and then point to 1 Of （ Ensure equal length ）
            tb = tb ? tb->next : pHead1;
        }
        return ta; // Return the first public node as required 
    }
};

---

Circular list 【 Simple 】

Topic

Advanced ： You can use  O(1)（ namely , Constant ） Does memory solve this problem ？ 

Ideas

The simplest way to think about it is ： Traverse all nodes , Judge whether the node has been accessed before . Specific use Hashtable Store the accessed nodes , If arriving node already exists in hash table , It means that the linked list is circular , Otherwise, join the node , Until the whole list is traversed .

Complexity analysis

• Time complexity ：O(N),N  Indicates the number of nodes in the linked list . In the worst case, each node should be traversed once .
• Spatial complexity ：O(N),N  Indicates the number of nodes in the linked list . Mainly for the cost of hash table , In the worst case, insert each node into the hash table once .

Code

//  Hashtable 
class Solution{
public:
    bool hasCycle(ListNode *head) {
        unordered_set<ListNode*> seen;        //  Create hash table 
        while(head != nullptr) {              //  When the linked list is not traversed 
            if(seen.count(head)) return true; //  If a node appears repeatedly , Description is a circular linked list , return true
            seen.insert(head);                //  If only for the first time , Save to hash table 
            head = head->next;                //  Point to next node 
        }
        return false;                         //  Not a circular return false
    }
};

Advanced algorithm _ Speed pointer

Use O(1) Memory solution , You use Speed pointer .

Speaking of the speed pointer , We need to be right Floyd Judge circle （ Tortoise and the hare ） Algorithm Know something about .

Suppose a rabbit and a tortoise move on the same list and the rabbit runs faster than the tortoise , If there is no ring , Then the rabbit will always be in front of the tortoise ; If there is a ring , Then the rabbit will enter the ring first , Then keep running in the loop , In this way, the tortoise will always go into the ring and cycle , It is possible to meet .

Define two pointers （ Fast and slow ） To simulate rabbits and turtles , Slow pointer moves one step at a time , Fast pointer moves two steps at a time . We set the fast pointer to a position in front of the slow pointer （ The slow pointer is head Location , Come on, where's the pointer head.next Location ）, This can better explain whether the slow pointer can catch up with the fast pointer （ If the fast pointer to the end of the list is not caught up , It means there is no ring ）; It can also guarantee the following code while Be able to cycle （ If it is do-while In words , The initial position of the fast and slow pointers can be the same ）.

Speed pointer code

//  Speed pointer 
class Solution {
public:
    bool hasCycle(ListNode* head) {
        if(head==nullptr || head->next==nullptr) 
            return false;
        ListNode* slow = head;
        ListNode* fast = head->next;
        while(slow != fast) {
            if(fast==nullptr || fast->next==nullptr) 
                return false;
            slow = slow->next;
            fast = fast->next->next;
        }
        return true;
    }
};

Complexity analysis after optimization

• Time complexity ：O(N), among N  Is the number of nodes in the linked list . When there is no ring in the linked list , The fast pointer will reach the end of the linked list before the slow pointer , Each node in the linked list can be accessed at most twice ; When there are links in the linked list , After each round of movement , The distance between the fast and slow pointers will be reduced by one . The initial distance is the length of the ring , So move at most N  round .
• Spatial complexity ：O(1), The extra space of only two pointers is used .

---

Reverse a linked list 【 Simple 】

Topic

Ideas

• With the help of Double pointer Continuously realize local inversion
• First define two pointers ,pre->head,cur->null,pre stay cur front .
• When pre->next=cur when , This completes the local reversal of the points of the nodes at the corresponding positions of the current two pointers .
• Then the two pointers keep moving forward until the entire linked list is traversed .
• The picture below is Part of the process of moving two pointers   and Schematic diagram of local inversion

Complexity analysis

• Time complexity ：O(N)
• Spatial complexity ：O(1), Extra space using two pointers

Code

class Solution{
public:
    ListNode* reverseList(ListNode* head) {
        ListNode* cur = nullptr, *pre = head;
        while(pre != nullptr) {
            ListNode* temp = pre->next; // Record the location of the next node 
            pre->next = cur;            // Local inversion 
            cur = pre;                  //cur Move one unit forward 
            pre = temp;                 //pre Move one unit forward 
        }
        return cur;                     // Return the inverted linked list 
    }
};

---

Addition of two numbers 【 Simple 】

Question surface and 2 A train of thought explains in detail

Introduction and use of hash algorithm 【 Power button -HOT-100 And “ Sum of two numbers ”】_ Xia Xu's blog -CSDN Blog 1. Sum of two numbers 【 difficulty 】 Simple table of contents ： Answer key ： Ideas 1： Code 1： Ideas 2： Code 2： Some introduction of hash algorithm ： Illustrates the use of hash tables ： Topic ： Given an array of integers nums And an integer target value target, Please find the sum in the array as the target value target The two integers of , And return their array subscripts . You can assume that each input corresponds to only one answer . however , The same element in the array cannot be repeated in the answer . You can return the answers in any order . Example 1： Input ：nums = [2,7,11,15], target ...https://blog.csdn.net/Luoxiaobaia/article/details/121214481

Code 1&2

class Solution {
public:
    vector<int> twoSum(vector<int>& nums, int target) {
        int n = nums.size();
        for (int i=0; i<n; ++i) {
            for (int j=i+1; j<n; ++j) {
                if (nums[i] + nums[j] == target) {
                    return {i, j};
                }
            }
        }
        return {};
    }
};

class Solution {
public:
    vector<int> twoSum(vector<int>& nums, int target) {
        unordered_map<int, int> hashtable;
        for (int i=0; i<nums.size(); ++i) {
            auto it = hashtable.find(target - nums[i]);
            if (it != hashtable.end()) {
                return {it->second, i};
            }
            hashtable[nums[i]] = i;
        }
        return {};
    }
};

---

Circular list 2【 secondary 】& JZ23  The entry node of a link in a list

Topic

  

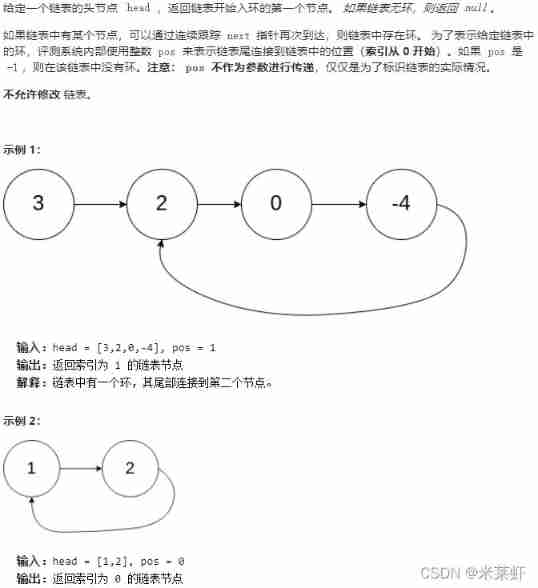
Ideas

The simplest way to think about it is ： Traverse all nodes , Judge whether the node has been accessed before . Specific use Hashtable Store the accessed nodes , If arriving node already exists in hash table , It means that the linked list is circular , Otherwise, join the node , Until the whole list is traversed .

Complexity analysis

• Time complexity ：O(N),N  Indicates the number of nodes in the linked list . In the worst case, each node should be traversed once .
• Spatial complexity ：O(N),N  Indicates the number of nodes in the linked list . Mainly for the cost of hash table , In the worst case, insert each node into the hash table once .

Code

class Solution {
public:
    ListNode *detectCycle(ListNode *head) 
    {
        unordered_set<ListNode *> visited;
        while (head != nullptr) {
            if (visited.count(head))    return head;
            visited.insert(head);
            head = head->next;
        }
        return nullptr;
    }
};

Advanced _ Speed pointer

Space complexity is optimized to O(1)

class Solution {
public:
    ListNode *detectCycle(ListNode *head) {
        ListNode *slow = head, *fast = head;
        while (fast != nullptr) {
            slow = slow->next;
            if (fast->next == nullptr) 
                return nullptr;
            fast = fast->next->next;
            if (fast == slow) {
                ListNode *ptr = head;
                while (ptr != slow) {
                    ptr = ptr->next;
                    slow = slow->next;
                }
                return ptr;
            }
        }
        return nullptr;
    }
};

---

Rearrange the list 【 secondary 】

Topic

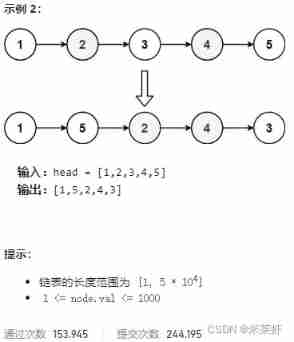
Ideas

1. Divide the linked list into the first half and the second half . Use the speed pointer to find the midpoint （ Point of division ）, It is located in n/2 The point of . It can be used Speed pointer Find this point . At the same time, this point is also the last point of the list after rearrangement , So it's going to be next Null pointer .
2. Flip the second half of the linked list from the midpoint .
3. Insert the second half of the linked list into the first half of the linked list according to the rule of one node apart .

Complexity analysis

• Time complexity ：O(N)
• Spatial complexity ：O(1), Extra space using two pointers

Code

class Solution {
public:
    void reorderList(ListNode* head) {
        //  If the linked list has only three nodes, there is no need to rearrange （ There was no difference after rearrangement ）
        if(!head || !head->next || !head->next->next)  return; 

        //  Use the speed pointer to find the midpoint s
        auto s=head, f=head;           // Define speed pointer 
        while(f && f->next) {          // Until the fast pointer goes to the end    
            s = s->next;               // The slow pointer moves one unit at a time 
            f = f->next->next;         // The fast pointer moves two units at a time 
        }
       
        auto pre = s, cur = s->next;   // Record the midpoint and the next node in advance （ The head node of the second half ）
        s->next = nullptr;             // Place the midpoint s（ That is, the last node of the list after rearrangement ） Of next empty 
       
        //  Reverse the second half of linked list , combination  “ Double pointer to achieve reverse linked list ”  understand 
        while(cur) {
            auto o = cur->next;
            cur->next = pre;
            pre = cur;
            cur = o;
        }
       
        // Combine the front and back linked lists according to the rules （ Merge list ）
        auto p = head, q = pre;
        while (q->next) {
            auto o = q->next;
            q->next = p->next;
            p->next = q;
            p = q->next;
            q = o;
        }
    }
};

---

Binary search tree and double linked list 【 secondary 】

Topic

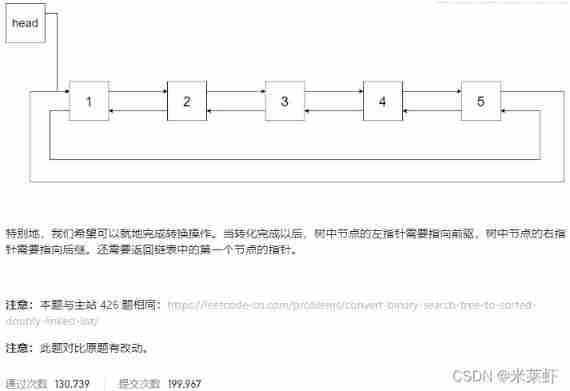
Ideas

< This topic draws lessons from   When the forest is deep, see the deer L6

First, let's introduce the binary search tree ：

Binary search tree is an ordered binary tree , So we can also call it binary sort tree .

A binary tree with the following properties is called a binary search tree ： If its left subtree is not empty , Then all values on the left subtree are less than its root node ; If its right subtree is not empty , Then all values on the right subtree are greater than its root node . Its left subtree and right subtree are also binary search trees .

The middle order traversal of binary search tree is ： Left => root => Right ; The middle order traversal of binary search tree is orderly from small to large .

As shown in the figure below , This question requires us to put a tree Binary search tree become Sorted circular bidirectional linked list

The middle order traversal of binary search tree is ordered , Therefore, this problem is changed on the basis of medium order recursive traversal .

The specific process is as follows ：

1、 We define two pointers pre and head,pre The pointer is used to save the previous node traversed in the middle order ,head The pointer is used to record the header node of the sorting linked list .

2、 Middle order ergodic binary tree , Because it's a middle order traversal , So the traversal order is the establishment order of the double linked list . We just need to go through the middle order traversal , Modify the left and right pointers of each node , Connect scattered nodes into a two-way circular linked list .

3、 First, traverse the left subtree of the binary tree , Then the current root node root.

• Current drive node pre Isn't empty , Add precursor node pre The right pointer to the current root node root, namely pre->right = root.
• Current drive node pre It's empty time ： Represents accessing the chain header node , Write it down as  head = root , Save the header node .

4、 every last root When a node accesses, its left subtree must have been accessed , So rest assured to modify its left The pointer , take root Of left The pointer points to its predecessor node , namely root->left = pre, In this way, the two-way pointer between the two nodes can be modified .

5、 Then the precursor node pre Move right to the current root node , Next, recurse to the right subtree and repeat the above operation .

6、 Complete the above steps , It just turns the binary tree into a two-way sorted linked list , We also need to connect the beginning and end of the linked list , Turn it into a two-way circular sort linked list .

Do the following ：
head->left = pre;
pre->right = head;

Complexity

n Is the number of nodes in the binary tree , Middle order traversal requires access to all nodes , So the time complexity is zero O(n)

Code

class Solution {
public:
    Node* pre = nullptr, *head = nullptr;
    Node* treeToDoublyList(Node* root) {
        if (!root) return root;
        dfs(root);
        head->left = pre;
        pre->right = head;
        return head;
    }
    void dfs(Node* root){
        if (!root) return;//  Recursive boundary :  The leaf node returns 
        dfs(root->left);  // The left subtree 
        if (pre) pre->right = root;
        else head = root; //  Save the chain header node 
        root->left = pre; 
        pre = root;
        dfs(root->right); // Right subtree 
    }
};