PI control of grid connected inverter (grid connected mode)

1. Inverter topology and mathematical model

The following figure shows the basic structure model of the inverter .

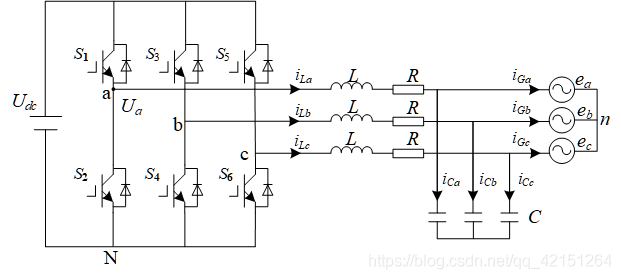
According to the model, write the mathematical model of the inverter as follows ：
$$\{\begin{array}{l}{U}_a-L\frac{d{i}_a}{dt}-i_{a}R-e_a=0\\ U_b-L\frac{d{i}_b}{dt}-i_{b}R-e_b=0\\ U_c-L\frac{d{i}_c}{dt}-i_{c}R-e_c=0\end{array}$$

2. Common transformations

2.1 abc-$\alpha \beta$ Transformation and its inverse transformation

The specific principle is not deduced here , Please refer to other materials .

$$\left[\begin{array}{c}{U}_{\alpha }\\ U_{\beta }\end{array}\right]=m\times \left[\begin{array}{ccc}1& -\frac{1}{2}& -\frac{1}{2}\\ 0& \frac{\sqrt{3}}{2}& -\frac{\sqrt{3}}{2}\end{array}\right]\left[\begin{array}{c}{U}_a\\ U_b\\ U_c\end{array}\right]$$

m The value of is related to the system requirements ;

$$\{\begin{array}{ll}m=\sqrt{\frac{2}{3}}& workratephaseetc.changein\\ m=\frac{2}{3}& picturevaluephaseetc.changein\end{array}$$

In control , We often choose amplitude invariant algorithm for control .

When $m=\frac{2}{3}$ Correspondingly, there is inverse transformation :

$$\left[\begin{array}{c}{U}_a\\ U_b\\ U_c\end{array}\right]=m\times \left[\begin{array}{cc}1& 0\\ -\frac{1}{2}& \frac{\sqrt{3}}{2}\\ -\frac{1}{2}& -\frac{\sqrt{3}}{2}\end{array}\right]\left[\begin{array}{c}{U}_{\alpha }\\ U_{\beta }\end{array}\right]$$

2.2 $\alpha \beta$-dq Axis transformation

$$\left[\begin{array}{c}{U}_d\\ U_q\end{array}\right]=\left[\begin{array}{cc}cos\phi & sin\phi \\ -sin\phi & cos\phi \end{array}\right]\left[\begin{array}{c}{U}_{\alpha }\\ U_{\beta }\end{array}\right]$$

The corresponding inverse transformation is
$$\left[\begin{array}{c}{U}_{\alpha }\\ U_{\beta }\end{array}\right]=\left[\begin{array}{cc}cos\phi & -sin\phi \\ sin\phi & cos\phi \end{array}\right]\left[\begin{array}{c}{U}_d\\ U_q\end{array}\right]$$
Here we need to pay attention to ：

1. In a general way , In the control of the inverter, the grid voltage is oriented to d Axis , Therefore, the angle in the transformation formula is the phase angle of the power grid .

2. according to dq And $\alpha \beta$ The equal positions of the coordinate axes are different , There are different forms of transformation , Specific reference to . Like European electric four dq Transformation

2.3 abc-dq Transformation

$$\left[\begin{array}{c}{U}_d\\ U_q\end{array}\right]=\frac{2}{3}\left[\begin{array}{ccc}cos\phi & cos(\phi -\frac{2}{3}\pi )& cos(\phi +\frac{2}{3}\pi )\\ -sin\phi & -sin(\phi -\frac{2}{3}\pi )& -sin(\phi +\frac{2}{3}\pi )\end{array}\right]\left[\begin{array}{c}{U}_a\\ U_b\\ U_c\end{array}\right]$$

3.dq Equation of parallel inverter in coordinate system

Will type （1） Conduct dq Change can get ：

$$\left[\begin{array}{c}{U}_d\\ U_q\end{array}\right]=L\frac{d}{dt}\left[\begin{array}{c}{i}_a\\ i_b\\ i_c\end{array}\right]\times T_{abc\_dq}+\left[\begin{array}{c}{i}_d\\ i_q\end{array}\right]R+\left[\begin{array}{c}{e}_d\\ e_q\end{array}\right]$$
among ：
$$\frac{d\left[\begin{array}{c}{i}_a\\ i_b\\ i_c\end{array}\right]\times T_{abc\_dq}}{dt}=\frac{d\left[\begin{array}{c}{i}_a\\ i_b\\ i_c\end{array}\right]}{dt}\times T_{abc\_dq}+\frac{d{T}_{abc\_dq}}{dt}\times \left[\begin{array}{c}{i}_a\\ i_b\\ i_c\end{array}\right]$$
among $\phi =\omega t$
$$\frac{d{T}_{abc\_dq}}{dt}=\omega \left[\begin{array}{ccc}-sin\phi & -sin(\phi -\frac{2}{3}\pi )& -sin(\phi +\frac{2}{3}\pi )\\ -cos\phi & -cos(\phi -\frac{2}{3}\pi )& -cos(\phi +\frac{2}{3}\pi )\end{array}\right]$$
therefore ：
$$\frac{d{T}_{abc\_dq}}{dt}\times \left[\begin{array}{c}{i}_a\\ i_b\\ i_c\end{array}\right]=\omega \times \left[\begin{array}{c}{i}_q\\ -i_d\end{array}\right]$$
Substitute into the original formula to get ：

$$\frac{d\left[\begin{array}{c}{i}_a\\ i_b\\ i_c\end{array}\right]}{dt}\times T_{abc\_dq}=\frac{d\left[\begin{array}{c}{i}_d\\ i_q\end{array}\right]}{dt}-\omega \times \left[\begin{array}{c}{i}_q\\ -i_d\end{array}\right]$$

Then the mathematical model of the grid connected inverter is ：
$$\left[\begin{array}{c}{U}_d\\ U_q\end{array}\right]=L\frac{d}{dt}\left[\begin{array}{c}{i}_d\\ i_q\end{array}\right]-\omega L\times \left[\begin{array}{c}{i}_q\\ -i_d\end{array}\right]+\left[\begin{array}{c}{i}_d\\ i_q\end{array}\right]R+\left[\begin{array}{c}{e}_d\\ e_q\end{array}\right]$$
namely ：
$$\{\begin{array}{c}{U}_d=L\frac{d{i}_d}{dt}-\omega L{i}_q+R{i}_d+e_d\\ U_q=L\frac{d{i}_q}{dt}+\omega L{i}_d+R{i}_q+e_q\end{array}$$
Laplace transform can get ：
$$\{\begin{array}{c}{U}_d=(Ls+R)i_d-\omega L{i}_q+e_d\\ U_q=(Ls+R)i_q+\omega L{i}_d+e_q\end{array}$$

4. Closed loop control

   According to the inverter model , The input to be built is Id* Output is Ud Of PI Control link . Decoupling control of inverter can be realized .（ First modification ： Decoupling is actually introduced here to eliminate the influence of disturbance on the system , such as Grid voltage 、 Current feedforward wait , After elimination, the system will become simple to pass PI Link to correct the system .）
introduce PI Links are available ：
$$\{\begin{array}{c}{U}_d=(Kp+\frac{Ki}{s})(i_d^{\ast }-i_d)-\omega L{i}_q+e_d\\ U_q=(Kp+\frac{Ki}{s})(i_q^{\ast }-i_q)+\omega L{i}_d+e_q\end{array}$$
   The following figure shows the overall control block diagram of the inverter system ：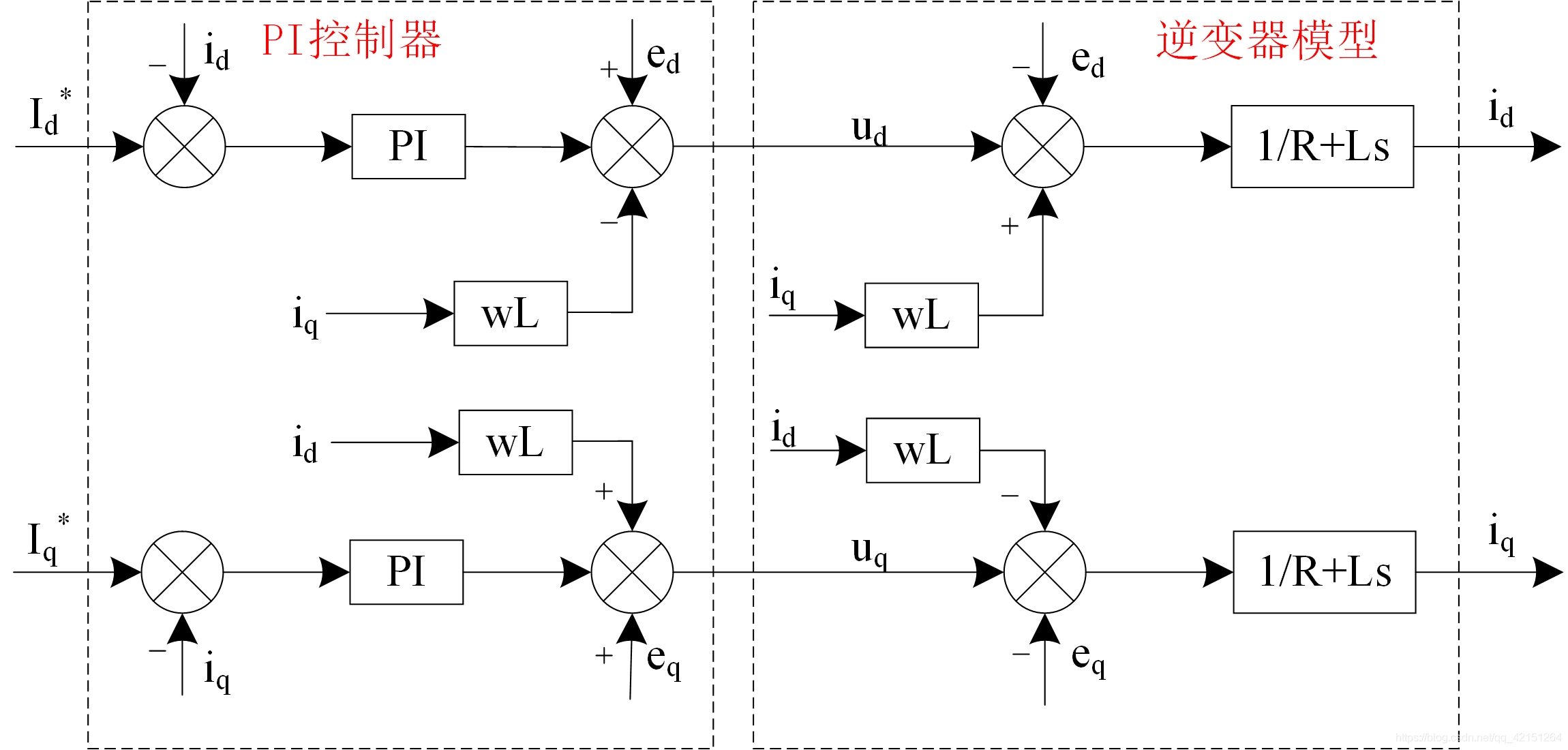

   According to this equation, we can build PI Current closed-loop control block diagram ：

   Some current models are bidirectional rectifier models in current control , That is, the current is defined as the flow of the power grid to the DC side . At this time, the circuit equation will change , The control block diagram will also happen . At this time, the control model is :
$$\{\begin{array}{c}{U}_d=-(Kp+\frac{Ki}{s})(i_d^{\ast }-i_d)+\omega L{i}_q+e_d\\ U_q=-(Kp+\frac{Ki}{s})(i_q^{\ast }-i_q)-\omega L{i}_d+e_q\end{array}$$
   Build the corresponding circuit according to the model .

5. Simulated main circuit

   According to the relevant parameters , Build the simulation main circuit :

Simulation results :

   Current amplitude given waveform :

Output current waveform :

Output power waveform

Model links

Model links , I need to take it myself ： Grid connected inverter PI control