(2022牛客多校五)D-Birds in the tree（树形DP）

题目：

样例输入：

7
1011111
1 2
1 3
2 4
3 5
2 6
4 7

样例输出：

28

题意：给定n个节点的树，树上每个节点的颜色为0或1，问最终有多少个子树的所有叶子颜色都是一样的。

分析：设f[i][0]代表以第i个节点为根的子树中度数为1（不包含根节点）的点颜色为0的子树数目,f[i][1]代表以第i个节点为根的子树中度数为1（不包含根节点）的点颜色为1的子树数目,先对数组的含义进行解释：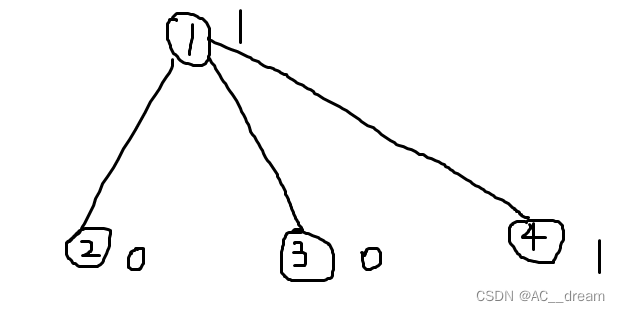

对于这张图而言，显然有

f[4][0]=0,f[4][1]=1

f[3][0]=1,f[3][1]=0

f[2][0]=1,f[2][1]=0

那么一号点呢？难道是合法状态数量，也就是f[1][1]=2,f[1][0]=1,其实不是，其实是f[1][1]=2,f[1][0]=3

注意我们f数组只对除了当前子树根节点以外其他度数为1的节点的颜色有明确要求，对根节点并没有要求，所以1-2，1-3也算是f[1][1]中的，当然这并不是合法的，但是这种情况却对更新上面的父节点有用，比如1的父节点是5，那么如果5的颜色是0，那么就可以通过5-1-2形成一个子树满足度为1的节点的颜色相同。当然，我们在统计答案的时候一定要减去这种不合法情况带来的影响，这种不合法情况有多少种呢？其实比较好统计，因为这种情况形成的子树其中根节点的度是1，也就是说他只会向他的一个子节点方向延伸，假如根节点颜色为1，那么他子节点j有多少f[j][0]就会有多少种不合法情况，把所有的子节点j的f[j][0]求一下和就是所有的不合法情况。但是大家会发现以1为根的子树中2-1-3是一个合法子树，那么这种情况我们怎么考虑到呢？其实很简单，比如对于上图而言，当前子树根节点1号节点有3个孩子节点，那么对于每一个孩子j可以贡献出f[j][0]种合法方案的一种，当然也可以不贡献，所以一共就会有f[j][0]+1种合法方案，那么对于所有的子节点都是这样的，我们最后只需要根据乘法原理求一个乘积就可以了，但是这样还会带来一个问题，比如我所有孩子节点都没有贡献怎么办？因为这种情况我们在一开始就已经初始化记录过了，所以这个时候我们还需要对答案减1，对应的就是所有子树中我们都不选的情况，最后就是别忘了我们需要统计一下以当前节点为根的子树中包含当前子树根节点且当前子树根节点度数为1的不合法情况，我们要将这种情况给排除掉，计算的方法我刚才已经进行了分析，细节见代码：

#include<cstdio>
#include<iostream>
#include<algorithm>
#include<cstring>
#include<map>
#include<queue>
#include<vector>
#include<cmath>
using namespace std;
const int N=3e5+10,mod=1e9+7;
int e[N*3],ne[N*3],h[N*3],idx;
long long f[N][2],ans;//f[i][0/1]代表以第i个节点为根的子树中度数为1（不包含根节点）的点颜色为0/1的子树数目 
char s[N];
int c[N];
void add(int x,int y)
{
	e[idx]=y;
	ne[idx]=h[x];
	h[x]=idx++;
}
void dfs(int x,int fa)
{
	f[x][0]=f[x][1]=0;//初始化 
	if(c[x]==1) f[x][1]=1;
	else f[x][0]=1;
	long long s0=1,s1=1,t0=0,t1=0;
	for(int i=h[x];i!=-1;i=ne[i])
	{
		int j=e[i];
		if(j==fa) continue;
		dfs(j,x);
		s0=s0*(f[j][0]+1)%mod;
		s1=s1*(f[j][1]+1)%mod;
		t0=(t0+f[j][0])%mod;
		t1=(t1+f[j][1])%mod;
	}
	f[x][0]=(f[x][0]+s0-1)%mod;//由子节点结合乘法原理得到，最后减去所有子节点上都取空的情况 
	f[x][1]=(f[x][1]+s1-1)%mod;
	ans=(ans+f[x][0]+f[x][1])%mod;
	if(c[x]==1)//如果根节点颜色为1，那么我们应该去掉一些子树根节点度数为1，但是其他度数为1的节点是0的情形 
		ans=((ans-t0)%mod+mod)%mod;
	else//如果根节点颜色为0，那么我们应该去掉一些子树根节点度数为1，但是其他度数为1的节点是1的情形
		ans=((ans-t1)%mod+mod)%mod;
}
int main()
{
	int n;
	while(scanf("%d",&n)!=EOF)
	{
		idx=ans=0;
		for(int i=1;i<=n;i++)
			h[i]=-1;
		scanf("%s",s+1);
		for(int i=1;i<=n;i++)
			c[i]=s[i]-'0';
		int u,v;
		for(int i=1;i<n;i++)
		{
			scanf("%d%d",&u,&v);
			add(u,v);add(v,u);
		}
		dfs(1,-1);
		printf("%lld\n",ans);
	}
	return 0;
}