当前位置:网站首页>CTF crypto RSA getting started
CTF crypto RSA getting started
2022-07-27 11:32:00 【There are fish in Beiming - its name is salty】
CTF CRYPTO RSA Introduction brush questions
cause : Because the college is going to hold a geek challenge , Yes CTF Knowing nothing, I was pulled in by three younger students to be a password player
This Saturday's game , You can only brush the questions temporarily before the competition
shooting range ( Question bank )
Along CRYPTO The topic goes on , This article only records some RSA Answer related questions , The order is point From too many people to too few
RSA
In a RSA Key pair generation , hypothesis p=473398607161,q=4511491,e=17
Find out d As flga Submit
rsa Introductory questions , Just know the principle , Don't explain
Code :
import gmpy2
p = 473398607161
q = 4511491
e = 17
phi = (p - 1) * (q - 1)
d = gmpy2.invert(e, phi)
print(d)
Get the answer flag{125631357777427553}
RSA1
p = 8637633767257008567099653486541091171320491509433615447539162437911244175885667806398411790524083553445158113502227745206205327690939504032994699902053229
q = 12640674973996472769176047937170883420927050821480010581593137135372473880595613737337630629752577346147039284030082593490776630572584959954205336880228469
dp = 6500795702216834621109042351193261530650043841056252930930949663358625016881832840728066026150264693076109354874099841380454881716097778307268116910582929
dq = 783472263673553449019532580386470672380574033551303889137911760438881683674556098098256795673512201963002175438762767516968043599582527539160811120550041
c = 24722305403887382073567316467649080662631552905960229399079107995602154418176056335800638887527614164073530437657085079676157350205351945222989351316076486573599576041978339872265925062764318536089007310270278526159678937431903862892400747915525118983959970607934142974736675784325993445942031372107342103852
It is known that p、q、dp、dp、c, Ask for clear text m
among dp、dq The meaning is as follows :
dp ≡ \equiv ≡ d (mod p-1)
dq ≡ \equiv ≡ d (mod q-1)
Principle Fermat's theorem + Chinese remainder theorem
See code for details
import gmpy2
p = 8637633767257008567099653486541091171320491509433615447539162437911244175885667806398411790524083553445158113502227745206205327690939504032994699902053229
q = 12640674973996472769176047937170883420927050821480010581593137135372473880595613737337630629752577346147039284030082593490776630572584959954205336880228469
dp = 6500795702216834621109042351193261530650043841056252930930949663358625016881832840728066026150264693076109354874099841380454881716097778307268116910582929
dq = 783472263673553449019532580386470672380574033551303889137911760438881683674556098098256795673512201963002175438762767516968043599582527539160811120550041
c = 24722305403887382073567316467649080662631552905960229399079107995602154418176056335800638887527614164073530437657085079676157350205351945222989351316076486573599576041978339872265925062764318536089007310270278526159678937431903862892400747915525118983959970607934142974736675784325993445942031372107342103852
n=p*q
m1 = gmpy2.powmod(c,dp,p)
m2 = gmpy2.powmod(c,dq,q)
p_inv = gmpy2.invert(p,q)
q_inv = gmpy2.invert(q,p)
m = gmpy2.powmod((q*q_inv*m1+p*p_inv*m2),1,n)
print(m)
print(hex(m))
print(bytes.fromhex(hex(m)[2:]))
RSA3
c1=22322035275663237041646893770451933509324701913484303338076210603542612758956262869640822486470121149424485571361007421293675516338822195280313794991136048140918842471219840263536338886250492682739436410013436651161720725855484866690084788721349555662019879081501113222996123305533009325964377798892703161521852805956811219563883312896330156298621674684353919547558127920925706842808914762199011054955816534977675267395009575347820387073483928425066536361482774892370969520740304287456555508933372782327506569010772537497541764311429052216291198932092617792645253901478910801592878203564861118912045464959832566051361
n=22708078815885011462462049064339185898712439277226831073457888403129378547350292420267016551819052430779004755846649044001024141485283286483130702616057274698473611149508798869706347501931583117632710700787228016480127677393649929530416598686027354216422565934459015161927613607902831542857977859612596282353679327773303727004407262197231586324599181983572622404590354084541788062262164510140605868122410388090174420147752408554129789760902300898046273909007852818474030770699647647363015102118956737673941354217692696044969695308506436573142565573487583507037356944848039864382339216266670673567488871508925311154801
e1=11187289
c2=18702010045187015556548691642394982835669262147230212731309938675226458555210425972429418449273410535387985931036711854265623905066805665751803269106880746769003478900791099590239513925449748814075904017471585572848473556490565450062664706449128415834787961947266259789785962922238701134079720414228414066193071495304612341052987455615930023536823801499269773357186087452747500840640419365011554421183037505653461286732740983702740822671148045619497667184586123657285604061875653909567822328914065337797733444640351518775487649819978262363617265797982843179630888729407238496650987720428708217115257989007867331698397
e2=9647291
subject : Know the same plaintext m In different keys e1、e2 The result of encryption , Ask for clear text m
principle : Common mode attack ,e1、e2 It's reciprocal , Use extended Euclidean to find e1x+e2y=1, And then put m The power of becomes 1 that will do , Don't forget x or y When it is less than zero, take the modulus inverse
Code :
import gmpy2
c1 = 22322035275663237041646893770451933509324701913484303338076210603542612758956262869640822486470121149424485571361007421293675516338822195280313794991136048140918842471219840263536338886250492682739436410013436651161720725855484866690084788721349555662019879081501113222996123305533009325964377798892703161521852805956811219563883312896330156298621674684353919547558127920925706842808914762199011054955816534977675267395009575347820387073483928425066536361482774892370969520740304287456555508933372782327506569010772537497541764311429052216291198932092617792645253901478910801592878203564861118912045464959832566051361
n = 22708078815885011462462049064339185898712439277226831073457888403129378547350292420267016551819052430779004755846649044001024141485283286483130702616057274698473611149508798869706347501931583117632710700787228016480127677393649929530416598686027354216422565934459015161927613607902831542857977859612596282353679327773303727004407262197231586324599181983572622404590354084541788062262164510140605868122410388090174420147752408554129789760902300898046273909007852818474030770699647647363015102118956737673941354217692696044969695308506436573142565573487583507037356944848039864382339216266670673567488871508925311154801
e1 = 11187289
c2 = 18702010045187015556548691642394982835669262147230212731309938675226458555210425972429418449273410535387985931036711854265623905066805665751803269106880746769003478900791099590239513925449748814075904017471585572848473556490565450062664706449128415834787961947266259789785962922238701134079720414228414066193071495304612341052987455615930023536823801499269773357186087452747500840640419365011554421183037505653461286732740983702740822671148045619497667184586123657285604061875653909567822328914065337797733444640351518775487649819978262363617265797982843179630888729407238496650987720428708217115257989007867331698397
e2 = 9647291
gcd, x, y = gmpy2.gcdext(e1, e2)
if x < 0:
x = -x
c1 = gmpy2.invert(c1, n)
if y < 0:
y = -y
c2 = gmpy2.invert(c2, n)
ans = gmpy2.powmod(c1, x, n) * gmpy2.powmod(c2, y, n) % n
print(ans)
print(hex(ans))
print(bytes.fromhex(hex(ans)[2:]))
RSA2
subject :
e = 65537
n = 248254007851526241177721526698901802985832766176221609612258877371620580060433101538328030305219918697643619814200930679612109885533801335348445023751670478437073055544724280684733298051599167660303645183146161497485358633681492129668802402065797789905550489547645118787266601929429724133167768465309665906113
dp = 905074498052346904643025132879518330691925174573054004621877253318682675055421970943552016695528560364834446303196939207056642927148093290374440210503657
c = 140423670976252696807533673586209400575664282100684119784203527124521188996403826597436883766041879067494280957410201958935737360380801845453829293997433414188838725751796261702622028587211560353362847191060306578510511380965162133472698713063592621028959167072781482562673683090590521214218071160287665180751
subject : It is known that e、n、dp、c, Ask for clear text
Ideas : Let's start with the links , I'll fill in details later : Answer key
Code :
import gmpy2
e = 65537
n = 248254007851526241177721526698901802985832766176221609612258877371620580060433101538328030305219918697643619814200930679612109885533801335348445023751670478437073055544724280684733298051599167660303645183146161497485358633681492129668802402065797789905550489547645118787266601929429724133167768465309665906113
dp = 905074498052346904643025132879518330691925174573054004621877253318682675055421970943552016695528560364834446303196939207056642927148093290374440210503657
c = 140423670976252696807533673586209400575664282100684119784203527124521188996403826597436883766041879067494280957410201958935737360380801845453829293997433414188838725751796261702622028587211560353362847191060306578510511380965162133472698713063592621028959167072781482562673683090590521214218071160287665180751
p = q = 0
for x in range(1, e):
if (dp * e - 1) % x == 0 and n % (((dp * e - 1) // x) + 1) == 0:
p = ((dp * e - 1) // x) + 1
q = n // p
phi = (p - 1) * (q - 1)
d = gmpy2.invert(e, phi)
m = gmpy2.powmod(c, d, n)
print(m)
print(hex(m))
print(bytes.fromhex(hex(m)[2:]))
The answer is :flag{wow_leaking_dp_breaks_rsa?_98924743502}
边栏推荐
- 深析C语言的灵魂 -- 指针
- 博弈论 AcWing 892. 台阶-Nim游戏
- 数字三角形模型 AcWing 1018. 最低通行费
- 背包模型 AcWing 1024. 装箱问题
- Moveit2 -- 2. Quick start of moveit in rviz
- What is the issuing price of NFT (Interpretation of NFT and establishment of NFT world outlook)
- 求组合数 AcWing 885. 求组合数 I
- Luogu p3052 [usaco12mar]cows in a skyscraper G
- Installation and use of GTEST and gmock
- Solutions to errors in tensorflow operation
猜你喜欢
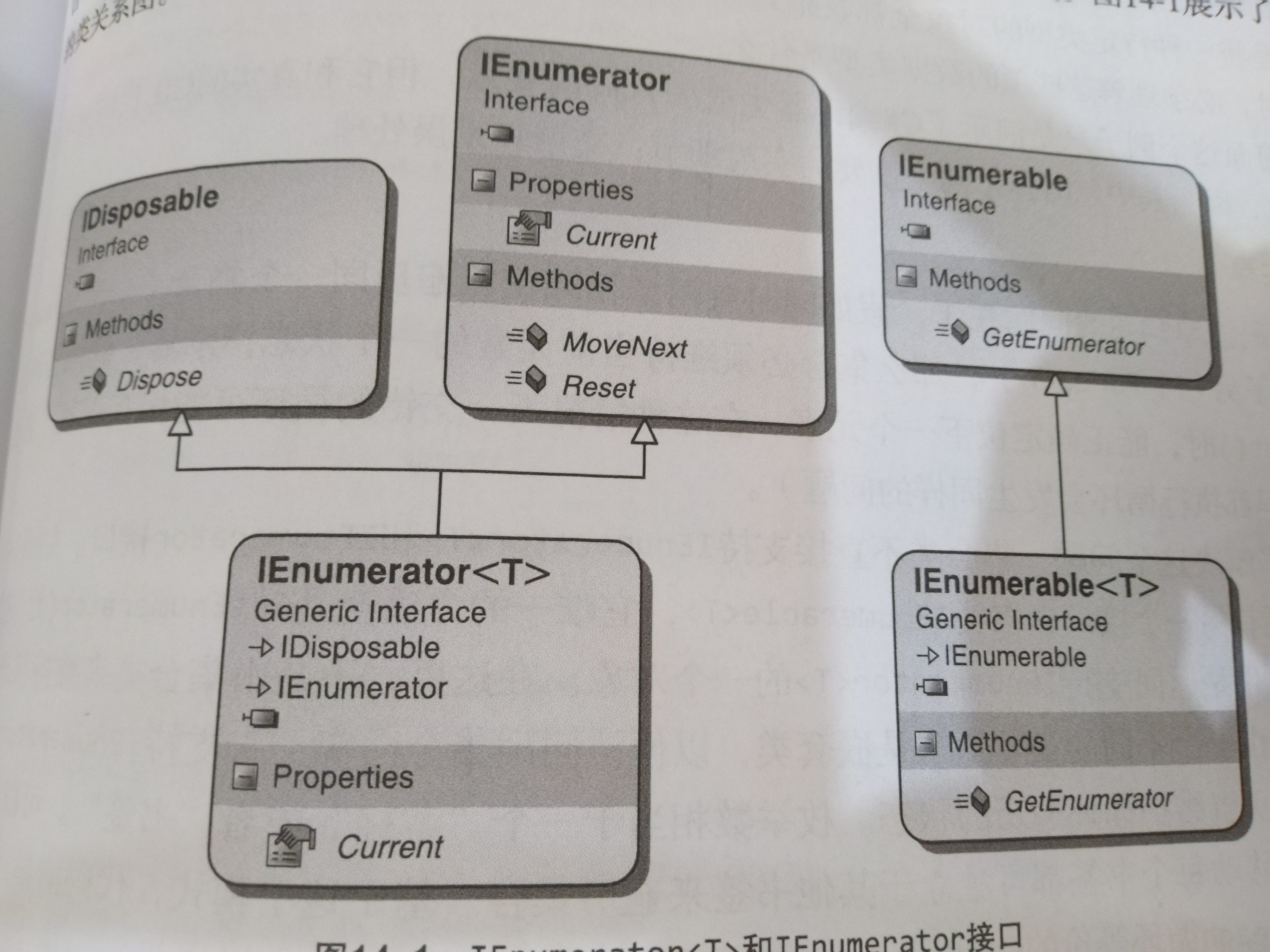
C custom set

最长上升子序列模型 AcWing 1016. 最大上升子序列和

背包模型 AcWing 423. 采药

Gaussian elimination acwing 883. solving linear equations with Gaussian elimination

记忆化搜索 AcWing 901. 滑雪

Find the combination number acwing 886. find the combination number II

49 letter ectopic grouping and 242 effective letter ectopic words
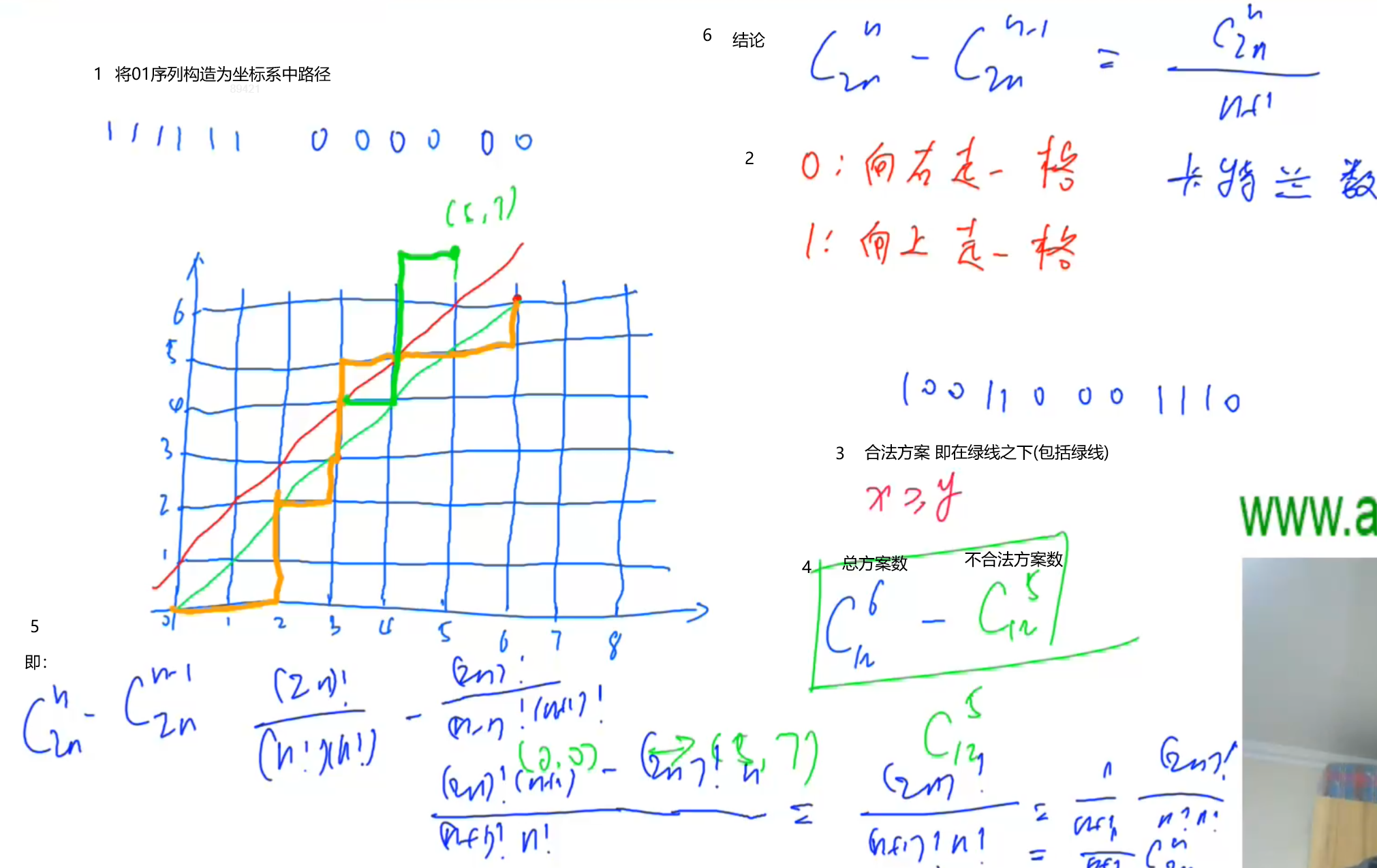
Find the combinatorial number acwing 889. 01 sequence satisfying the condition

Analysis of distributed database and cache double write consistency scheme (Reprint)

Find the combination number acwing 888. find the combination number IV
随机推荐
tensorflow运行报错解决方法
"My" bug collection (Reprinted)
Lazy loading of lists and pictures
Knapsack model acwing 423. Picking herbs
Game theory acwing 891. Nim game
Force buckle - 10. Regular expression matching
深析C语言的灵魂 -- 指针
49字母异位分组和242有效的字母异位词
求组合数 AcWing 887. 求组合数 III
Instructions for mock platform
349两个数组的交集和01两数之和
(10) File contains
What is the issuing price of NFT (Interpretation of NFT and establishment of NFT world outlook)
Longest ascending subsequence model acwing 1014. mountaineering
2022牛客多校训练(3)A-Ancestor 题目翻译
Description and feelings
01 BTC cryptology principle
Introduction to software vulnerability analysis (I)
Moveit2 - 4. robot model and robot state
数字三角形模型 AcWing 1015. 摘花生