Application of four ergodic square of binary tree

Want to make APP Same thing as WeChat , Can run small programs smoothly ？ | Experience will send you to Xinjiang 、 Huawei 、 Cherry keyboard ！>>>

Preface

In the last chapter we started with 0 To 1 The implementation of a binary search tree , And understand the characteristics and basic operation of binary search tree , This chapter introduces more about binary trees , That's tree traversal , Access to each node of the tree . It mainly includes preorder traversal 、 In the sequence traversal 、 After the sequence traversal 、 Sequence traversal , The first three are also called depth first traversal (DFS), The last sequence traversal is also called breadth first traversal (BFS), Understand the differences between these four traversal methods , When we encounter the tree related algorithm problem again , And you can be more comfortable . It's not just a binary search tree , The idea of traversal also applies to multitree .

Depth-first traversal (DFS)

Depth first, as the name suggests , Start with the depth of the tree , That is, visit one of the subtrees first , And then visit another subtree . The depth priority of the tree is divided into the front / in / After the sequence traversal , The only difference between them is when accessing a specific node , They are different in order . Depth first is usually implemented recursively , Because it's easy to understand , Of course, you can also use traversal to implement , But that will increase the complexity of the code and the semantics of the code .(LeetCode The non recursive implementation of up and down traversal is difficult )

The former sequence traversal

In other words, access the node of the tree from the front , First post the code , Add the method of preorder traversal to the binary search tree implemented in the previous chapter ：

 

Use one prev Variables cache the last visited node , Each time, let the current access node value minus the previous node value , Because it's a middle order traversal , So the value of the current node must be greater than that of the previous node , Go through the whole tree , Return the minimum value of subtraction .

After the sequence traversal

Just change the location of the access node , Visit the left subtree first , Visit the right subtree , Finally, visit its own root node , Post code ：

class BST {
  constructor() {
    this.root = null //  The root node 
  }
  ...
  
  postorder(fn) { //  After the sequence traversal 
  	const _helper = node => {
      if (!node) {
        return
      }
      _helper(node.left) //  First visit the left child 
      _helper(node.right) //  And then interview the right child 
	  fn(node.val) //  Finally, the root node is accessed       
    }
    _helper(root)
  }
}

First visit the left subtree , And then the right subtree , Finally, there is the node itself , The order of access is as follows ：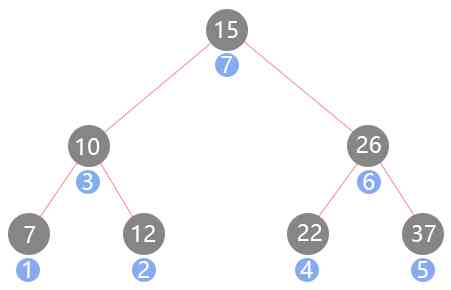 

Postorder traversal applications - 563- The slope of the binary tree

 Given a binary tree , Calculate the slope of the whole tree .
 The slope of a tree node is defined as , The absolute value of the difference between the sum of the nodes of the left subtree and the sum of the nodes of the right subtree . The slope of the empty node is 0.
 The slope of the whole tree is the sum of the slopes of all its nodes .

In short, the slope of each node is equal to the absolute difference between the sum of its left and right subtrees , So the slope of the leaf node is 0, Because the left and right children are empty nodes , Back to you 0-0 Value . If we disassemble the subproblem , It can be understood that the slope of the whole tree is the sum of the slopes of its left and right sub trees , Therefore, it is necessary to calculate the slope of the left and right children before calculating the slope of the current node , Post order traversal is very suitable for . 
The solution code is as follows ：

var findTilt = function (root) {
  let tilt = 0
  const _helper = (node) => {
    if (!node) {
      return 0 //  The slope of leaf node is 0
    }
    const l = _helper(node.left) //  First find the sum of the left subtree 
    const r = _helper(node.right) //  Then find the sum of the right subtree 
    tilt += Math.abs(l - r) //  The slope of the current node is equal to the absolute difference between the sum of the left and right subtrees 
    return l + r + node.val //  Return to the subtree and 
  }
  _helper(root)
  return tilt
};

Depth-first traversal (DFS) Advanced application

The above three algorithms , The front of the tree is shown separately / in / The practical application of postorder traversal , That's not enough . Some algorithmic problems can not be solved by the conventional traversal method , At this time, we need to deeply understand the tree's (DFS) After traversing the properties , Make extra flexible processing to solve .

Anti normal ordinal traversal - 538- Convert binary search tree to accumulation tree

 Given a binary search tree , Turn it into an accumulation tree , So that the value of each node is the sum of the original node value plus all nodes greater than it .

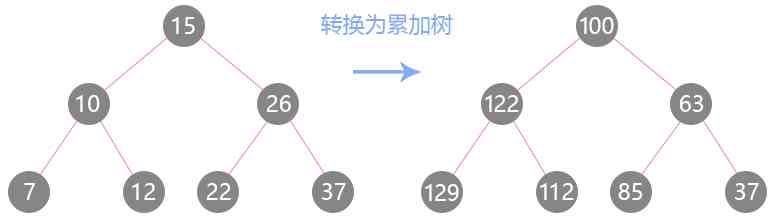
The topic is not easy to understand , But as you can see from the example of the transformation , Start with the rightmost leaf node of the right subtree , Add the node values in pairs , Finally, the whole tree is accumulated from right to left . If you think of this binary search tree as an array [7,10,12,15,22,26,37], Then its operation is to add the array from back to front and cover the previous value . For trees , We need to do an unconventional middle order traversal , First, traverse the right subtree , Then traverse the root node , Finally, traverse the left subtree , That is, a descending traversal .

var convertBST = function (root) {
  let sum = 0
  const _helper = (node) => {
    if (!node) {
      return null
    }
    _helper(node.right) //  First traverse the right subtree 
    node.val += sum //  After the right subtree to the bottom, the values are accumulated and covered one by one 
    sum = node.val //  It records the value of the last node that was covered 
    _helper(node.left) //  Finally, traverse the left subtree 
  }
  _helper(root)
  return root //  Returns a new cumulative tree 
};

Preorder and postorder traversal - 257- All paths of binary tree

 Given a binary tree , Return all paths from the root node to the leaf node .

The requirement of the title is from the root node to the leaf node , So record the current node of each step , The order of preorder traversal can record the entire path from root to leaf node . The interesting thing about this problem is that when the preorder traversal returns , The last leaf node needs to be removed from the path , Re add another node path value , So it can be in the order of post traversal , Like a greedy snake, you eat the paths you have visited . Some people take this solution to a very powerful, called backtracking . The code is as follows ：