Improved schemes for episodic memory based lifelong learning

The address of the paper is here

One . Introduce

At present, deep neural network can achieve remarkable performance on a single task , However, when the network is retrained to a new task , His performance has fallen sharply on previously trained tasks , This phenomenon is called catastrophic forgetting . In sharp contrast to it is , The human cognitive system can acquire new knowledge without destroying previous knowledge .
Catastrophic forgetting has inspired the field of lifelong learning . One of the core problems of lifelong learning is how to strike a balance between old tasks and new tasks . In the process of learning new tasks , The knowledge learned in the past is usually disturbed , Leading to catastrophic forgetting . On the other hand , Learning algorithms that favor old tasks will interfere with the learning of new tasks . In this scenario , At present, several strategies are proposed . Including regularization based methods , Methods based on knowledge transfer and episodic memory . Especially in the method based on episodic memory , Such as gradient episodic memory （GEM） And average gradient episodic memory （A-GEM） Realize significant performance . In episodic memory , Use small episodic memory to store instances in old tasks , To guide the optimization of the current task .
In this paper the author , From the perspective of optimization, this paper puts forward the viewpoint of lifelong learning method based on episodic memory （ in the light of GEM and A- GEM）. The optimization problem is approximately solved by using one-step random gradient descent method , The standard gradient is replaced by the mixed random gradient method . At the same time, two different schemes are proposed ,MEGA-1,MEGA-2, It can be used in different scenarios .

Two . Related work

Regularization based approach ： Classical method EWC use fisher information The matrix prevents the weight of old tasks from changing dramatically .PI in , The author introduces the intelligent synapse , And give each prominent local importance measure , To avoid old memories being overwritten .R-WALK Based on KL Divergent regularization to preserve knowledge of old tasks . And in the MAS in , The importance measure of each parameter of the network is calculated based on the sensitivity of the predictive output function to parameter changes .
Based on the way of knowledge transfer ： stay PROG-NN in , Add a new column for each task , This column is connected to the hidden layer of the previous task . meanwhile , There is also the use of unmarked （ not used ） Data to avoid catastrophic forgetting , That is, knowledge distillation .
Based on episodic memory ： Using external memory to enhance standard neural networks is a widely adopted practice . In the method of lifelong learning based on episodic memory , A small reference memory is used to store information from old tasks . When the angle between the current gradient and the gradient calculated on the reference memory is an obtuse angle ,GEM and A-GEM Rotate the current gradient .
The scheme proposed by the author aims to improve the method based on episodic memory . And A-GEM Different , The scheme explicitly considers the performance of the model for old tasks and new tasks in the current gradient rotation process .

3、 ... and . Lifelong learning

Lifelong learning considers the problem of learning new tasks without reducing the performance of old tasks to avoid catastrophic forgetting . Suppose there is T Tasks correspond to T Data sets ：$\{D_1,D_2,...,D_T\}$. Every data set $D_t$ Is a tuple $\{x_i,y_i,t\}$ A list of components . Similar to supervised learning , Every data set $D_t$ It can be divided into training sets $D_t^{tr}$ And test set $D_t^{te}$.
stay A-GEM in , Tasks are divided into $D^{CV}=\{D_1,D_2,...,D_{T^{CV}}\}$ and $D^{EV}=\{D_{T^{CV}+1}{D}_{T^{CV}+2},...,D_T\}$. among $D^{CV}$ Used for cross validation to search for super parameters .$D^{EV}$ For practical training and evaluation . When searching for super parameters , We can do it in $D^{CV}$ The example is propagated many times in , stay $D^{EV}$ On the execution of training , Pass the example only once .
In lifelong learning , A model $f(x;w)$ Trained in a series of tasks $\{D_{T^{CV}+1},D_{T^{CV}+2},...,D_T\}$. When the model is trained to the task $D_t$, The goal is to predict $D_t^{te}$ By minimizing $D_t^{tr}$ Experience loss $l_t(w)$ Not lower in $\{D_{T^{CV}+1}^{te},D_{T^{CV}+2}^{te},...,D_{t-1}^{te}\}$

Four . The view of lifelong learning based on episodic memory

GEM and A-GEM By using a small episodic memory $M_k$ To store tasks k A subset of the examples in . Episodic memory is filled by randomly and evenly selecting examples for each task . When training on mission $t$ when , The loss of episodic memory can be calculated as :$l_{ref}(w_t;M_k)=\frac{1}{|M_k|}{\sum }_{(x_i,y_i)\in M_k}l(f(x_i;w_t),y_i)$.
stay GEM and A-GEM in , Training lifelong learning model by small batch random gradient descent method . We use $w_k^t$ Expressed as a model in the task t Is the awkward part of the training to the k individual mini-batch The weight of . In order to establish the old task with the t Performance tradeoffs for tasks , We consider the following compound objective optimization problem in each update step ：
$$\underset{w}{\min }{\alpha }_1(w_k^t)l_t(w)+{\alpha }_2(w_k^t)l_{ref}(w)={\mathbb{E}}_{\xi ,\zeta }[{\alpha }_1(w_k^t)l_t(w;\xi )+{\alpha }_2(w_k^t)l_{ref}(w;\zeta )]$$
among $\xi ,\zeta$ Represents a random vector with finite support ,$l_t(w)$ For the first time t Training loss of missions ,$l_{ref}(w)$ Is the predicted loss calculated from the data stored in the episodic memory ,${\alpha }_1(w),{\alpha }_2(w)$ For control at each mini-batch in $l_t(w)$ and $l_{ref}(w)$ The relative importance of .
So mathematically , We can consider using the following updates ：
$$w_{k+1}^t=arg\underset{w}{\min }{\alpha }_1(w_k^t)l_t(w;\xi )+{\alpha }_2(w_k^t)l_{ref}(w;\zeta )$$
GEM and A- GEM The first-order method （ Random gradient ） Approximate optimization of the above formula , One step of the random gradient is from the initial point $w_k^t$ At the beginning ：
$$w_{k+1}^t=w_k^t-\eta ({\alpha }_1(w_k^t)\nabla l_t(w;\xi )+{\alpha }_2\nabla (w_k^t)l_{ref}(w;\zeta ))$$
stay GEM and A-GEM in ${\alpha }_1(w)$ by 1, This means that the current task is always given the same attention during training , No matter how the loss changes with time . In the process of lifelong learning , Current losses and scenario losses are dynamic in each small batch , And if the ${\alpha }_1(w)$ Always be 1 May not strike a good balance .

5、 ... and . Mixed random gradient

In this section , The authors introduce the mixed random gradient (MEGA) To solve GEM and A-GEM The limitations of . because A-GEM Better performance than GEM, use A- GEM To calculate the scenario reference loss .

5.1 MEGA-I

MEGA-I It is an adaptive loss based method , Balance the current task with the old task by using only the loss information . The author introduces a predefined sensitive parameter $ϵ$. as follows ：
$$\{\begin{array}{ll}{\alpha }_1(w)=1,{\alpha }_2(w)=l_{ref}(w;\zeta )/l_t(w;\xi )& \text{if }{l}_t(w;\xi )>ϵ\\ {\alpha }_1(w)=0,{\alpha }_2(w)=1& \text{if }{l}_t(w;\xi )<=ϵ\end{array}$$
Intuitively , If the model performs well on the current task （ That is to say loss Very small ）, that MEGA-I Focus on improving the performance of data stored in episodic memory . Because of the choice ${\alpha }_1(w)=0,{\alpha }_2(w)=1$. otherwise , When the loss is large ,MEGA-I Then keep the equilibrium of these two mixed random gradients through $l_{ref}(w;\zeta ),l_t(w;\xi )$.

5.2 MEGA-II

MEGA-I The size of the blending gradient depends on the current gradient and the scenario related gradient , And the loss of current tasks and episodic memory . and MEGA-II The mixed gradient of is lost A- GEM Inspired by the , From the rotation of the current gradient , Its size depends only on the current gradient .
MEGA-II Firstly, the random gradient calculated by the current task is rotated properly , Through an angle ${\theta }_k^t$. Then the rotated vector is used as a mixed random gradient , Update each small batch .
We use $g_{mix}$ To represent the desired mixed random gradient , The size and the $\nabla l_t(w;\xi )$ equally . We're looking for directions that match $\nabla l_t(w;\xi ),\nabla l_{ref}(w;\zeta )$. And MEGA-I similar , We use the loss balancing scheme and want to maximize it ：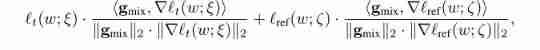

Look for the following $\theta$:
$$\theta =arg\underset{\beta \in [0,\pi ]}{\max }{l}_t(w;\xi )cos(\beta )+l_{ref}(w;\xi )cos(\tilde{\theta }-\beta )$$
among $\tilde{\theta }\in [0,\pi ]$ For in $\nabla l_t(w;\xi )$ To $\nabla l_{ref}(w;\zeta )$ The angle between ,$\beta \in [0,\pi ]$ For in $g_{mix}$ and $\nabla l_t(w;\xi )$ The angle between . among $\theta$ The closed form of is $\theta =\frac{\pi }{2}-\alpha$, among $\alpha =arctan(\frac{k+cos\tilde{\theta }}{sin\tilde{\theta }}),k=l_t(w;\xi )/l_{ref}(w;\zeta )$.

Here are some special cases

When $l_{ref}(w;\zeta )=0$, here $\theta =0$, under these circumstances ${\alpha }_1(w)=1,{\alpha }_2(w)=0$. This means no forgetting , So learn new tasks directly .

When $l_t(w;\xi )=0$, here $\theta =\tilde{\theta }$, under these circumstances ${\alpha }_1(w)=0$, ${\alpha }_2(w)=||\nabla l_t(w;\xi )|{|}_2/||\nabla l_{ref}(w;\zeta )|{|}_2$. In this case , The direction of the mixed random gradient is the same as that of the random gradient calculated from the data in the episodic memory .

6、 ... and . Key code interpretation

Code point here
The author's code is very complicated , Integrate a variety of lifelong learning methods , The algorithm proposed by the author of this paper is mainly aimed at GEM and A-GEM Medium ${\alpha }_1(w)$ and ${\alpha }_2(w)$ Make changes , So the code section only describes this part , and GEM Part I will use other codes to cooperate with the thesis to explain .MEGA-II Can be said to be MEGA-I A more applicable version of , We will explain this .
First , Explicit parameters , According to the above, when our model carries out back propagation , We can get $\nabla l_t(w;\xi )$ and $\nabla l_{ref}(w;\zeta )$, For the convenience of writing , Write them down as $g_t$ and $g_r$（ The corresponding loss is recorded as $l_t,l_r$）. Again MEGA-II in ,$\tilde{\theta }$ by $g_t$ and $g_r$ The angle between :
$$\tilde{\theta }=arccos(\frac{g_t\ast g_r}{||g_t|{|}_2\ast ||g_r|{|}_2})$$
The corresponding code is as follows ：

##  Multiply the distances of two vectors 
self.deno1 = (tf.norm(flat_task_grads) * tf.norm(flat_ref_grads))
##  Multiply two vectors 
self.num1 = tf.reduce_sum(tf.multiply(flat_task_grads, flat_ref_grads))
##  Find the angle 
self.angle_tilda = tf.acos(self.num1/self.deno1)

Then there was $\tilde{\theta }$ after , We can update $\theta$ 了 , Here we use a gradient to update .
set up $k=\frac{l_r}{l_t}$, We solve it $\theta$ The formula becomes ：
$$\theta =arg\underset{\beta }{\max }[cos(\beta )+k\ast cos(\tilde{\theta }-\beta )]$$
Gradient update ( Due to time demand argmax Therefore, it is used + Number )
$$\theta =\theta +[-sin(\theta )+k\ast sin(\tilde{\theta }-\theta )]$$
$\theta$ For the range of $[0,\frac{\pi }{2}]$( Here the author gives proof )

Therefore, we need to prevent overflow after updating .
The corresponding code is ：

def loop(steps, theta):
	## \theta The calculation of , It is worth noting that , The author also * On a 1/(1+k), there self.ratio The corresponding is k
	theta =  theta + (1 / (1+self.ratio)) * (-tf.sin(theta) + self.ratio * tf.sin(self.angle_tilda - theta))
	##  Prevent exceeding the range 
	theta = tf.cond(tf.greater_equal(theta, 0.5*pi), lambda: tf.identity(0.5*pi), lambda: tf.identity(theta))
	theta = tf.cond(tf.less_equal(theta, 0.0), lambda: tf.identity(0.0), lambda: tf.identity(theta))
	steps = tf.add(steps, 1)

The author has solved many times here $\theta$, by ：

for idx in range(3):    
    steps = tf.constant(0.0)

    _, thetas[idx] = tf.while_loop(
        condition,
        loop,
        [steps, thetas[idx]]
    )
    
    objectives[idx] = self.old_task_loss * tf.cos(thetas[idx]) + self.ref_loss * tf.cos(self.angle_tilda - thetas[idx])

objectives = tf.convert_to_tensor(objectives)
max_idx = tf.argmax(objectives)
self.theta = tf.gather(thetas, max_idx)

Finally, according to $\theta$ solve ${\alpha }_1$ and ${\alpha }_2$ 了 , Here the author also gives the solution ：

That is, simultaneous equations a and b that will do , The corresponding code is as follows ：

tr = tf.reduce_sum(tf.multiply(flat_task_grads, flat_ref_grads))
tt = tf.reduce_sum(tf.multiply(flat_task_grads, flat_task_grads))
rr = tf.reduce_sum(tf.multiply(flat_ref_grads, flat_ref_grads))
def compute_g_tilda(tr, tt, rr, flat_task_grads, flat_ref_grads):
    a = (rr * tt * tf.cos(self.theta) - tr * tf.norm(flat_task_grads) * tf.norm(flat_ref_grads) * tf.cos(self.angle_tilda-self.theta)) / self.deno
    b = (-tr * tt * tf.cos(self.theta) + tt * tf.norm(flat_task_grads) * tf.norm(flat_ref_grads) * tf.cos(self.angle_tilda-self.theta)) / self.deno
    return a * flat_task_grads + b * flat_ref_grads
self.deno = tt * rr - tr * tr            
g_tilda = tf.cond(tf.less_equal(self.deno, 1e-10), lambda: tf.identity(flat_task_grads), lambda: compute_g_tilda(tr, tt, rr, flat_task_grads, flat_ref_grads))

To go here about MEGA-II And we're done , Author combination A-GEM The rotation angle is used to balance the loss of old tasks and the loss of new tasks , It can be used for reference .