当前位置:网站首页>EFFICIENT PROBABILISTIC LOGIC REASONING WITH GRAPH NEURAL NETWORKS
EFFICIENT PROBABILISTIC LOGIC REASONING WITH GRAPH NEURAL NETWORKS
2022-07-03 10:32:00 【kormoie】
EFFICIENT PROBABILISTIC LOGIC REASONING WITH GRAPH NEURAL NETWORKS( Use neural network to carry out effective probabilistic logic reasoning )
Introduce :
Because the knowledge map is incorrect 、 Incomplete or duplicate data , Therefore, it is very important to complete the knowledge map . This paper uses Markov logic network Markov Logic Networks (MLNs) And graph neural networks graph neural networks (GNNs) Combined with variational reasoning based on knowledge map , And put forward GNN A variation of the ,ExpressGNN.ExpressGNN Strike a good balance between model expressiveness and simplicity .Markov Logic Networks (MLNs):
Markov logic network combines hard logic rules and probability graph model , It can be applied to various tasks of knowledge map . Logical rules combine prior knowledge , allow MLNS Promote in tasks with a small amount of labeled data . Graphical models provide a principled framework for dealing with uncertain data . However ,MLN The reasoning in is computationally intensive , Generally, the number of entities increases exponentially , Limited real-world applications . Logical rules can only cover a small part of the possible combination of knowledge graph relationships , Therefore, it limits the application of models based purely on logical rules .
Graph neural networks (GNNs):
GNN Effectively solve many graph related problems .GNN It is required to have enough tag data applied to specific end tasks to achieve good performance , However, the knowledge map has a long tail problem . The problem of data scarcity in this long tail relationship poses a severe challenge to the pure data-driven approach .
The article explores a combination MLNs and GNN A data-driven method that can utilize prior knowledge encoded in logical rules . This paper designs a simple graph neural network ExpressGNN, To effectively train in variation EM Under the framework of MLN.

Related work :
Statistical relational learning
Markov Logic Networks
Graph neural networks
Knowledge graph embedding
The main method :
- data
Knowledge map triplet K = (C,R,O)
Set of entities C = (c1,…, cM)
Relational sets R =(r1,…, rN)
A collection of observable facts O = (o1,…,oL).
Entities are constants , Relation is also called predicate . Every predicate uses C Defined logic function . For a specific set of entities assigned to parameters , The predicate is called ground The predicate . Each predicate has ground predicate = a binary random variable.
ar = (c,c0), be ground The predicate r(c, c0) Can be expressed as r(ar)
Every observed fact uses truth {0,1} Represent and assign to ground predicate.
For example, a fact o It can be expressed as [L(c; c0) = 1].
Because there are far more unobserved facts than observed facts , therefore unobserved facts = latent variables
More clearly , as follows :
For a knowledge map K, Express with complete bipartite graph GK = (C,O,E), Set of constants C, Observable facts O, Side set E=(e1,…, eT), such as edge e = (c,o,i), At node c and o between .
And o The relevant predicate is in the i Parameter positions are used c As a parameter , Pictured 2 Of GK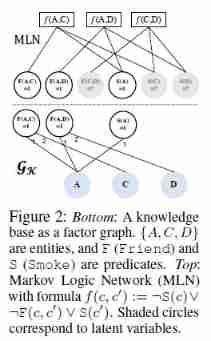
Markov logic network uses logic formula to define potential function in undirected graph model .
The form of a logical formula :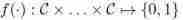
A binary function defined by a combination of several predicates .
such as f(c, c0) Can be expressed as 
Similar to predicates , We mean to assign a constant to the formula f The parameters of are expressed as af, The entire set of constant consistent assignments 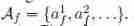
The joint probability distribution of observable facts and observed facts :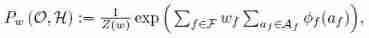
KG and MLN Different :KG sparse ,MLN dense .
EM Maximum expectation algorithm
VARIATIONAL EM FOR MARKOV LOGIC NETWORKS
Markov logic network establishes the joint probability distribution model of all observed variables and potential variables . This model can be trained by maximizing the log likelihood of all observed facts . It is difficult to directly maximize the goal , Because it needs to calculate the partition function and integrate all H and O Variable . therefore , We optimize the lower bound of variational evidence for log likelihood of data (ELBO), As shown below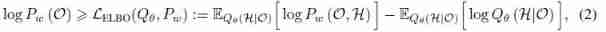
E Step ---- Reasoning

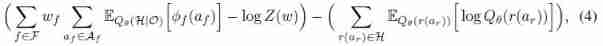
Add a supervised learning goal to enhance the reasoning network :
Objective function :
- M Step ---- Study

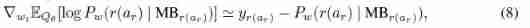
- ExpressGNN

experiment :
reference :
边栏推荐
- Hands on deep learning pytorch version exercise solution -- implementation of 3-2 linear regression from scratch
- A complete mall system
- ThreadLocal原理及使用场景
- Hands on deep learning pytorch version exercise answer - 2.2 preliminary knowledge / data preprocessing
- Inverse code of string (Jilin University postgraduate entrance examination question)
- 深度学习入门之线性代数(PyTorch)
- Leetcode刷题---977
- Neural Network Fundamentals (1)
- Anaconda安装包 报错packagesNotFoundError: The following packages are not available from current channels:
- Mise en œuvre d'OpenCV + dlib pour changer le visage de Mona Lisa
猜你喜欢

An open source OA office automation system
3.1 Monte Carlo Methods & case study: Blackjack of on-Policy Evaluation
熵值法求权重
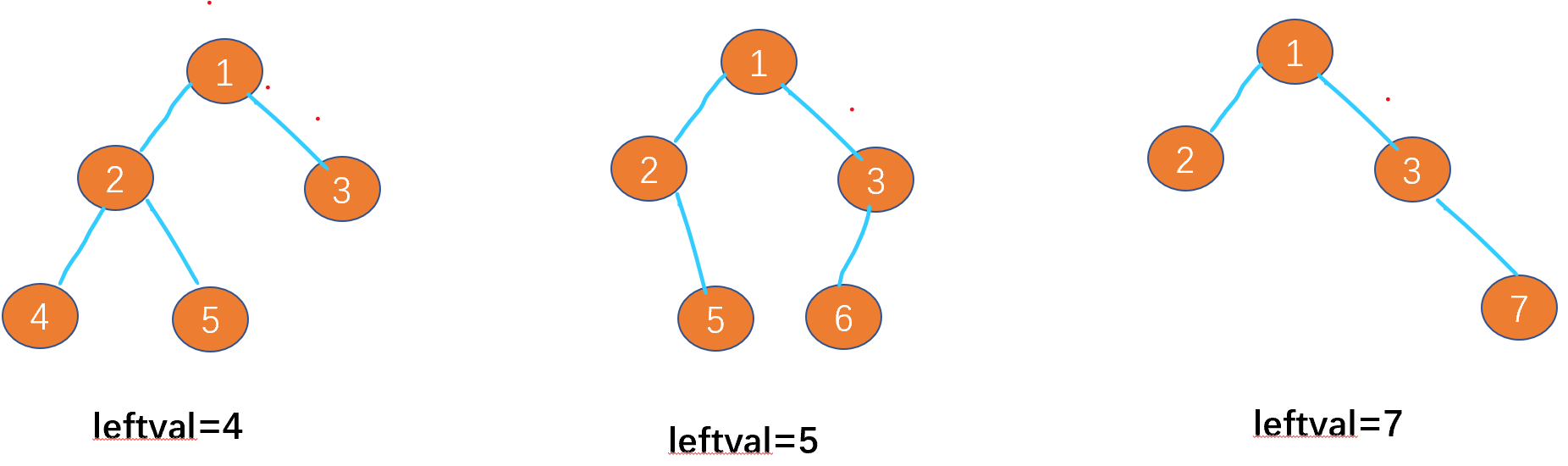
Leetcode-513: find the lower left corner value of the tree

八、MySQL之事务控制语言
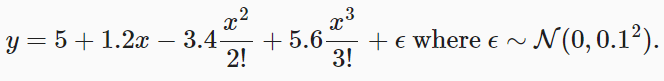
神经网络入门之模型选择(PyTorch)

What can I do to exit the current operation and confirm it twice?

Leetcode - 5 longest palindrome substring

Leetcode-106: construct a binary tree according to the sequence of middle and later traversal

七、MySQL之数据定义语言(二)
随机推荐
Realize an online examination system from zero
Tensorflow—Neural Style Transfer
实战篇:Oracle 数据库标准版(SE)转换为企业版(EE)
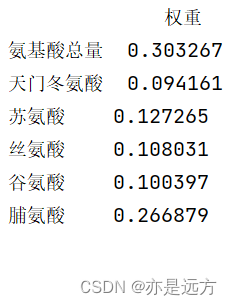
熵值法求权重
Hands on deep learning pytorch version exercise solution -- implementation of 3-2 linear regression from scratch
20220607其他:两整数之和
Ut2016 learning notes
LeetCode - 715. Range module (TreeSet)*****
LeetCode - 900. RLE iterator
An open source OA office automation system
20220531数学:快乐数
I really want to be a girl. The first step of programming is to wear women's clothes
20220606 Mathematics: fraction to decimal
[C question set] of Ⅵ
七、MySQL之数据定义语言(二)
Leetcode刷题---1385
High imitation bosom friend manke comic app
Leetcode - 705 design hash set (Design)
What useful materials have I learned from when installing QT
Timo background management system