粒子滤波 PF——在机动目标跟踪中的应用（粒子滤波VS扩展卡尔曼滤波）

对于该博客跟踪代码以及问题探讨可以联系：WX：ZB823618313
对于其他跟踪定位问题的代码及探讨也可以联系

原创不易，路过的各位大佬请点个赞

一、问题描述（离散时间非线性系统描述）

考虑一般非线性系统模型，
$$\begin{gathered} x_k=f(x_{k-1},w_{k-1}) \\ {z}_k=h(x_k,v_k)\text{\hspace{1em}(1)} \end{gathered}$$
其中$x_k$为$k$时刻的目标状态向量。$z_k$为$k$时刻量测向量（传感器数据）。这里不考虑控制器$u_k$。$w_k$和$v_k$分别是过程噪声序列和量测噪声序列，并假设$w_k$和$v_k$为零均值高斯白噪声，其方差分别为$Q_k$和$R_k$的高斯白噪声，即$w_k\sim (0,Q_k)$, $v_k\sim (0,R_k)$，且满足如下关系(线性高斯假设)为：
$$\begin{array}{rl}E[w_i{v}_j^{\prime }]& =0\\ E[w_i{w}_j^{\prime }]& =0i\ne j\\ E[v_i{v}_j^{\prime }]& =0i\ne j\end{array}$$

二、粒子滤波 PF

核心思想：是使用一组具有相应权值的随机样本(粒子)来表示状态的后验分布。该方法的基本思路是选取一个重要性概率密度并从中进行随机抽样，得到一些带有相应权值的随机样本后，在状态观测的基础上调节权值的大小。和粒子的位置，再使用这些样本来逼近状态后验分布，最后将这组样本的加权求和作为状态的估计值。粒子滤波不受系统模型的线性和高斯假设约束，采用样本形式而不是函数形式对状态概率密度进行描述，使其不需要对状态变量的概率分布进行过多的约束，因而在非线性非高斯动态系统中广泛应用。尽管如此，粒子滤波目前仍存在计算量过大、粒子退化等关键问题亟待突破。

通常情况下选择先验分布作为重要性密度函数、即
$$q(x_k|x_{k-1}^{(i)},z_k)=p(x_k|x_{k-1}^{(i)})$$
对该函数取重要性权值为
$$w_k^{(i)}=w_{k-1}^{(i)}p(z_k|x_k^{(i)})$$
同样$w_k^{(i)}$需要归一化得到${\tilde{w}}_k^{(i)}$。

标准的粒子滤波算法步骤为：

粒子滤波PF:
Step 1: 根据$p(x_0)$采样得到$N$个粒子 $x_0^{(i)}\sim p(x_0)$
For $i=2:N$
  Step 2: 根据状态转移函数产生新的粒子为：$$$x_k^{(i)}\sim p(x_k|x_{k-1}^{(i)})$$
  Step 3: 计算重要性权值：$$w_k^{(i)}=w_{k-1}^{(i)}p(z_k|x_k^{(i)})$$
  Step 4: 归一化重要性权值：$${\tilde{w}}_k^{(i)}=\frac{w_k^{(i)}}{{\sum }_{j=1}^N{w}_k^{(j)}}$$
  Step 5: 使用重采样方法对粒子进行重采样（以系统重采样为例）
  Step 6: 得到$k$时刻的后验状态估计：
$$E[{\hat{x}}_k]=\sum _{i=1}^N{x}_k^{(i)}{\tilde{w}}_k^{(i)}$$
End For

粒子滤波PF算法结构图

算法：系统重采样 （systematic resampling）
For $i=1:N$
  Step 1: 初始化累积概率密度函数CDF：$c_1=0$
For $i=2:N$
  Step 2: 构造CDF: $c_i=c_{i-1}+w_k^{(i)}$
  Step 3: 从CDF的底部开始：$i=1$
  Step 4: 采样起始点：$u_1=\mathcal{U}[0,1/N]$
End For
For $j=1:N$
  Step 5: 沿CDF移动: $u_j=u_1+(j-1)/N$
  Step 6: While $u_j>c_i$
      $i=i+1$
     End While
  Step 7: 赋值粒子：$x_k^{(j)}=x_k^{(i)}$
  Step 8: 赋值权值：$w_k^{(j)}=1/N$
  Step 9: 赋值父代：$i^{(j)}=i$
End For

三、仿真场景：三维雷达目标跟踪

3.1 仿真场景（三维螺旋上升机动目标）

目标模型
考虑一各三维的匀速转弯运动目标：
$$x_{k+1}=F_k{x}_k+G_k{w}_k$$
其中状态向量$x_k=[x_k,{\dot{x}}_k,y_k,{\dot{y}}_k,z_k,{\dot{z}}_k{]}^{\prime }$；噪声为$w_k=[w_x,w_y,w_z{]}^{\prime }$；

目标运动轨迹为三维匀速转弯运动模型
运动轨迹：螺旋上升

如果为非线性目标，则将状态转移矩阵$F_k$代替为雅可比矩阵即可。为了不是一般性这里采用线性模型进行仿真。主要处理目标跟踪，雷达量测存在的非线性滤波问题。

雷达量测模型
在三维情况下，雷达量测为距离和角度
$$\begin{gathered} r_k^m=r_k+{\tilde{r}}_k \\ {b}_k^m=b_k+{\tilde{b}}_k \\ {e}_k^m=e_k+{\tilde{e}}_k \end{gathered}$$
其中
$$\begin{gathered} r_k=\sqrt{(x_k-x_0{)}^{+}(y_k-y_0{)}^2)} \\ {b}_k={\tan }^{-1}\frac{y_k-y_0}{x_k-x_0} \\ {e}_k={\tan }^{-1}\frac{z_k-z_0}{\sqrt{(x_k-x_0{)}^2+(y_k-y_0{)}^2}} \end{gathered}$$
$[x_0,y_0,z_0]$为雷达坐标，一般情况为0。雷达量测为$z_k=[r_k,b_k,e_k{]}^{\prime }$。雷达量测方差为
$$R_k=\text{cov}(v_k)=\left[\begin{array}{ccc}{\sigma }_r^2& 0& 0\\ 0& {\sigma }_b^2& 0\\ 0& 0& {\sigma }_e^2\end{array}\right]$$且${\sigma }_r=20m$， ${\sigma }_b=20mrad$, ${\sigma }_e=15mrad$。
性能指标
RMSE(Root mean-squared error):蒙塔卡罗次数$M=500$，${\hat{x}}_{k|k}^i$为第$i$次仿真得到的估计。
$$\text{RMSE}(\hat{x})=\sqrt{\frac{1}{M}\sum _{i=1}^M({\mathbf{x}}_k-{\hat{\mathbf{x}}}_{k|k}^i)({\mathbf{x}}_k-{\hat{\mathbf{x}}}_{k|k}^i{)}^{\prime }}$$
$$\text{Position RMSE}(\hat{x})=\sqrt{\frac{1}{M}\sum _{i=1}^M(x_k-{\hat{x}}_{k|k}^i{)}^2+(y_k-{\hat{y}}_{k|k}^i{)}^2+(z_k-{\hat{z}}_{k|k}^i{)}^2}$$
$$\text{Velocity RMSE}(\hat{x})=\sqrt{\frac{1}{M}\sum _{i=1}^M({\dot{x}}_k-{\hat{\dot{x}}}_{k|k}^i{)}^2+({\dot{y}}_k-{\hat{\dot{y}}}_{k|k}^i{)}^2+({\dot{z}}_k-{\hat{\dot{z}}}_{k|k}^i{)}^2}$$
ANEES（average normalized estimation error square）,$n$ 为状态维数，${\mathbf{P}}_{k|k}^i$为第$i$次仿真滤波器输出的估计协方差
$$\text{ANEES}(\hat{x})=\frac{1}{Mn}\sum _{i=1}^M({\mathbf{x}}_k-{\hat{\mathbf{x}}}_{k|k}^i{)}^{\prime }({\mathbf{P}}_{k|k}^i{)}^{-1}({\mathbf{x}}_k-{\hat{\mathbf{x}}}_{k|k}^i)$$

3.2 跟踪轨迹

三维跟踪轨迹：

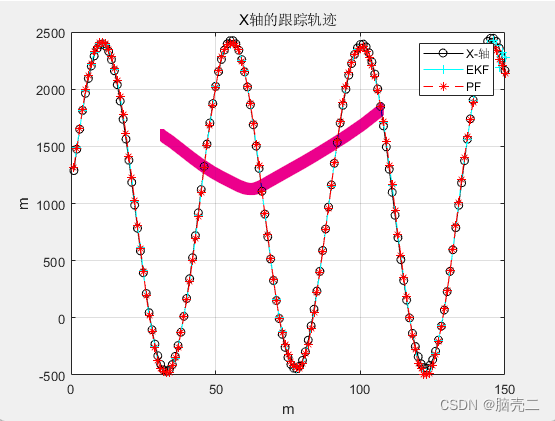
3.3 跟踪误差

四、部分代码

对于该博客跟踪代码以及问题探讨可以联系：WX：ZB823618313
对于其他跟踪定位问题的代码及探讨也可以联系

代码：系统重采样 （systematic resampling）

%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% 系统重采样子函数
% 输入参数：weight为原始数据对应的权重大小
% 输出参数：outIndex是根据weight筛选和复制结果
function outIndex = systematicR(weight);
N=length(weight);
N_children=zeros(1,N);
label=zeros(1,N);
label=1:1:N;
s=1/N;
auxw=0;
auxl=0;
li=0;
T=s*rand(1);
j=1;
Q=0;
i=0;
u=rand(1,N);
while (T<1)
    if (Q>T)
        T=T+s;
        N_children(1,li)=N_children(1,li)+1;
    else
        i=fix((N-j+1)*u(1,j))+j;
        auxw=weight(1,i);
        li=label(1,i);
        Q=Q+auxw;
        weight(1,i)=weight(1,j);
        label(1,i)=label(1,j);
        j=j+1;
    end
end
index=1;
for i=1:N
    if (N_children(1,i)>0)
        for j=index:index+N_children(1,i)-1
            outIndex(j) = i;
        end;
    end;
    index= index+N_children(1,i);
end
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%