当前位置:网站首页>Leetcode(347)——前 K 个高频元素
Leetcode(347)——前 K 个高频元素
2022-07-05 20:09:00 【SmileGuy17】
Leetcode(347)——前 K 个高频元素
题目
题解
方法一:桶排序
思路
顾名思义,桶排序的意思是为每个值设立一个桶,桶内记录这个值出现的次数(或其它属性),然后对桶进行排序。针对样例来说,我们先通过桶排序得到三个桶 [1,2,3,4],它们的值分别为 [4,2,1,1],表示每个数字出现的次数。
紧接着,我们对桶的频次进行排序,前 k 大个桶即是前 k 个频繁的数。这里我们可以使用各种排序算法,甚至可以再进行一次桶排序,把每个旧桶根据频次放在不同的新桶内。针对样例来说,因为目前最大的频次是 4,我们建立 [1,2,3,4] 四个新桶,它们分别放入的旧桶为 [[3,4],[2],[],[1]],表示不同数字出现的频率。最后,我们从后往前遍历,直到找到 k 个旧桶。
代码实现
我的:
class Solution {
public:
vector<int> topKFrequent(vector<int>& nums, int k) {
if(nums.size() == 1) return nums;
unordered_map<int, int> times;
int maxcount = 0;
for(auto& it: nums) maxcount = max(maxcount, ++times[it]);
vector<vector<int>> bucket(maxcount+1);
for(auto& it: times) bucket[it.second].push_back(it.first);
vector<int> ans;
// 因为保证答案唯一,所以不考虑 maxcount 的大小
while(k > 0){
if(!bucket[maxcount].empty()){
k -= bucket[maxcount].size();
ans.insert(ans.end(), bucket[maxcount].begin(), bucket[maxcount].end());
}
maxcount--;
}
return ans;
}
};
复杂度分析
时间复杂度: O ( n ) O(n) O(n),其中 n n n 是数组长度
空间复杂度: O ( m a x ( n , k ) ) O(max(n, k)) O(max(n,k)),其中 n n n 是数组长度
方法二:堆排序
思路
首先遍历整个数组,并使用哈希表记录每个数字出现的次数,并形成一个「出现次数数组」。找出原数组的前 k k k 个高频元素,就相当于找出「出现次数数组」的前 k k k 大的值。
最简单的做法是给「出现次数数组」排序。但由于可能有 O ( N ) O(N) O(N) 个不同的出现次数(其中 N N N 为原数组长度),故总的算法复杂度会达到 O ( N log N ) O(N\log N) O(NlogN),不满足题目的要求。
在这里,我们可以利用堆的思想:建立一个小顶堆,然后遍历「出现次数数组」:
- 如果堆的元素个数小于 k k k,就可以直接插入堆中。
- 如果堆的元素个数等于 k k k,则检查堆顶与当前出现次数的大小。如果堆顶更大,说明至少有 k k k 个数字的出现次数比当前值大,故舍弃当前值;否则,就弹出堆顶,并将当前值插入堆中。
遍历完成后,堆中的元素就代表了「出现次数数组」中前 k k k 大的值。
代码实现
Leetcode 官方题解:
class Solution {
public:
static bool cmp(pair<int, int>& m, pair<int, int>& n) {
return m.second > n.second;
}
vector<int> topKFrequent(vector<int>& nums, int k) {
unordered_map<int, int> occurrences;
for (auto& v : nums) {
occurrences[v]++;
}
// pair 的第一个元素代表数组的值,第二个元素代表了该值出现的次数
priority_queue<pair<int, int>, vector<pair<int, int>>, decltype(&cmp)> q(cmp);
for (auto& [num, count] : occurrences) {
if (q.size() == k) {
if (q.top().second < count) {
q.pop();
q.emplace(num, count);
}
} else {
q.emplace(num, count);
}
}
vector<int> ret;
while (!q.empty()) {
ret.emplace_back(q.top().first);
q.pop();
}
return ret;
}
};
复杂度分析
时间复杂度: O ( N log k ) O(N\log k) O(Nlogk),其中 N N N 为数组的长度。我们首先遍历原数组,并使用哈希表记录出现次数,每个元素需要 O ( 1 ) O(1) O(1) 的时间,共需 O ( N ) O(N) O(N) 的时间。随后,我们遍历「出现次数数组」,由于堆的大小至多为 k k k,因此每次堆操作需要 O ( log k ) O(\log k) O(logk) 的时间,共需 O ( N log k ) O(N\log k) O(Nlogk) 的时间。二者之和为 O ( N log k ) O(N\log k) O(Nlogk)。
空间复杂度: O ( N ) O(N) O(N)。哈希表的大小为 O ( N ) O(N) O(N),而堆的大小为 O ( k ) O(k) O(k),共计为 O ( N ) O(N) O(N)。
方法三:(改进的)快速排序——即快速选择排序
思路
我们可以使用快速选择算法,求出「出现次数数组」的前 k k k 大的值。
首先我们使用 arr \textit{arr} arr 数组存储每个数字对应的出现次数,然后遍历数组获取出现次数。然后对 arr \textit{arr} arr 数组进行快速排序。
在对数组 arr [ l … r ] \textit{arr}[l \ldots r] arr[l…r] 做快速排序的过程中,我们首先将数组划分为两个部分 arr [ i … q − 1 ] \textit{arr}[i \ldots q-1] arr[i…q−1] 与 arr [ q + 1 … j ] \textit{arr}[q+1 \ldots j] arr[q+1…j],并使得 arr [ i … q − 1 ] \textit{arr}[i \ldots q-1] arr[i…q−1] 中的每一个值都不超过 arr [ q ] \textit{arr}[q] arr[q],且 arr [ q + 1 … j ] \textit{arr}[q+1 \ldots j] arr[q+1…j] 中的每一个值都大于 arr [ q ] \textit{arr}[q] arr[q]。
于是,我们根据 k k k 与左侧子数组 arr [ i … q − 1 ] \textit{arr}[i \ldots q-1] arr[i…q−1] 的长度(为 q − i q q-iq q−iq)的大小关系:
- 如果 k ≤ q − i k \le q-i k≤q−i,则数组 arr [ l … r ] \textit{arr}[l \ldots r] arr[l…r] 前 k k k 大的值,就等于子数组 arr [ i … q − 1 ] \textit{arr}[i \ldots q-1] arr[i…q−1] 前 k k k 大的值。
- 否则,数组 arr [ l … r ] \textit{arr}[l \ldots r] arr[l…r] 前 k k k 大的值,就等于左侧子数组全部元素,加上右侧子数组 arr [ q + 1 … j ] \textit{arr}[q+1 \ldots j] arr[q+1…j] 中前 k − ( q − i ) k - (q - i) k−(q−i) 大的值。
原版的快速排序算法的平均时间复杂度为 O ( N log N ) O(N\log N) O(NlogN)。我们的算法中,每次只需在其中的一个分支递归即可,因此算法的平均时间复杂度降为 O ( N ) O(N) O(N)。
代码实现
Leetcode 官方题解:
class Solution {
public:
void qsort(vector<pair<int, int>>& v, int start, int end, vector<int>& ret, int k) {
int picked = rand() % (end - start + 1) + start;
swap(v[picked], v[start]);
int pivot = v[start].second;
int index = start;
for (int i = start + 1; i <= end; i++) {
if (v[i].second >= pivot) {
swap(v[index + 1], v[i]);
index++;
}
}
swap(v[start], v[index]);
if (k <= index - start) {
qsort(v, start, index - 1, ret, k);
} else {
for (int i = start; i <= index; i++) {
ret.push_back(v[i].first);
}
if (k > index - start + 1) {
qsort(v, index + 1, end, ret, k - (index - start + 1));
}
}
}
vector<int> topKFrequent(vector<int>& nums, int k) {
unordered_map<int, int> occurrences;
for (auto& v: nums) {
occurrences[v]++;
}
vector<pair<int, int>> values;
for (auto& kv: occurrences) {
values.push_back(kv);
}
vector<int> ret;
qsort(values, 0, values.size() - 1, ret, k);
return ret;
}
};
复杂度分析
时间复杂度:
其中 N N N 为数组的长度。设处理长度为 N N N 的数组的时间复杂度为 f ( N ) f(N) f(N)。由于处理的过程包括一次遍历和一次子分支的递归,最好情况下,有 f ( N ) = O ( N ) + f ( N / 2 ) f(N) = O(N) + f(N/2) f(N)=O(N)+f(N/2),根据主定理,能够得到 f ( N ) = O ( N ) f(N) = O(N) f(N)=O(N)。
最坏情况下,每次取的枢轴都位于数组的两端,时间复杂度退化为 O ( N 2 ) O(N^2) O(N2)。但由于我们在每次递归的开始会先随机选取中枢元素,故出现最坏情况的概率很低。
平均情况下,时间复杂度为 O ( N ) O(N) O(N)。
空间复杂度: O ( N ) O(N) O(N)。其中哈希表的大小为 O ( N ) O(N) O(N),用于排序的辅助数组的大小也为 O ( N ) O(N) O(N),快速排序的空间复杂度最好情况为 O ( log N ) O(\log N) O(logN),最坏情况为 O ( N ) O(N) O(N)
边栏推荐
- 1: Citation;
- 关于BRAM IP复位的优先级
- 【数字IC验证快速入门】7、验证岗位中必备的数字电路基础知识(含常见面试题)
- 深度学习 卷积神经网络(CNN)基础
- 多分支结构
- third-party dynamic library (libcudnn.so) that Paddle depends on is not configured correctl
- Concept and syntax of function
- leetcode刷题:二叉树10(完全二叉树的节点个数)
- Leetcode skimming: binary tree 17 (construct binary tree from middle order and post order traversal sequence)
- JS implementation prohibits web page zooming (ctrl+ mouse, +, - zooming effective pro test)
猜你喜欢
Leetcode skimming: binary tree 17 (construct binary tree from middle order and post order traversal sequence)
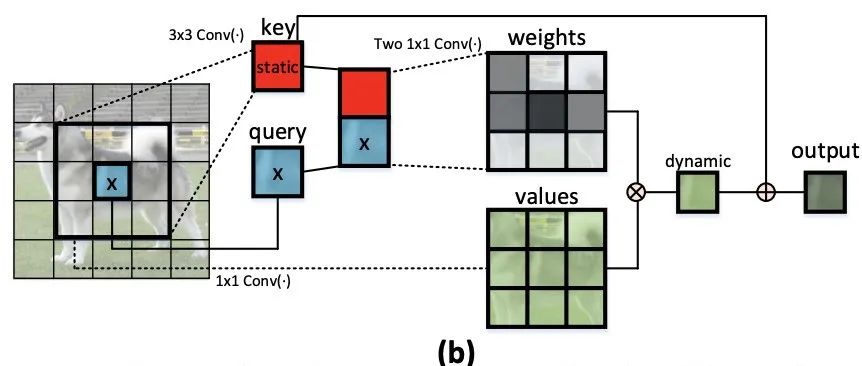
无卷积骨干网络:金字塔Transformer,提升目标检测/分割等任务精度(附源代码)...
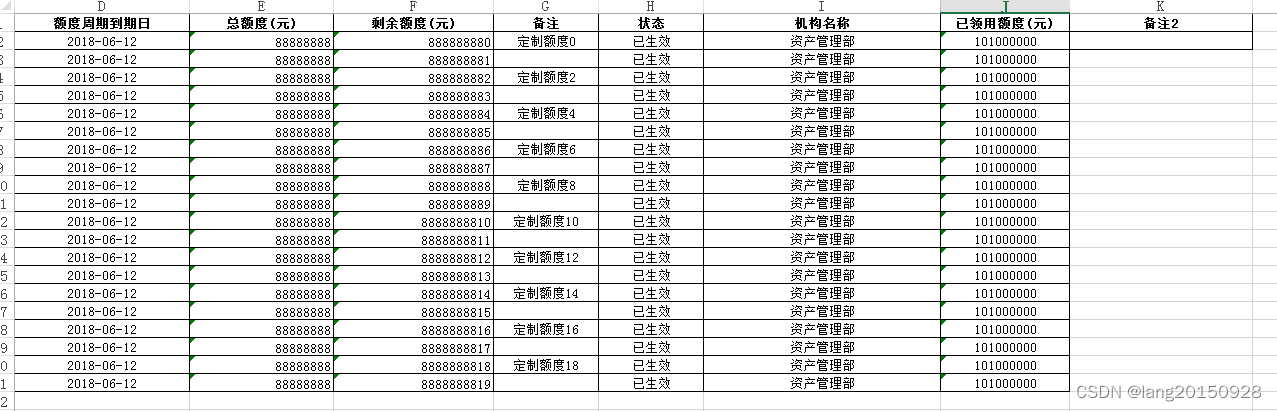
Two pits exported using easyexcel template (map empty data columns are disordered and nested objects are not supported)
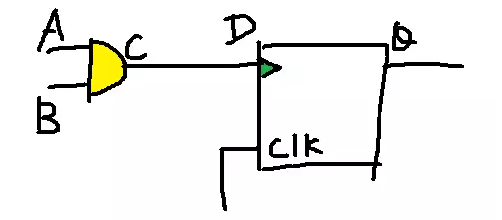
IC科普文:ECO的那些事儿
Redis cluster simulated message queue

浅浅的谈一下ThreadLocalInsecureRandom
Database logic processing function
【数字IC验证快速入门】2、通过一个SoC项目实例,了解SoC的架构,初探数字系统设计流程
ACM getting started Day1
Jvmrandom cannot set seeds | problem tracing | source code tracing
随机推荐
Debezium series: idea integrates lexical and grammatical analysis ANTLR, and check the DDL, DML and other statements supported by debezium
【数字IC验证快速入门】7、验证岗位中必备的数字电路基础知识(含常见面试题)
[C language] merge sort
Ffplay document [easy to understand]
C langue OJ obtenir PE, ACM démarrer OJ
浅浅的谈一下ThreadLocalInsecureRandom
95后阿里P7晒出工资单:狠补了这个,真香...
如何安全快速地从 Centos迁移到openEuler
Securerandom things | true and false random numbers
国信证券在网上开户安全吗?
浮动元素与父级、兄弟盒子的关系
2022年7月4日-2022年7月10日(ue4视频教程mysql)
ByteDance dev better technology salon was successfully held, and we joined hands with Huatai to share our experience in improving the efficiency of web research and development
- Oui. Net Distributed Transaction and Landing Solution
sun.misc.BASE64Encoder报错解决方法[通俗易懂]
Two pits exported using easyexcel template (map empty data columns are disordered and nested objects are not supported)
14. Users, groups, and permissions (14)
Go language | 03 array, pointer, slice usage
leetcode刷题:二叉树16(路径总和)
Flume series: interceptor filtering data