当前位置:网站首页>Matlab learning notes
Matlab learning notes
2022-07-07 00:27:00 【Evergreen AAS】
notes :
- Although the documentation is comprehensive , But this article is mainly to speed up in one day , So please forgive me for my shortcomings .
- The code is based on vscode/py 3.6 Called matlab terminal
Basic mathematical operations and matrix operations
Basic grammar
Variable
- No declaration required
- use = Assign a value to a variable
Variable name
- Variable names are case sensitive ( I don't know if it's because windows Why
- Variable names can only be used by [
0~9,a~z,A~z,_] form , And the variable name cannot start with a number . - Reserved variables are not suitable for variable names
- Use
iskeywordCommand can view program keywords , These keywords are not allowed to be used as variable names .
- Use
Variable | significance |
|---|---|
ans | The result of the last sentence |
i,j | Complex operator ,( We need to pay attention here ) |
Inf | infinite |
eps | Floating point relative precision , namely 1.0 The distance to the next floating-point number ( The value is 2.2204e-16) |
NaN | The digital |
pi | PI |
Variable names should not override built-in function names
stay MATLAB in , Call priority of variables (calling priority) Higher than function , Therefore, variable names should not override built-in functions .
for example :
cos = 'changqingaas'; cos(8) % disp(['ans is ', num2str(ans)]) clear; % If a function is overwritten by a variable name , Call clear < Variable name > You can unbind the variable name on the function name cos(8) % disp(['ans is ', num2str(ans)])
notes :clear It's a dangerous order , Because if you do not add parameters after this command , It means to clear all variables in the current workspace .
Output :
ans =
'n'
ans =
-0.1455Variable type
logical,char,numeric,cell,struct And the array or matrix composed of them .
Display format of numeric variables
Numeric variables , Default to double Stored in form .
Can pass format < Display format > Change the display format of numeric variables .
MATLAB Command line
- Use end of line
;Suppress output :- Use after a line of command
;Suppress output , Otherwise, the calculation result will be displayed on the terminal .
- Use after a line of command
- | command | effect | Running results | | ———- | —————————————————————————————— | —————————————————————————————— | |
clc| Clear the output of the terminal | | |clear| By default, all variables in the current workspace are cleared | | |who| Display all variables in the workspace in a simplified format | Your variable is : ans | |whos| Display all variables in the workspace in a complex format | Name Size Bytes Class Attributes ans 1x1 8 double | | which | Check the location of the built-in function source code file , AndeditCommand can be combined to view the source code of built-in functions . | |
Use MATLAB Do numerical calculations
Use MATLAB Calculate mathematical expressions
- After the mathematical expression is calculated , Its value is stored in the variable ans
- log Express ln
- exp(x) Express e^x
MATLAB Built in mathematical functions
- MATLAB Built in arithmetic operation function
- Basic operation :
- Add :
+,sum,cumsum,movsum - reduce :
-,diff - ride :
.*,*,prod,cumprod - except :
./,.\,/,\ - chengfang :
.^,^
- Add :
- Modulus operation :
mod,rem,idivide,ceil,fix,floor,round
- Basic operation :
- MATLAB Built in trigonometric function
- sine : sin,sind,sinpi,asin,asind,sinh,asinh
- cosine : cos,cosd,cospi,acos,acosd,cosh,acosh
- tangent : tan,tand,atan,atand,atan2,atan2d,tanh,atanh
- Cosecant : csc,cscd,acsc,acscd,csch,acsch
- Secant : sec,secd,asec,asecd,sech,asech
- Cotangent : cot,cotd,acot,acotd,coth,acoth
- hypotenuse : hypot
- transformation : deg2rad,rad2deg,cart2pol,cart2sph,pol2cart,sph2cart
- MATLAB Built in exponential logarithmic function :
- exp,expm1,log,log10,log1p,log2,nextpow2,nthroot,pow2,reallog,realpow,realsqrt,sqr
- MATLAB Built in complex function :
- abs,angle,complex,conj,cplxpair,i,imag,isreal,j,real,sign,unwrap
Use MATLAB Do matrix operations
Define the matrix
Input the matrix to the terminal
stay MATLAB in , Use [] Enclose the matrix contents to be input , Use spaces or commas , Separate inline variables , Use ; Separate each line .
Use the colon operator to create a vector
Use the colon operator : You can create a long vector , The syntax is as follows :
for example :
Define a special matrix
command | The result |
|---|---|
eye(n) | Get one n × n The identity matrix of |
zeros(n1, n2) | Get one n1 × n2 Of all the 0 matrix |
ones(n1, n2) | Get one n1 × n2 Of all the 1 matrix |
diag(vector) | Get a vector vector The content in is the diagonal matrix of diagonal |
The index of the matrix
- MATLAB The matrix in is represented by Column Sequentially stored . And the index subscript is from 1 Start .
- Matrices can be indexed in two ways : Index by one dimension and index by two dimensions . For a general matrix , The index order is as follows : \begin{bmatrix} 1 or (1,1) & 4 or (1,2) & 7 or (1,3) \\ 2 or (2,1) & 5 or (2,2) & 8 or (2,3) \\ 3 or (3,1) & 6 or (3,2) &9 or (3,3) \end{bmatrix}
- The index of matrix can use colon
:, Means to select all rows or columns . - The index of a matrix can be one or two vectors , Indicates that all rows or columns in the selected vector . | Primitive matrix | Indexes | The result || —————————————————————————————— | ———————- | ———————————————————————————- || \begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6\\ 7 & 8 & 9 \end{bmatrix}\begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6\\ 7 & 8 & 9 \end{bmatrix}\begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6\\ 7 & 8 & 9 \end{bmatrix}\begin{bmatrix} 1 & 4 \\ 7 & 2\end{bmatrix}\begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6\\ 7 & 8 & 9 \end{bmatrix}\begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6\\ 7 & 8 & 9 \end{bmatrix}\begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6 \end{bmatrix}\begin{bmatrix} 1 & 2 & 3 \\ 4 & 5 & 6\\ 7 & 8 & 9 \end{bmatrix}\begin{bmatrix} 1 & 2 \\ 7 & 8 \end{bmatrix}
Matrix operations
Operator of operation matrix
Operator | operation | form | Example |
|---|---|---|---|
+ | Add matrix and vector | A+b | [6 3] + 2 = [8 5] |
- | Matrix subtracts from vector | A-b | [6 3] - 2 = [4 1] |
+ | Add the matrix to its corresponding position | A+B | [6 3] + [4 8] = [10 11] |
- | The matrix is subtracted from the corresponding position of the matrix | A-B | [6 3] - [4 8] = [2 -5] |
* | Matrix Matrix Multiplication | A*B | [6 3] * [4 8]' = 48 |
.* | Multiply the matrix by its corresponding position | A.*B | [6 3] * [4 8] = [24 24] |
/ | Matrix and matrix right division ( Equivalent to A*inv(B)) | A/B | [6 3] / [4 8] = 0.6 |
\ | Matrix and matrix left division ( Equivalent to inv(A)*B) | A\B | [6 3] / [4 8] = [0.06667 1.3333; 0 0] |
./ | The matrix and the corresponding position of the matrix are divided by | A./B | [6 3] ./ [4 8] = [1.5 0.375] |
.\ | The matrix and the corresponding position of the matrix are divided by left | A.\B | [6 3] .\ [4 8] = [0.6667 2.6667] |
^ | Matrix and vector power | A^b | [1 2; 3 4]^3 = [37 54; 81 118] |
.^ | Matrix and matrix corresponding position power | A.^B | [1 2; 3 4].^[1 2; 3 4] = [1 4; 27 256] |
Function of operation matrix
For the following matrix
A=\begin{bmatrix} 1 & 2 & 3 \\ 0 & 5 & 6 \\ 7 & 0 & 9 \end{bmatrix}
Operate to demonstrate common functions of the operation matrix
For the above functions , Except for the first parameter , Other parameters are optional .
Structured programming and function definition
Structured programming
Process control statements and logical operators
Flow control statement | effect |
|---|---|
if, elseif, else | if if The statement is true , Execute clause |
switch, case, otherwise | according to switch The content of the statement determines which clause to execute |
while | Repeat the clause until while The condition in is false |
for | Execute the clause a fixed number of times |
try, catch | Execute clauses and catch exceptions during execution |
break | Out of the loop |
continue | Go directly to the next cycle |
end | End clause |
pause | Suspend program |
return | Return to the calling function |
All the above loops and conditional statements should end with end closed .
MATLAB There are also the following logical operators :
Operator | significance | ||
|---|---|---|---|
== | be equal to | ||
~= | It's not equal to | ||
&& | And ( Support logic short circuit ) | ||
` | ` | or ( Support logic short circuit ) |
Example of process control statement
if sentence :
if condition1 statement1 elseif condition2 statement2 else statement3 end
switch sentence
switch expression
case value1
statement1
case value2
statement2
otherwise
statement
endwhile sentence
while expression statement end
for sentence
for variable = start:increment:end commands end
break sentence
x = 2; k = 0; error = inf;
error_threshold = 1e-32;
while error > error_threshold
if k > 100
break
end
x = x - sin(x) / cos(x);
error = abs(x - pi);
k = k + 1;
endTry to pre allocate memory space when using circular statements
Problems that should be paid attention to when writing scripts
Add a statement at the beginning of the script to empty the workspace
At the beginning of each script , The following statement should be added , Clear the workspace cache and traces of previous program runs :
clear all % Clear variables in the workspace memory close all % Close the image drawn by the program before clc % Clear the output of the program on the terminal before
Semicolons should be added after operations and assignment statements ; Suppress output
Semicolons should be added to all operations and assignment statements ; Suppress output , If you need to output a variable to the terminal , It should be called disp Method .
Use ellipsis ... Splice multiple lines
stay MATLAB in , Ellipsis ... You can splice multiple lines of statements into one line , Using this statement flexibly can improve the readability of the code .
function
Similar to scripts , Functions can be stored Function name .m In file , It can also be defined in memory in the form of a function handle .
See built-in functions
We can use which Command to view the location of the built-in function source code file , And edit Command can be combined to view the source code of built-in functions .
Run the following statement to open MATLAB Built in mean Function source file :
edit(which('mean.m')) With Function name .m File form definition function
stay MATLAB The format of the function defined in the file is as follows :
function [ Output variable name ] = Function name ( Enter variable name ) % Documentation for functions function code
functionIt's a keyword , Declare that what is saved in this file is a function .The input variableandOutput variablesnonessential , Functions can have no input variables , You can also have no output variables .Function nameShould and.mSame file name , And does not contain special characters ( It's better not to have Chinese ).
MATLAB Built in function parameters
Function parameter | significance |
|---|---|
imputname | Enter a list of variable names |
mfilename | Function source code file name |
nargin | Enter the number of variables |
nargout | Number of output variables |
varargin | Variable length input parameter list |
varargout | Variable length output parameter list |
MATLAB It does not provide the syntax of specifying default parameter values and function overloading in other high-level languages , But use the built-in function parameters mentioned above flexibly , You can specify the default parameter value and method overloading to a certain extent :
MATLAB Function definition example 1
The surface program is used to calculate the displacement of a free falling body :x = x_{0} + v_{0}t + \frac{1}{2} g t^2
function x = freebody(x0,v0,t) % calculation of free falling % x0: initial displacement in m % v0: initial velocity in m/sec % t: the elapsed time in sec % x: the depth of falling in m x = x0 + v0.*t + 1/2*9.8*t.*t;
This function demonstrates a MATLAB Programming skills : Try to use .* Instead of *, Because the former is not only for parameters t Scalar case is available , Also for variables t In the case of vectors or matrices .
freebody(0, 0, 2) % obtain 19.6000 freebody(0, 0, [0 1 2 3]) % obtain [0 4.9000 19.6000 44.1000] freebody(0, 0, [0 1; 2 3]) % obtain [0 4.9000; 19.6000 44.1000]
MATLAB Function definition example 2
The following function realizes the conversion from Fahrenheit temperature to Celsius temperature , This function can identify the number of input samples to be converted , When the number of samples to be converted is 0 when , Exit function .
function F2C()
while 1
F_degree = input('tempreature in Fahrenheit: ', 's');
F_degree = str2num(F_degree);
if isempty(F_degree)
return
end
C_degree = (F_degree-32)*5/9;
disp(['tempreature in Celsius: ' num2str(C_degree)])
endDefine a function in the form of a function handle
We can also define functions in the form of function handles , This is closer to the mathematical definition of function , The syntax is as follows :
Function handle = @( The input variable ) Output variables
You can call this method directly through the function handle .
f = @(x) exp(-2*x); x = 0:0.1:2; plot(x, f(x));
Data type and file reading and writing
data type
MATLAB The main data types in are as follows :
value type (numeric)
MATLAB The supported value types are shown in the following table :
value type | describe |
|---|---|
double | Double precision floating point |
single | Single-precision floating-point |
int8 | 8 Bit signed integer |
int16 | 16 Bit signed integer |
int32 | 32 Bit signed integer |
int64 | 64 Bit signed integer |
uint8 | 8 Bit unsigned integer |
uint16 | 16 Bit unsigned integer |
uint32 | 32 Bit unsigned integer |
uint64 | 64 Bit unsigned integer |
stay MATLAB in , Variables of numeric type are defaulted to double Type of , You can use type conversion to convert it to other numeric types .
n = 3; class(n) n = int8(3); class(n)
Output :
ans =
'double'
ans =
'int8'String type (char)
stay MATLAB in , The string type consists of a pair of single quotation marks ' Wrap a paragraph of text to define . standard ASCII Characters can be converted to corresponding ASCII code .
s1 = 'h'; uint16(s1) % obtain 104
Strings are stored in memory in the form of a character matrix , You can index the matrix and assign values to it :
str1 = 'hello'; str2 = 'world'; str3 = [str1 str2]; size(str3) % obtain [1 10] str4 = [str1; str2]; size(str4) % obtain [2 5]
str = 'aardvark'; 'a' == str % obtain [1 1 0 0 0 1 0 0] str(str == 'a') = 'Z' % obtain 'ZZrdvZrk'
Structure (structure)
stay MATLAB in , The structure is a key value pair
The basic use of structures
- Similar to most programming languages ,MATLAB Use
.To access the fields in the structure :
student.name = 'John Doe'; student.id = '[email protected]'; student.number = 301073268; student.grade = [100, 75, 73; ... 95, 91, 85.5; ... 100, 98, 72]; student
Using subscript expressions on the structure list can expand or reduce the structure list .
student.name = 'John Doe'; student.id = '[email protected]'; student.number = 301073268; student.grade = [100, 75, 73; 95, 91, 85.5; 100, 98, 72]; student student(2).name = 'Ann Lane'; student(2).id = '[email protected]'; student(2).number = 301078853; student(2).grade = [95 100 90; 95 82 97; 100 85 100]; student(1) = [] % Delete student The first item on the list
Structures can be cascaded , That is, the value of the field in the structure can also be the structure :
A = struct('data', [3 4 7; 8 0 1], ...
'nest', struct('testnum', 'Test 1', ...
'xdata', [4 2 8], ...
'ydata', [7 1 6]));
A(2).data = [9 3 2; 7 6 5];
A(2).nest.testnum = 'Test 2';
A(2).nest.xdata = [3 4 2];
A(2).nest.ydata = [5 0 9];
ACommon functions of structures
function | effect |
|---|---|
struct | Create structure |
struct2cell | Convert the structure to a cell array |
cell2struct | Convert the cell array into a structure |
isstruct | Determine whether a variable is a structure |
structfun | Apply a function to each field of the structure |
fieldnames | Get all field names of the structure |
isfield | Determine whether the structure contains a field |
getfield | Get the value of a field in the structure |
setfield | Assign a value to a field in the structure |
rmfield | Delete a field in the structure |
orderfields | Sort the structure fields |
Cell array (cell)
stay MATLAB in , A cell array is a data structure that can hold different types of elements , Be similar to Python Lists in languages .
Basic use of cellular arrays
Use {} Define a cell array like a matrix :
A = { [1 4 3; 0 5 8; 7 2 9] 'Anne Smith' ;...
3+7i -pi:pi:pi}A(1,1)={[1 4 3; 0 5 8; 7 2 9]};
A(1,2)={'Anne Smith'};
A(2,1)={3+7i};
A(2,2)={-pi:pi:pi};A{1,1}=[1 4 3; 0 5 8; 7 2 9];
A{1,2}='Anne Smith';
A{2,1}=3+7i;
A{2,2}=-pi:pi:pi;
AThe above three methods are equivalent , The second way is to use Cell index assignment , The third way is to use Content index assignment .
- There are two ways to access data in a cellular array , Namely : Cell index
()and Content index{}Because the subset of cell array is still cell array , In the use of indexer content , We need to point out that we are going to visit a Sub cell array still The contents in the corresponding area of the cell array .- Use Cell index
(), What we get is a Sub cell array .- Use Content index
{}, What we get is The contents in the corresponding area of the cell array .
- Use Content index
- Use Cell index
Common functions of cell array
Common functions of cell array
function | effect |
|---|---|
cell | Create a cell array |
iscell | Determine whether a variable is a cellular array |
cell2mat | Turn the cell array into a matrix |
cell2struct | Turn the cell array into a structure |
mat2cell | Converts an array to an array of cells of a specified size |
num2cell | Convert the array to a cell array of the same size |
struct2cell | Convert the structure to a cell array |
celldisp | Recursively display the contents of the cell array |
cellplot | Draw the structure of cell array in image form |
cellfun | Apply a function to each cell of the cell array |
among mat2cell Function can specify the size of each cell in the cell array when converting .
a = magic(3) b = num2cell(a) % obtain % [8] [1] [6] % [3] [5] [7] % [4] [9] [2] c = mat2cell(a, [1 2], [2, 1]) % obtain % [1x2 double] [6] % [2x2 double] [2x1 double]
High dimensional cell array
A three-dimensional cell array can have That's ok (row), Column (column), layer (layer) Three dimensions . When indexing a cell array , The order of priority from high to low is : That's ok → Column → layer .
Use cat Function can splice a cell array on a specified dimension .
A function that determines the data type of a variable
The following functions can judge the type of variables :
function | effect |
|---|---|
isinteger | Judge whether the input parameter is an integer array |
islogical | Judge whether the input parameter is a logical quantity array |
isnumeric | Judge whether the input parameter is a numeric array |
isreal | Judge whether the input parameter is a real array |
ischar | Judge whether the input parameter is a character array |
iscell | Judge whether the input parameter is a cell array |
isfloat | Determine whether the input array is a floating-point array |
ishandle | Determine whether the input array is a valid graphic handle |
isempty | Determine whether the input array is empty |
isprime | Determine which array elements are prime numbers |
isnan | Determine which array elements are NaN |
isinf | Determine which array elements are Inf |
isequal | Determine whether the array is equal |
File read and write
The supported file types are as follows :
The contents of the document | Extension | Function to read the file | Write function to file |
|---|---|---|---|
MATLAB data | *.mat | load | save |
Excel form | *.xls,*.xlsx | xlsread | xlswrite |
Space separated numbers | *.txt | load | save |
Reading and writing MATLAB Formatted data
MATLAB The data in the workspace can be in *.mat The format is saved in a file . Use save Function stores data in a file , Use load Function to read data from a file .
saveThe syntax of the function is as follows :save(filename,variables)Put the variablevariablesStored in a file in binary form .save(filename,variables,'-ascii')Put the variablevariablesSave in text form .
loadThe syntax of the function is as follows :load(filename)Read data from binary form file .load(filename,'-ascii')Read data from a text file .
The parameter filename and variables All in string format , If not specified variables Parameters , Then save all variables in the current workspace into a file .
Complex data formats , Such as
structandcell, Storage in binary format is not supported .
Reading and writing Excel form
Use xlsread and xlswrite Functions can be read and written Excel data , The grammar is as follows :
Read Excel The syntax of the document :[num,txt,raw] = xlsread(filename,sheet,xlRange)
Score = xlsread('04Score.xlsx')
Score = xlsread('04Score.xlsx', 'B2:D4')
[Score Header] = xlsread('04Score.xlsx') write in Excel The grammar of :xlswrite(filename,A,sheet,xlRange)
M = mean(Score);
xlswrite('04Score.xlsx', M, 1, 'E2:E4');
xlswrite('04Score.xlsx', {'Mean'}, 1, 'E1');Basic drawing
Drawing and decoration of drawing lines
Use plot() Function to draw lines
stay MATLAB in , Use plot() Function to draw lines , Its grammar is :
plot(x,y,LineSpec)
LineSpec: Line setting of drawing line , Three designations Linetype , The sign and Color Of Setter Make a string , The setting character does not distinguish the order . For details, please refer to Official documents .
Line symbols | Linetype setter | Mark | Tag setter | Color | Color setter |
|---|---|---|---|---|---|
- | Solid line ( Default ) | o | circle | y | yellow |
-- | Dotted line | plus | m | magenta | |
: | Dotted line | * | asterisk | c | Blue |
-. | Point line | . | spot | r | Red |
x | Cross | g | green | ||
s | square | b | Blue | ||
d | The diamond | w | white | ||
^ | Upper triangle | k | black | ||
v | Lower triangle | ||||
> | Right triangle | ||||
< | Left triangle | ||||
p | Pentagonal | ||||
h | hexagon |
notes :Python Medium matplotlib The way of drawing is almost the same as here
Decorative lines
Use legend() Function to add a legend to the picture
Use legend(label1, ..., labelN) Function can add a legend to the image .
x=0:0.5:4*pi;
y=sin(x); h=cos(x); w=1./(1+exp(-x)); g=(1/(2*pi*2)^0.5).*exp((-1.*(x-2*pi).^2)./(2*2^2));
plot(x,y,'bd-' ,x,h,'gp:',x,w,'ro-' ,x,g,'c^-'); % Draw multiple lines
legend('sin(x)','cos(x)','Sigmoid','Gauss function'); % Add legend Use title() and *label() Add titles and labels to the pictures
x = 0:0.1:2*pi; y1 = sin(x); y2 = exp(-x);
plot(x, y1, '--*', x, y2, ':o');
xlabel('t = 0 to 2\pi');
ylabel('values of sin(t) and e^{-x}')
title('Function Plots of sin(t) and e^{-x}');
legend('sin(t)','e^{-x}'); Use text() and annotation() Add notes to the picture
x = linspace(0,3); y = x.^2.*sin(x); plot(x,y);
line([2,2],[0,2^2*sin(2)]);
str = '$$ \int_{0}^{2} x^2\sin(x) dx $$';
text(0.25,2.5,str,'Interpreter','latex');
annotation('arrow','X',[0.32,0.5],'Y',[0.6,0.4]); Control the axis , Borders and grids
command | effect |
|---|---|
grid on/off | Set mesh visibility |
box on/off | Set border visibility |
axis on/off | Set axis visibility |
axis normal | Restore default behavior , Set the properties of frame aspect ratio mode and data aspect ratio mode to automatic |
axis square | Use coordinate axes of the same length , Adjust the increment between data units accordingly |
axis equal | Use the same data unit length along each axis |
axis tight | Set the coordinate axis range equal to the data range , Make the axis frame closely around the data |
The following example demonstrates axis Effect of command :
t = 0:0.1:2*pi; x = 3*cos(t); y = sin(t); subplot(2, 2, 1); plot(x, y); axis normal subplot(2, 2, 2); plot(x, y); axis square subplot(2, 2, 3); plot(x, y); axis equal subplot(2, 2, 4); plot(x, y); axis equal tight
Draw multiple lines
Draw multiple lines on an image
By default , Every time you execute plot() Function will clear the result of the last drawing , Multiple execution plot() Only the last drawing will be retained .
We can use hold on and hold off The command controls the refresh of the drawing area , Make multiple drawing results remain in the drawing area at the same time .
hold on % Bring up the brush , Start drawing a set of pictures plot(cos(0:pi/20:2*pi)); plot(sin(0:pi/20:2*pi)); hold off % Put down the paintbrush , This group of pictures has been drawn
Draw multiple images in one window
subplot
Operation of graphic objects
stay MATLAB in , Graphics are stored in memory in the form of objects , You can operate on it by getting its graphic handle .
Get graph handle
A graph handle is essentially a floating point number , You can uniquely identify a graphic object . The following functions are used to get the graphic handle .
Function | Purpose |
|---|---|
gca() | Get the handle of the current coordinate axis |
gcf() | Get the handle of the current image |
allchild(handle_list) | Get the handle of all child objects of this object |
ancestor(h,type) | Get the latest type Ancestor nodes of type |
delete(h) | Delete an object |
findall(handle_list) | Get the descendants of this object |
All drawing functions also return handles to graphic objects .
Manipulate graphic attributes through graphic handles
Use get() and set() Function can access and modify the attributes of graphic objects . visit Official documents You can view the properties of all graphic objects .
set(H,Name,Value)v = get(h,propertyName)
The following two examples demonstrate the use of graphic handles to manipulate graphic objects :
Change axis properties :
% The first picture
set(gca, 'FontSize', 25);
% The second picture
set(gca, 'XTick', 0:pi/2:2*pi);
set(gca, 'XTickLabel', 0:90:360);
% The third picture
set(gca, 'FontName', 'symbol');
set(gca, 'XTickLabel', {'0', 'p/2', 'p', '3p/2', '2p'});Change Linetype
h = plot(x,y); set(h, 'LineStyle','-.', ... 'LineWidth', 7.0, ... 'Color', 'g');
Save the drawing to a file
Use saveas(fig,filename) The command saves drawing objects to a file , among fig For graphics handle ,filname For the file name .
saveas(gcf, 'myfigure.png')
Draw advanced charts
Two dimensional charts
Broken line diagram
function | Graphic description |
|---|---|
loglog() | x Axis and y The axes take logarithmic coordinates |
semilogx() | x The axis takes logarithmic coordinates ,y The axis takes linear coordinates |
semilogy() | x The axis takes linear coordinates ,y The axis takes logarithmic coordinates |
plotyy() | With two sets y Linear coordinate system of coordinate axis |
ploar() | Polar system |
Logarithmic coordinate system drawing line
The following example demonstrates the logarithmic coordinate system line :
x = logspace(-1,1,100); y = x.^2;
subplot(2,2,1);
plot(x,y);
title('Plot');
subplot(2,2,2);
semilogx(x,y);
title('Semilogx');
subplot(2,2,3);
semilogy(x,y);
title('Semilogy');
subplot(2,2,4);
loglog(x, y);
title('Loglog'); Logarithmic coordinate system can be added grid , To distinguish between linear coordinate system and logarithmic coordinate system .
set(gca, 'XGrid','on');
double y Axis line
plotyy() The return value of is array [ax,hlines1,hlines2], among :
axIt's a vector , Save the handle of two coordinate system objects .hlines1andhlines2They are the handles of two graph lines .
x = 0:0.01:20;
y1 = 200*exp(-0.05*x).*sin(x);
y2 = 0.8*exp(-0.5*x).*sin(10*x);
[AX,H1,H2] = plotyy(x,y1,x,y2);
set(get(AX(1),'Ylabel'),'String','Left Y-axis')
set(get(AX(2),'Ylabel'),'String','Right Y-axis')
title('Labeling plotyy');
set(H1,'LineStyle','--'); set(H2,'LineStyle',':');Statistical charts
function | Graphic description |
|---|---|
hist() | Histogram |
bar() | Two dimensional histogram |
pie() | The pie chart |
stairs() | Stairs |
stem() | Needle pattern |
Histogram
Histogram
Use bar() and bar3() Function to draw two-dimensional and three-dimensional histograms respectively
x = [1 2 5 4 8]; y = [x;1:5];
subplot(1,3,1); bar(x); title('A bargraph of vector x');
subplot(1,3,2); bar(y); title('A bargraph of vector y');
subplot(1,3,3); bar3(y); title('A 3D bargraph');
histIt is mainly used to view the frequency distribution of variables , andbarIt is mainly used to view the statistical results of discrete quantities .
Use barh() Function can draw a histogram of vertical arrangement
x = [1 2 5 4 8];
y = [x;1:5];
barh(y);
title('Horizontal'); towards bar() Pass in 'stack' Parameter allows the histogram to be drawn in the form of a stack .
x = [1 2 5 4 8];
y = [x;1:5];
bar(y,'stacked');
title('Stacked');The pie chart
Use pie() and pie3() You can draw two-dimensional and three-dimensional pie charts . Pass a bool The vector indicates whether each sector is offset .
a = [10 5 20 30]; subplot(1,3,1); pie(a); subplot(1,3,2); pie(a, [0,0,0,1]); subplot(1,3,3); pie3(a, [0,0,0,1]);
Ladder diagram and needle diagram : Draw a sequence of discrete numbers
stairs() and stem() Function is used to draw ladder graph and needle graph respectively , Used to represent a sequence of discrete numbers .
x = linspace(0, 4*pi, 40); y = sin(x); subplot(1,2,1); stairs(y); subplot(1,2,2); stem(y);
Three dimensional chart
Convert a two-dimensional map to a three-dimensional map
stay MATLAB in , All drawings are three-dimensional , A two-dimensional picture is just a projection of a three-dimensional picture . Click... In the graphics window Rotate 3D Button , You can drag and drop the mouse to view the 3D view of the drawing .
Convert a three-dimensional drawing to a two-dimensional drawing
Use imagesc() Function can convert a three-dimensional view into a two-dimensional top view , The height is indicated by the color of the dot .
[x, y] = meshgrid(-3:.2:3,-3:.2:3); z = x.^2 + x.*y + y.^2; subplot(1, 2, 1) surf(x, y, z); subplot(1, 2, 2) imagesc(z);
Use colorbar The command can add the legend of the corresponding relationship between color and height on the generated two-dimensional map , Use colormap Command can change the color scheme . For details, please refer to Official documents
Three dimensional drawing
Preparation before drawing a three-dimensional map
- Use
meshgrid()Generate 2D mesh
meshgrid() Function expands the two input vectors by corresponding row expansion and column expansion to obtain two augmented matrices , The binary function can be applied to this matrix .
x = -2:1:2; y = -2:1:2; [X,Y] = meshgrid(x,y) Z = X.^2 + Y.^2
Draw 3D lines
Use plot3() Function to draw a three-dimensional surface , Input should be three vectors .
x=0:0.1:3*pi; z1=sin(x); z2=sin(2.*x); z3=sin(3.*x);
y1=zeros(size(x)); y3=ones(size(x)); y2=y3./2;
plot3(x,y1,z1,'r',x,y2,z2,'b',x,y3,z3,'g'); grid on;
xlabel('x-axis'); ylabel('y-axis'); zlabel('z-axis');Draw a 3D face
Use mesh() and surf() The command can draw 3D faces , The former does not fill the mesh while the latter .
x = -3.5:0.2:3.5; y = -3.5:0.2:3.5; [X,Y] = meshgrid(x,y); Z = X.*exp(-X.^2-Y.^2); subplot(1,2,1); mesh(X,Y,Z); subplot(1,2,2); surf(X,Y,Z);
Draw contour lines of 3D graphics
Use contour() and contourf() Function can draw contour lines of 3D graphics , The former does not fill the mesh while the latter .
towards contour() The function can change the details of the image by passing in parameters or manipulating the graphic handle :
x = -3.5:0.2:3.5; y = -3.5:0.2:3.5; [X,Y] = meshgrid(x,y); Z = X.*exp(-X.^2-Y.^2); subplot(1,3,1); contour(Z,[-.45:.05:.45]); axis square; subplot(1,3,2); [C,h] = contour(Z); clabel(C,h); axis square; subplot(1,3,3); contourf(Z); axis square;
Use meshc() and surfc() Function can draw its contour lines when drawing a three-dimensional figure .
x = -3.5:0.2:3.5; y = -3.5:0.2:3.5; [X,Y] = meshgrid(x,y); Z = X.*exp(-X.^2-Y.^2); subplot(1,2,1); meshc(X,Y,Z); subplot(1,2,2); surfc(X,Y,Z);
Draw a three-dimensional volume
Use patch() Function can draw a three-dimensional body .
v = [0 0 0; 1 0 0 ; 1 1 0; 0 1 0; 0.25 0.25 1; 0.75 0.25 1; 0.75 0.75 1; 0.25 0.75 1];
f = [1 2 3 4; 5 6 7 8; 1 2 6 5; 2 3 7 6; 3 4 8 7; 4 1 5 8];
subplot(1,2,1);
patch('Vertices', v, 'Faces', f, 'FaceVertexCData', hsv(6), 'FaceColor', 'flat');
view(3); axis square tight; grid on;
subplot(1,2,2);
patch('Vertices', v, 'Faces', f, 'FaceVertexCData', hsv(8), 'FaceColor','interp');
view(3); axis square tight; grid onPerspective and lighting of three-dimensional drawings
Adjust the perspective
Use view() Function can adjust the perspective ,view() Function accepts two floating-point arguments , Represent two azimuth angles respectively azimuth and elevation.
sphere(50); shading flat; material shiny; axis vis3d off; view(-45,20);
Symbolic operations
Create symbolic variables
Create symbolic numbers
Use sym Function can create symbolic numbers . Using symbolic numbers can accurately save irrational numbers , There will be no error .
sym(1/3) % obtain 1/3 1/3 % obtain 0.3333
Saving irrational numbers as symbolic numbers can avoid the error of converting them into floating-point numbers :
sin(sym(pi)) % obtain 0 sin(pi) % obtain 1.2246e-16
Create symbolic variables
Use sym and syms You can create symbolic variables , The difference lies in :
sym Only one symbolic variable can be created at a time , and syms You can create multiple symbolic variables at a time .
syms a % sym Command can only create one symbolic variable syms b c d % syms Command can create multiple symbolic variables
If the specified symbolic variable already exists ,sym It will not retain its original value , and syms Will clear its value .
syms x y f = x+y; % Implicitly create symbolic variables f sym f % Do not empty variables f Original value , namely f = x + y
syms x y f = x+y; % Implicitly create symbolic variables f syms f % Empty variables f Original value , namely f = f
Use sym You can create a symbolic variable matrix .
A = sym('a', [2 5]) % Create a 2*5 Symbolic variable matrix of
whosThe output is as follows :
A = [ a1_1, a1_2, a1_3, a1_4, a1_5] [ a2_1, a2_2, a2_3, a2_4, a2_5] Name Size Bytes Class Attributes A 2x5 112 sym
A combination of sym and syms You can quickly create a series of variables with subscripts
clear all
syms(sym('a', [1 5]))
whosThe output is as follows :
Name Size Bytes Class Attributes a1 1x1 8 sym a2 1x1 8 sym a3 1x1 8 sym a4 1x1 8 sym a5 1x1 8 sym
Symbolic operations
Simplification and substitution of symbolic expressions
Simplification of symbolic expressions
Use simplify() Functions can simplify symbolic expressions .
syms x a b c simplify(sin(x)^2 + cos(x)^2); % obtain 1 simplify(exp(c*log(sqrt(a+b)))); % obtain (a + b)^(c/2)
The standard of expression simplification is uncertain , The following three functions simplify the expression according to different standards :
expand() Functions can expand expressions
syms x f = (x ^2- 1)*(x^4 + x^3 + x^2 + x + 1)*(x^4 - x^3 + x^2 - x + 1); expand(f); % obtain x^10 - 1
factor() Functions can be factorized
syms x g = x^3 + 6*x^2 + 11*x + 6; factor(g); % obtain (x + 3)*(x + 2)*(x + 1)
horner() Functions can change polynomials into nested forms
syms x h = x^5 + x^4 + x^3 + x^2 + x; horner(h); % obtain x*(x*(x*(x*(x + 1) + 1) + 1) + 1)
Substitution of symbolic expressions
Use sub(expr, old, new) The function can express a symbolic expression expr Medium old Replace with new.
syms x y f = x^2*y + 5*x*sqrt(y); subs(f, x, 3); % obtain 9*y + 15*y^(1/2)
Find the analytical solution of the equation
Use solve(eqn,var) and solve(eqns,vars) The analytical solution of the equation can be obtained .
Solve the univariate equation
Use == Define an equation , And call solve Function solving .( If not specified == The value to the right of the symbol , Then the default right side of the equation is 0.)
syms x eqn = x^3 - 6*x^2 == 6 - 11*x; solve(eqn); % obtain [1 2 3]
Solve multivariable equations
For multivariable equations , We need to specify which variable to solve .
syms x y eqn = [6*x^2 - 6*x^2*y + x*y^2 - x*y + y^3 - y^2 == 0]; solve(eqn, y); % obtain [1, 2*x, -3*x]
Solve equations
towards solve() The function can be introduced into the equation system to solve the equation .
syms u v eqns = [2*u + v == 0, u - v == 1]; S = solve(eqns,[u v]);
The solution of the equation can be indexed by the variable name , And the solution can be substituted into other expressions .
S.u; % obtain 1/3 S.v; % obtain -2/3 subs(3*v + u, S); % obtain -3/5
Symbolic calculus
Find the limit
Use limit(expr, var, a) Function can evaluate the symbolic expression expr In variables var Tend to be a The limit of time , Add parameter 'left' or 'right' You can specify the left limit or the right limit .
syms x; expr = 1/x; limit(expr,x,0); % obtain NaN limit(expr,x,0,'left'); % obtain -Inf limit(expr,x,0,'right'); % obtain Inf
differential
Use diff(expr, var, n) Function can evaluate the symbolic expression expr The variable var Of n First order differential .
syms a b c x; expr = a*x^2 + b*x + c; diff(expr, a); % obtain x^2 diff(expr, b); % obtain x diff(expr, x); % obtain b + 2*a*x diff(expr, x, 2); % obtain 2*a
integral
Use int(expr, var) Function can evaluate the symbolic expression expr The variable var The indefinite integral of . Use int(expr, var, [a, b]) Function can specify upper and lower bounds to calculate definite integral ,a and b It can be a symbolic expression .
syms x a b expr = -2*x/(1+x^2)^2; int(expr, x); % obtain 1/(x^2 + 1) int(expr, x, [1, 2]); % obtain -0.3 int(expr, x, [1, Inf]); % obtain -0.5 int(expr, x, [a, b]); % obtain 1/(b^2 + 1) - 1/(a^2 + 1)
For some functions ,MATLAB Its integral cannot be obtained , At this time MATLAB Will return an unresolved (unsolved) Integral form of .
syms x int(sin(sinh(x))); % An integral without solution ,MATLAB return int(sin(sinh(x)),
Sum of series
Use symsum(expr, k, [a b]) Calculation series expr The index of k from a To b The sum of .
syms k x symsum(k^2, k) % obtain k^3/3 - k^2/2 + k/6 symsum(k^2, k, [0 10]) % obtain 385 symsum(x^k/factorial(k),k,1,Inf) % obtain exp(x) - 1
Taylor expansion
Use taylor(expr,var,a) Calculation expression expr stay var=a The Taylor series at .
syms x taylor(exp(x)) % obtain x^5/120 + x^4/24 + x^3/6 + x^2/2 + x + 1 taylor(sin(x)) % obtain x^5/120 - x^3/6 + x taylor(cos(x)) % obtain x^4/24 - x^2/2 + 1
The plot
You can draw images of symbolic expressions , Common drawing functions are as follows :
function | effect |
|---|---|
fplot() | Draw a two-dimensional line image of a symbolic expression |
fplot3() | Draw a 3D line image of a symbolic expression |
ezpolar() | Draw the polar marking image of the symbolic expression |
fmesh() | Draw a mesh image |
fsurf() | Draw a colored face image |
fcontour() | Draw a contour image |
fimplicit() | Draw an image of implicit functional relationships |
The following example shows the drawing of two-dimensional and three-dimensional line images
subplot(1, 2, 1) syms x f = x^3 - 6*x^2 + 11*x - 6; fplot(f, x) subplot(1, 2, 2) syms t fplot3(t^2*sin(10*t), t^2*cos(10*t), t)
The following example demonstrates the rendering of three-dimensional surfaces
syms x y fsurf(x^2 + y^2)
The following example demonstrates the drawing of implicit function relation image
syms x y eqn = (x^2 + y^2)^4 == (x^2 - y^2)^2; fimplicit(eqn, [-1 1])
Numerical calculation
Numerical operation of polynomials
Use MATLAB Represents a polynomial
Use vectors to represent polynomials
stay MATLAB in , Polynomials can be represented by vectors , The elements in the vector are the coefficients of polynomials ( Descending order ): The first is the coefficient of the highest order of the polynomial , The last digit is the constant term .
For example, polynomials : f(x) = x^3 - 2x - 5f(x)=x3−2x−5
You can use vectors p = [1 0 -2 -5] Express .
Polynomial evaluation :polyval()
Use polyval(p, x) You can calculate polynomials p stay x The value at each point .
a = [9,-5,3,7]; x = -2:0.01:5; f = polyval(a,x); plot(x,f);
Multiplication of polynomials :conv()
Use conv(p1, p2) Function can be applied to two vectors p1 and p2 Convolution multiplication , Used to calculate the multiplication of polynomials .
For example, polynomials : f(x) = (x^2+1) (2x+7)f(x)=(x2+1)(2x+7)
have access to conv() Function to get the expanded polynomial :
p = conv([1 0 1], [2 7])
obtain p = [2 7 2 7].
Numerical operation of polynomials
Factorization of polynomials :roots()
Use roots(p) Functions can be polynomial p Do factorization , That is, the expression value is 0 The root of the .
p = roots([1 -3.5 2.75 2.125 -3.875 1.25])
obtain p = [2 -1, 1+0.5i, 1-0.5i, 0.5], Express x^5 -3.5 x^4 +2.75 x^3 + 2.125 x^2 + -3.875 x+1.25 = (x-2)(x+1)(x-1-0.5i)(x-1+0.5i)(x-0.5)x5−3.5x4+2.75x3+2.125x2+−3.875x+1.25=(x−2)(x+1)(x−1−0.5i)(x−1+0.5i)(x−0.5).
Differentiation of polynomials :polyder()
Use polyder(p) Functions can calculate the derivatives of polynomials .
For example, take the derivative of the following polynomial : f(x) = 5x^4 - 2x^2 + 1f(x)=5x4−2x2+1
p = polyder([5 0 -2 0 1]);
obtain p = [20 0 -4 0], Means the derivative obtained by calculation f’(x) = 20 x^3 - 4xf′(x)=20x3−4x.
The integral of a polynomial :polyint()
Use polyint(p, k) Functions can calculate polynomials p Integral , The constant term of the integration result is set as k.
For example, take the derivative of the following polynomial : f(x) = 5x^4 - 2x^2 + 1f(x)=5x4−2x2+1
p = polyint([5 0 -2 0 1], 3)
obtain p = [1 0 -0.6667 0 1 3], It means the integral obtained by calculation \int f(x) dx = x^5 -0.6667x^3 + x + 3∫f(x)dx=x5−0.6667x3+x+3.
Numerical operation of nonlinear expressions
equation ( Group ) Root seeking fsolve()
Use fsolve(fun, x0) Find the root of nonlinear equations ,fun Is the function handle of the equation to be solved ,x0 For the initial value .
Find the equation 1.2x+x\sin(x)+0.3=01.2x+xsin(x)+0.3=0 stay x=0x=0 Near solution .
f2 = @(x) (1.2*x+x*sin(x)+0.3); fsolve(f2,0) % obtain -0.3500
Solve equations \begin{aligned} \left\{ \begin{aligned} e^{-e^{-(x_1+x_2)}} - x_2(1+x_1^2) = 0 \\ x_1 \cos x_2 + x_2 \sin x_1 - \frac{1}{2} = 0 \end{aligned} \right. \end{aligned}⎩⎪⎨⎪⎧e−e−(x1+x2)−x2(1+x12)=0x1cosx2+x2sinx1−21=0
Set the initial value as [0, 0][0,0]
fun = @(x) [exp(-exp(-(x(1)+x(2))))-x(2)*(1+x(1)^2)...
x(1)*cos(x(2)) + x(2)*sin(x(1)) - 0.5]
x0 = [0,0];
x = fsolve(fun,x0) % obtain [0.3532 0.6061]Numerical differentiation
Find the difference :diff()
Use diff(X, n) Calculate the vector X Of n Order difference ,n The default is 1.
x = [1 2 5 2 1]; diff(x); % obtain [1 3 -3 -1] diff(x,1); % obtain [1 3 -3 -1] diff(x,2); % obtain [2 -6 2]
Find the derivative :diff(y)./diff(x)
Use the definition of derivative
You can calculate the approximate derivative of a function at a certain point .
The following program calculates f(x) = x^3f(x)=x3 The value of the first and second derivatives of .
x = -2:0.005:2; y = x.^3;
m = diff(y)./diff(x); % Calculate the first derivative
m2 = diff(m)./diff(x(1:end-1)); % Calculate the second derivative
plot(x,y,x(1:end-1),m,x(1:end-2),m2);
xlabel('x'); ylabel('y');
legend('f(x) =x^3','f''(x)','f''''(x)', 4);Numerical integration
The principle of numerical integration
There are three common algorithms for calculating numerical integrals : Rectangular method , Trapezoidal method , Parabola method , They treat the graphs of differential intervals as rectangles , trapezoid , Parabola to calculate the area .
The following three methods are used to calculate f(x) = 4x^3f(x)=4x3 In the interval (0, 2)(0,2) Integral in .
h = 0.05; x = 0:h:2; % Use the rectangular method to calculate the approximate integral midpoint = (x(1:end-1)+x(2:end))./2; y = 4*midpoint.^3; s = sum(h*y) % obtain 15.9950 % Use the trapezoidal method to calculate the approximate integral trapezoid = (y(1:end-1)+y(2:end))/2; s = h*sum(trapezoid) % obtain 15.2246 % Use parabola method to calculate numerical integration s = h/3*(y(1)+2*sum(y(3:2:end-2))+4*sum(y(2:2:end))+y(end)) % obtain 15.8240
Numerical integral function :integral()
integral(),integral2(),integral3() For functions in xmin to xmax Carry out a heavy , double , Triple integral .
Their first argument should be a function handle , The following example demonstrates their usage :
Calculation \int_0^2 \frac{1}{x^3-2x-5}∫02x3−2x−51
f = @(x) 1./(x.^3-2*x-5); integral(f,0,2) % obtain -0.4605
Calculation \int_0^\pi \int_\pi^{2\pi} (y\sin(x) + x \cos(y)) dx dy∫0π∫π2π(ysin(x)+xcos(y))dxdy
f = @(x,y) y.*sin(x)+x.*cos(y); integral2(f,pi,2*pi,0,pi) % obtain -9.8696
Calculation \int_{-1}^1 \int_0^1 \int_0^\pi (y\sin(x) + z \cos(y)) dx dy dz∫−11∫01∫0π(ysin(x)+zcos(y))dxdydz
f = @(x,y,z) y.*sin(x)+z.*cos(y); integral3(f,0,pi,0,1,-1,1)
Statistics and fitting
Statistics
Descriptive statistics (Descriptive Statistics)
Descriptive statistics mainly studies data The central trend (Central Tendency) and Variation
The central trend (Central Tendency)
function | effect |
|---|---|
mean() | Calculate average |
median() | Calculate the median |
mode() | Calculate the mode |
prctile(X,num) | data X Of num% What is the quantile |
max() | Calculate the maximum |
min() | Calculate the minimum |
The following functions plot statistical charts :
function | effect |
|---|---|
bar() | Draw a bar graph |
stem() | Draw a needle chart |
area() | Draw a fill chart |
boxplot() | Draw box lines |
x = 1:14; freqy = [1 0 1 0 4 0 1 0 3 1 0 0 1 1]; subplot(1,3,1); bar(x,freqy); xlim([0 15]); subplot(1,3,2); area(x,freqy); xlim([0 15]); subplot(1,3,3); stem(x,freqy); xlim([0 15]);
Boxplot can highlight the quartile of data .
marks = [80 81 81 84 88 92 92 94 96 97]; boxplot(marks) % prctile(marks, [25 50 75]) % obtain [81 90 94]
Variation
The degree of dispersion
function | effect |
|---|---|
std() | Calculate the standard deviation of the data |
var() | Calculate the variance of the data |
skewness (Skewness
function | effect |
|---|---|
skewness() | Calculate the skewness of the data |
Skewness reflects the degree of symmetry of data
- When the data deviates to the left , Its skewness is less than 0.
- When the data is completely symmetrical , Its skewness is equal to 0.
- When the data is biased to the right , Its skewness is greater than 0.
X = randn([10 3]); % structure 10*3 Matrix
X(X(:,1)<0, 1) = 0; % Shift the first column of data to the right
X(X(:,3)>0, 3) = 0; % Shift the second column of data to the left
boxplot(X, {'Right-skewed', 'Symmetric', 'Left-skewed'});
skewness(X); % obtain [0.5162 -0.7539 -1.1234]kurtosis (Kurtosis)
function | effect |
|---|---|
kurtosis() | Calculate the kurtosis of the data |
kurtosis (Kurtosis) It represents the peak value of probability density distribution curve at the mean value . Intuitive to see , The kurtosis reflects the sharpness of the peak .
Statistical inference (Inferential Statistics)
The core of inferential statistics is hypothesis testing . The following functions are used for hypothesis testing .
function | effect |
|---|---|
ttest() | Conduct T test |
ztest() | Conduct Z test |
ranksum() | Perform rank sum test |
signrank() | Sign rank test |
load examgrades x = grades(:,1); y = grades(:,2); [h,p] = ttest(x,y);
Carry out the above procedure , obtain [h p] = [0 0.9805], Indicates at the default significance level (5%) Next, we have no reason to refuse x And y Homodistribution .
fitting
Polynomial fitting
Univariate polynomial fitting :polyfit()
Use polyfit(x, y, n) Function on data x and y Conduct n Quadratic polynomial fitting .
x = [-1.2 -0.5 0.3 0.9 1.8 2.6 3.0 3.5];
y = [-15.6 -8.5 2.2 4.5 6.6 8.2 8.9 10.0];
for i = 1:3 % Once each , secondary , Cubic fitting
p = polyfit(x, y, i);
xfit = x(1):0.1:x(end); yfit = polyval(p, xfit);
subplot(1, 3, i); plot(x, y, 'ro', xfit, yfit);
legend('Data points', 'Fitted curve', 'Location', 'southeast');
end Multivariate linear fitting :regress()
Use regress(y, X) Function on data X and y Do multiple linear regression .
load carsmall;
y = MPG; x1 = Weight; x2 = Horsepower; % Import dataset
X = [ones(length(x1),1) x1 x2]; % Build augmentation X matrix
b = regress(y,X); % Do a linear regression
% The following is the drawing statement
x1fit = min(x1):100:max(x1); x2fit = min(x2):10:max(x2);
[X1FIT,X2FIT] = meshgrid(x1fit,x2fit);
YFIT = b(1)+b(2)*X1FIT+b(3)*X2FIT;
scatter3(x1,x2,y,'filled'); hold on;
mesh(X1FIT,X2FIT,YFIT); hold off;
xlabel('Weight'); ylabel('Horsepower'); zlabel('MPG'); view(50,10);Nonlinear fitting
For nonlinear fitting , You need to use the curve fitting toolbox . Enter... In the command window cftool() Open the curve fitting toolbox .
interpolation
One dimensional interpolation
function | effect |
|---|---|
interp1(x,v) or interp1(x,v,xq) | linear interpolation |
spline(x,v) or spline(x,v,xq) | Cubic spline interpolation |
pchip(x,v) or pchip(x,v,xq) | Three times Hermite interpolation |
mkpp(breaks,coefs) | Generate piecewise polynomials |
ppval(pp,xq) | Calculate the interpolation result of piecewise polynomial |
The following example demonstrates the use of interp1(x, v, xq) Perform linear interpolation and use spline(x, v, xq) Perform cubic spline interpolation . The meanings of the parameters are as follows :
x,v: Sample points to be interpolated .xq: Query point , Function returns the interpolation result at these points .
% Structural data
x = linspace(0, 2*pi, 40); x_m = x; x_m([11:13, 28:30]) = NaN;
y_m = sin(x_m);
plot(x_m, y_m, 'ro', 'MarkerFaceColor', 'r'); hold on;
% Linear interpolation of data
m_i = ~isnan(x_m);
y_i = interp1(x_m(m_i), y_m(m_i), x);
plot(x,y_i, '-b'); hold on;
% Perform cubic spline interpolation on the data
m_i = ~isnan(x_m);
y_i = spline(x_m(m_i), y_m(m_i), x);
plot(x,y_i, '-g');
legend('Original', 'Linear', 'Spline');Two dimensional interpolation
Use interp2() Can carry out two-dimensional interpolation , To whom method Parameter input string can specify interpolation algorithm .
Method | explain | Continuity |
|---|---|---|
'linear' | ( Default ) The value inserted at the query point is based on the linear interpolation of the value at the grid point of the adjacent point in each dimension . | C0 |
'spline' | The value inserted at the query point is based on the cubic interpolation of the value at the grid point of the adjacent point in each dimension . Interpolation is based on cubic splines using non knot termination conditions . | C2 |
'nearest' | The value inserted at the query point is the value closest to the sample grid point . | Discontinuous |
'cubic' | The value inserted at the query point is based on the cubic interpolation of the value at the grid point of the adjacent point in each dimension . Interpolation is based on cubic convolution . | C1 |
'makima' | The modified Akima Three times Hermite interpolation . The value inserted at the query point is based on the maximum number of times 3 Piecewise functions of polynomials , Use the values of adjacent grid points in each dimension for calculation . To prevent overshoot , Improved Akima The formula . | C1 |
% Build sample points xx = -2:.5:2; yy = -2:.5:3; [x,y] = meshgrid(xx,yy); xx_i = -2:.1:2; yy_i = -2:.1:3; [x_i,y_i] = meshgrid(xx_i,yy_i); z = x.*exp(-x.^2-y.^2); % linear interpolation subplot(1, 2, 1); z_i = interp2(xx,yy,z,x_i,y_i); surf(x_i,y_i,z_i); hold on; plot3(x,y,z+0.01,'ok','MarkerFaceColor','r'); hold on; % Cubic interpolation subplot(1, 2, 2); z_ic = interp2(xx,yy,z,x_i,y_i, 'spline'); surf(x_i,y_i,z_ic); hold on; plot3(x,y,z+0.01,'ok','MarkerFaceColor','r'); hold on;
边栏推荐
- 2022 PMP project management examination agile knowledge points (9)
- Leecode brush question record sword finger offer 58 - ii Rotate string left
- 在docker中快速使用各个版本的PostgreSQL数据库
- kubernetes部署ldap
- Wechat applet UploadFile server, wechat applet wx Uploadfile[easy to understand]
- web渗透测试是什么_渗透实战
- 从外企离开,我才知道什么叫尊重跟合规…
- GPIO简介
- Uniapp uploads and displays avatars locally, and converts avatars into Base64 format and stores them in MySQL database
- 沉浸式投影在线下展示中的三大应用特点
猜你喜欢
MySQL learning notes (mind map)
Jenkins' user credentials plug-in installation
三维扫描体数据的VTK体绘制程序设计

1000 words selected - interface test basis
![[2022 the finest in the whole network] how to test the interface test generally? Process and steps of interface test](/img/8d/b59cf466031f36eb50d4d06aa5fbe4.jpg)
[2022 the finest in the whole network] how to test the interface test generally? Process and steps of interface test

48 page digital government smart government all in one solution
工程师如何对待开源 --- 一个老工程师的肺腑之言
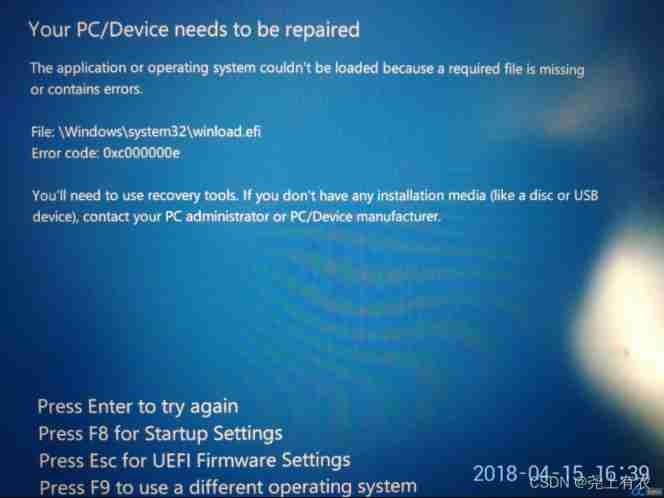
Win10 startup error, press F9 to enter how to repair?
DAY ONE
File and image comparison tool kaleidoscope latest download
随机推荐
准备好在CI/CD中自动化持续部署了吗?
MIT 6.824 - raft Student Guide
Oracle EMCC 13.5 environment in docker every minute
互动滑轨屏演示能为企业展厅带来什么
Personal digestion of DDD
GPIO簡介
DAY FOUR
Understand the misunderstanding of programmers: Chinese programmers in the eyes of Western programmers
Building lease management system based on SSM framework
Pdf document signature Guide
Leecode brush question record sword finger offer 58 - ii Rotate string left
JWT signature does not match locally computed signature. JWT validity cannot be asserted and should
MIT 6.824 - Raft学生指南
沉浸式投影在线下展示中的三大应用特点
PXE server configuration
三维扫描体数据的VTK体绘制程序设计
Common shortcuts to idea
1000字精选 —— 接口测试基础
How engineers treat open source -- the heartfelt words of an old engineer
刘永鑫报告|微生物组数据分析与科学传播(晚7点半)