当前位置:网站首页>Matlab学习10-图像处理之傅里叶变换
Matlab学习10-图像处理之傅里叶变换
2022-08-03 11:30:00 【CHengYuP】
前言
图像变换
- 一维离散变换
- 二维离散变换
- 傅里叶变换
- 离散余弦变换
Matlab学习10-图像处理之傅里叶变换
傅里叶变换
优点:能从空间域和频率域两个不同的角度来看待问信号或图像。
缺点:傅里叶变换的收敛速度慢。
一、离散傅里叶变换
效果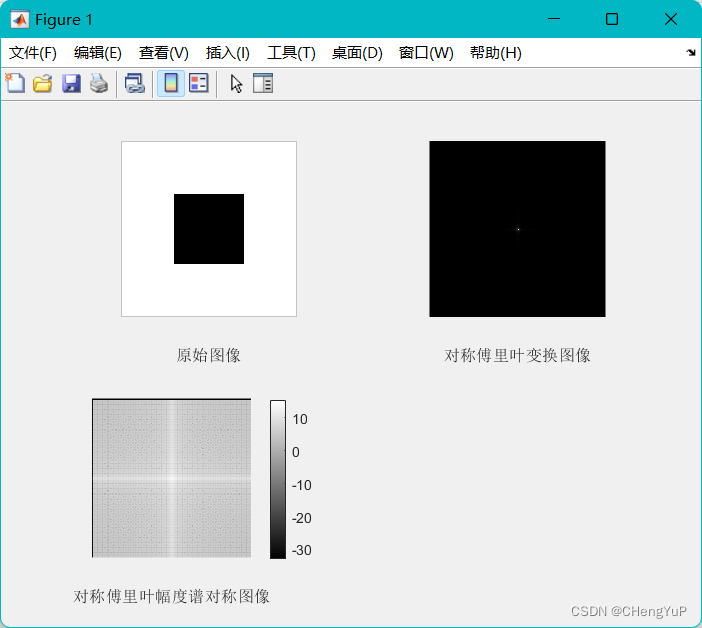
代码
% 离散傅里叶变换示例。显示二维图、对称傅里叶幅度谱图像和傅里叶幅度图对数图像。
fxy=imread("img/F5_11a.bmp");
fxy=rgb2gray(fxy);
subplot(2,2,1),imshow(fxy),xlabel('原始图像');
Fuv=fft2(fxy);
FftShiftAbs=fftshift(abs(Fuv));
subplot(2,2,2),imshow(FftShiftAbs,[]),xlabel('对称傅里叶变换图像');
LogFftShiftAbs=log(FftShiftAbs);
subplot(2,2,3),imshow(LogFftShiftAbs,[]),xlabel('对称傅里叶幅度谱对称图像'),colormap(gray),colorbar;
二、二维离散傅里叶变换
效果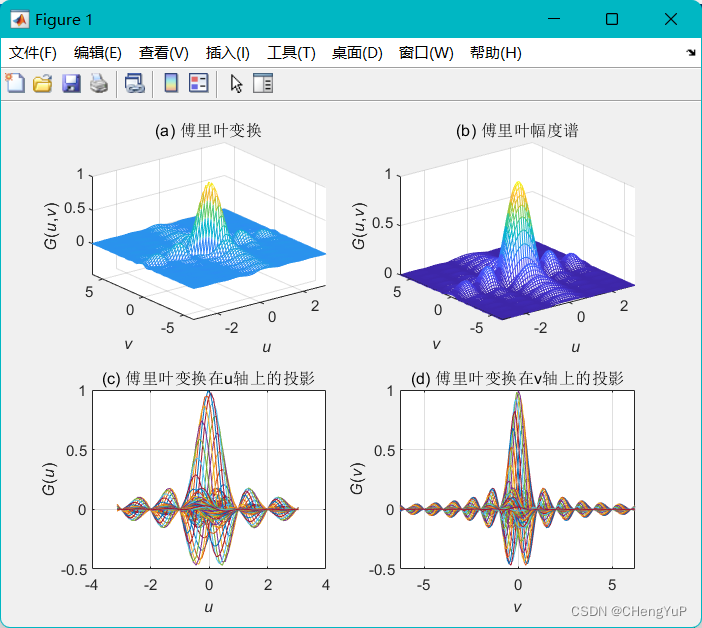
代码
% 二维离散傅里叶变换原理示例,显示二维图、傅里叶变换后的图,对称傅里叶幅度谱图像和他们的三维示意图。
A=1;
X=1;
Y=1;
uu=-1*pi:0.1:1*pi;
vv=-2*pi:0.1:2*pi;
[u,v]=meshgrid(uu,vv);
Fuv=A*X*Y*(sin(pi*u*X).*exp(-j*pi*u*X)./(pi*u*X)).*(sin(pi*v*Y).*exp(-j*pi*v*Y)./(pi*v*Y));
subplot(2,2,1),mesh(u,v,real(Fuv)),xlabel('\itu'),ylabel('\itv'),zlabel('{\itG}({\itu},{\itv})'),title('(a) 傅里叶变换');
subplot(2,2,2),mesh(u,v,abs(Fuv)),xlabel('\itu'),ylabel('\itv'),zlabel('{\itG}({\itu},{\itv})'),title('(b) 傅里叶幅度谱');
subplot(2,2,3),plot(uu,Fuv),xlabel('\itu'),ylabel('{\itG}({\itu})'),title('(c) 傅里叶变换在u轴上的投影'),grid on;
subplot(2,2,4),plot(vv,Fuv),xlabel('\itv'),ylabel('{\itG}({\itv})'),title('(d) 傅里叶变换在v轴上的投影'),grid on;
三、傅里叶级数将周期函数转换为不同正弦波的叠加
效果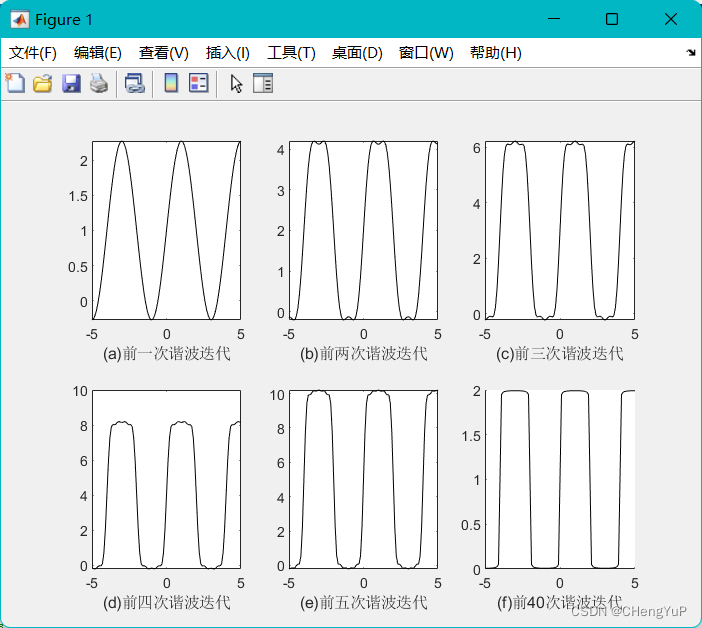
代码
% 使用傅里叶级数将周期函数转换为不同正弦波的叠加。
A=2;
x=-5:0.1:5;
%前一次谐波叠代
hold on;
fx1=A/2+2*A/pi*(sin(1*pi*x/2)/1);
fxdd1=fx1;
subplot(2,3,1),plot(x,fxdd1,'k'),xlabel('(a)前一次谐波迭代');
%前两次谐波叠代
hold on;
fx2=A/2+2*A/pi*(sin(1*pi*x/2)/1+sin(3*pi*x/2)/3);
fxdd2=fx1+fx2;
subplot(2,3,2),plot(x,fxdd2,'k'),xlabel('(b)前两次谐波迭代');
%前三次谐波叠代
hold on;
fx3=A/2+2*A/pi*(sin(1*pi*x/2)/1+sin(3*pi*x/2)/3+sin(5*pi*x/2)/5);
fxdd3=fx1+fx2+fx3;
subplot(2,3,3),plot(x,fxdd3,'k'),xlabel('(c)前三次谐波迭代');
%前四次谐波叠代
hold on;
fx4=A/2+2*A/pi*(sin(1*pi*x/2)/1+sin(3*pi*x/2)/3+sin(5*pi*x/2)/5+sin(7*pi*x/2)/7);
fxdd4=fx1+fx2+fx3+fx4;
subplot(2,3,4),plot(x,fxdd4,'k'),xlabel('(d)前四次谐波迭代');
%前五次谐波叠代
hold on;
fx5=A/2+2*A/pi*(sin(1*pi*x/2)/1+sin(3*pi*x/2)/3+sin(5*pi*x/2)/5+sin(7*pi*x/2)/7+sin(9*pi*x/2)/9);
fxdd5=fx1+fx2+fx3+fx4+fx5;
subplot(2,3,5),plot(x,fxdd5,'k'),xlabel('(e)前五次谐波迭代');
%前四十次谐波叠代
hold on;
syms n;
k=symsum(2*A/pi*sin((2*n+1)*pi*x/2)/(2*n+1),0,39);
fxdd80=A/2+subs(k);
subplot(2,3,6),plot(x,fxdd80,'k'),xlabel('(f)前40次谐波迭代'),box off;
边栏推荐
- 成为优秀架构师必备技能:怎样才能画出让所有人赞不绝口的系统架构图?秘诀是什么?快来打开这篇文章看看吧!...
- hystrix 服务熔断和服务降级
- Analysis of the idea of the complete knapsack problem
- 优维低代码:Provider 构件
- Machine Learning (Chapter 1) - Feature Engineering
- What is the ERC20 token standard?
- Redis发布订阅和数据类型
- asdn涨薪技术之apifox+Jenkins如何玩转接口自动化测试
- 什么是bin文件?「建议收藏」
- build --repot
猜你喜欢

【倒计时5天】探索音画质量提升背后的秘密,千元大礼等你来拿
多态详细讲解(简单实现买票系统模拟,覆盖/重定义,多态原理,虚表)

GET 和 POST 有什么区别?
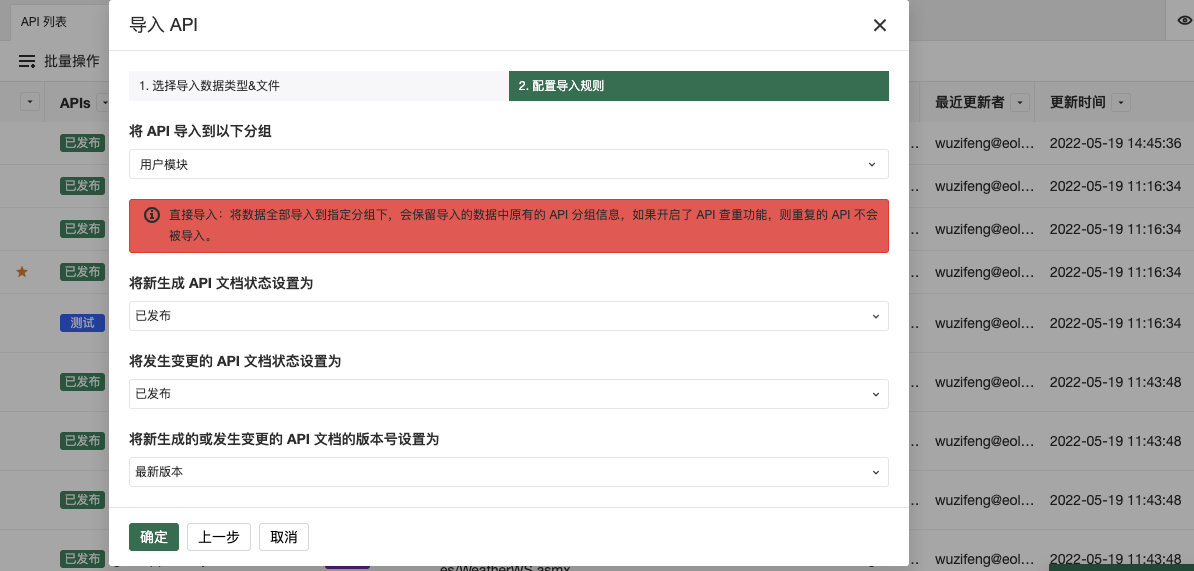
在线生成接口文档
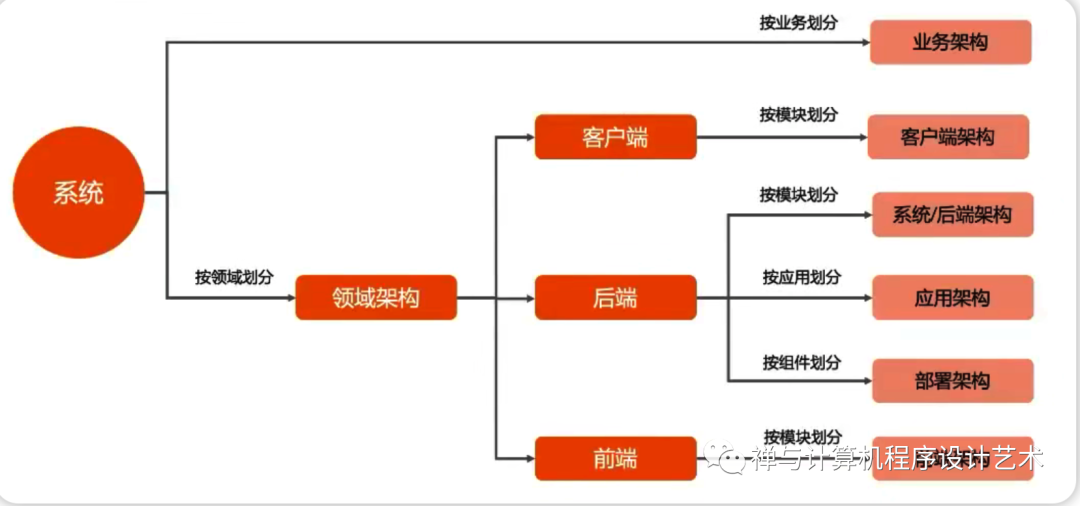
Skills required to be a good architect: How to draw a system architecture that everyone will love?What's the secret?Come and open this article to see it!...
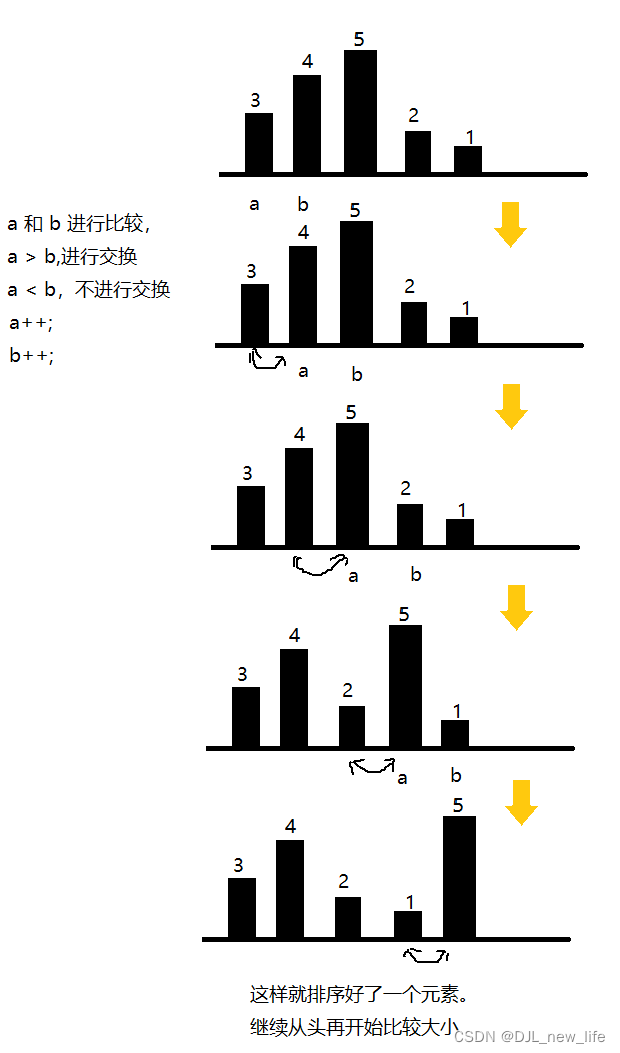
【冒泡排序以及奇数偶数排列】

基于PHP7.2+MySQL5.7的回收租凭系统
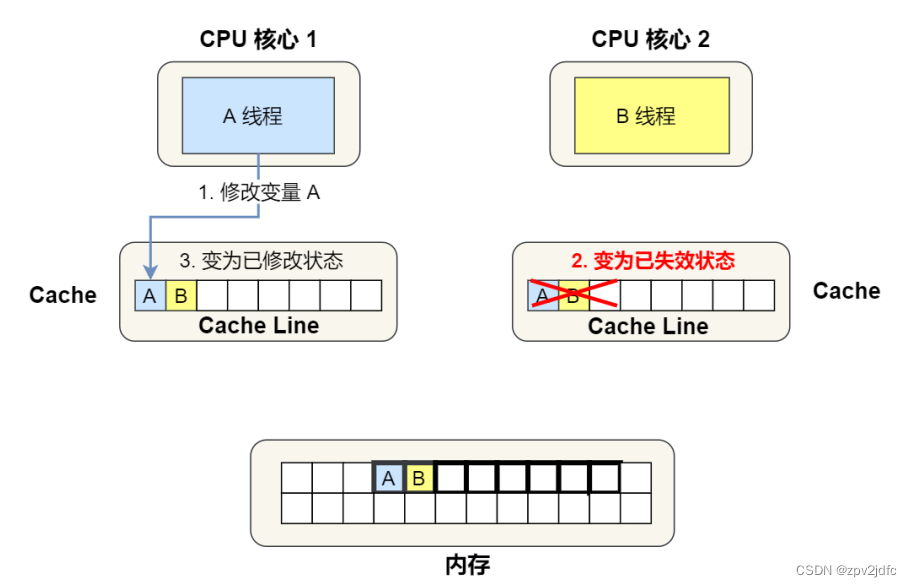
缓存--伪共享问题
![[LeetCode—Question 2 Sum of Two Numbers Detailed Code Explanation ] The source code is attached, which can be copied directly](/img/19/a3f58d5a1150d99571205a7e2f7345.png)
[LeetCode—Question 2 Sum of Two Numbers Detailed Code Explanation ] The source code is attached, which can be copied directly
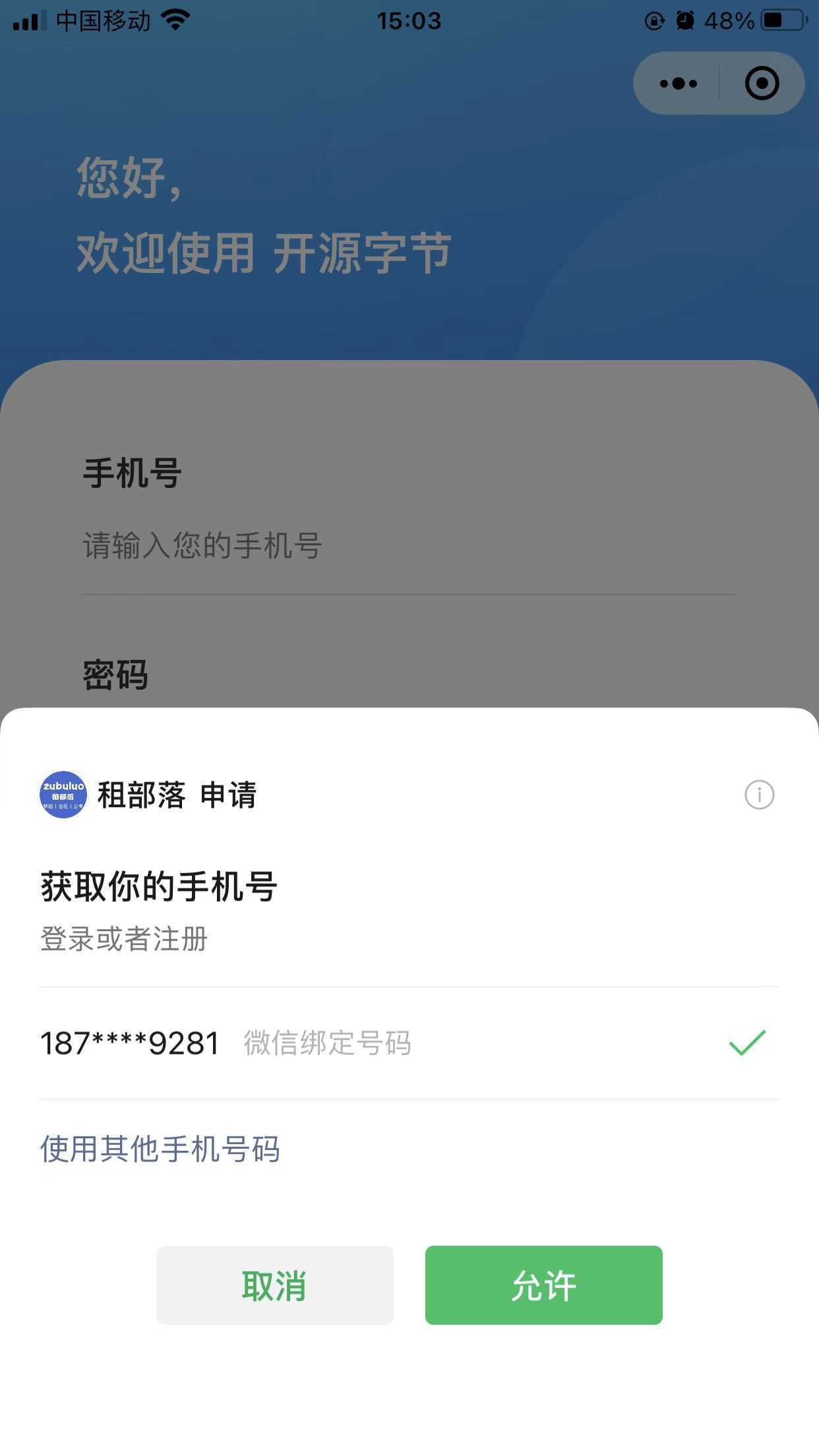
微信小程序获取用户手机号码
随机推荐
"Global Digital Economy Conference" landed in N World, Rongyun provides communication cloud service support
RTP协议分析
Question G: Word Analysis ← Questions for the second provincial competition of the 11th Blue Bridge Cup Competition
CDH6.3.2开启kerberos认证
LyScript implements memory stack scanning
矩阵的计算[通俗易懂]
「全球数字经济大会」登陆 N 世界,融云提供通信云服务支持
Classical Architecture and Memory Classification of Embedded Software Components
云原生 Dev0ps 实践
字符串本地化和消息字典(二)
智能合约是什么?
多态详细讲解(简单实现买票系统模拟,覆盖/重定义,多态原理,虚表)
直播弱网优化
【TypeScript】Why choose TypeScript?
viewstub 的详细用法_pageinfo用法
build --repot
本周四晚19:00知识赋能第4期直播丨OpenHarmony智能家居项目之设备控制实现
【冒泡排序以及奇数偶数排列】
下午见!2022京东云数据库新品发布会
微信小程序获取用户手机号码