当前位置:网站首页>最大人工岛[如何让一个连通分量的所有节点都记录总节点数?+给连通分量编号]
最大人工岛[如何让一个连通分量的所有节点都记录总节点数?+给连通分量编号]
2022-07-05 17:49:00 【REN_林森】
dfs与连通分量
前言
如何求连通分量总的所有节点数?dfs+visited
如何给连通分量的所有节点都能记录该连通分量的节点总数?将变量改为数组(大家用一个堆地址)
如何确定一个节点周围的节点是否为两个不同的连通分量?给连通分量编号 or 并查集findFather
一、最大人工岛
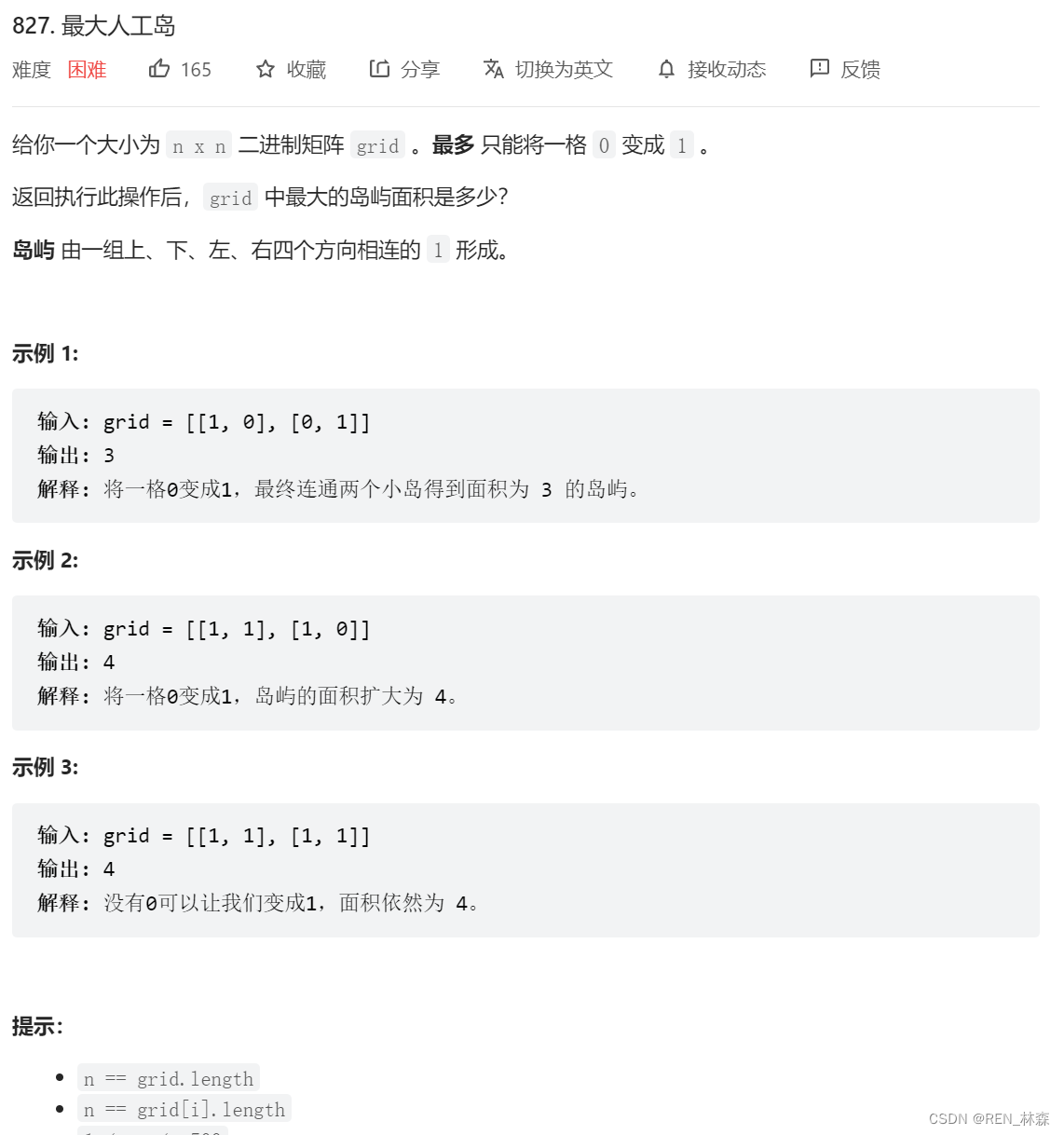
二、DFS+记搜变体
package everyday.hard;
import java.util.HashSet;
import java.util.Set;
// 最大人工岛。
public class LargestIsland {
/* target:只能将一个格子从0变为1,看最大岛屿面积。 直观:DFS求岛屿面积, 如何举一反三?既然只能让一个0变为1,那就从0的地方dfs,但是时间复杂度非常高!O(N * N * N * N) 那用空间换时间,把每个块的提前通过dfs算好,即从1的地方dfs,每个位置都记录这个连通块的总数量。 但是,这会失败,因为0的左右连通块可能不是独立的连通块,可能就是同一个连通块,则会导致重复计算。 所以,需要给连通分量块编号,不同的连通分量块才能加在一起。 */
public int largestIsland(int[][] grid) {
int m = grid.length, n = grid[0].length;
int max = 1 << 31;
int[][][] f = new int[m][n][2];
// 从1出发dfs
int idx = 0;
for (int i = 0; i < grid.length; i++) {
for (int j = 0; j < grid[0].length; j++) {
if (grid[i][j] == 1) {
int[] total = new int[]{
0, idx};
dfs(grid, i, j, f, total);
max = Math.max(max, total[0]);
++idx;
}
}
}
// 从0出发dfs。
for (int i = 0; i < grid.length; i++) {
for (int j = 0; j < grid[0].length; j++) {
if (grid[i][j] == 0) {
int total = 1;
// 去重复的连通分量
Set<Integer> bool = new HashSet<>();
for (int[] gap : gaps) {
int ni = i + gap[0], nj = j + gap[1];
if (ni == -1 || -1 == nj || nj == grid[0].length || grid.length == ni || grid[ni][nj] == 0)
continue;
if (!bool.contains(f[i][j][1])) {
total += f[i][j][0];
bool.add(f[i][j][1]);
}
}
max = Math.max(max, total);
}
}
}
return max;
}
// 方便走四个方向,采用矩阵+循环的方式。
static final int[][] gaps = new int[][]{
{
1, 0}, {
-1, 0}, {
0, 1}, {
0, -1}};
// 如何让一个连通分量的所有节点处都能赋值到总节点数。
private void dfs(int[][] grid, int i, int j, int[][][] f, int[] total) {
if (i == -1 || -1 == j || j == grid[0].length || grid.length == i || grid[i][j] <= 0) return;
total[0]++;
f[i][j] = total;
grid[i][j] = -1;
for (int[] gap : gaps) {
int ni = i + gap[0], nj = j + gap[1];
dfs(grid, ni, nj, f, total);
}
}
}
总结
1)这个题是DFS+记忆搜索的改进版本,想做的举一反三,就必须牢牢掌握其细节,如访问过的需要一直标记着,不能不标记,也不能回溯把标记去掉,这不是求最大路径值;如判定下标越界,不是i == 0 || i == n,是i == -1 || i == n,这都能搞错,服了。
2)掌握了这些基础知识,根据题目需求,来做相应的利用。比如本题可把一个0变成1,那不如就从0的地方开始遍历,取最大值。
3)今天做到这个比较丧,一直感觉思路是对的(不过思路是对的,只是有坑没发现。),花了很多时间才发现关键问题所在。(发现关键问题的能力太弱了,我觉得这是核心能力!)。但是不要气馁,看了题解,才发现这是官方故意给的坑,需要打破舒适区知识,学会举一反三,循序渐进的成长。所以想丧就要笑,大声把思路读出来,想不通就去学题解,这是突破自己的好时机。
参考文献
[1] LeetCode 最大人工岛
边栏推荐
- mybash
- Disabling and enabling inspections pycharm
- Tencent music launched its new product "quyimai", which provides music commercial copyright authorization
- Zabbix
- EasyCVR接入设备开启音频后,视频无法正常播放是什么原因?
- What are the requirements for PMP certification? How much is it?
- 使用QT遍历Json文档及搜索子对象
- Customize the theme of matrix (I) night mode
- Tkinter window preload
- Delete some elements in the array
猜你喜欢

Star ring technology data security management platform defender heavy release
解决“双击pdf文件,弹出”请安装evernote程序
Zabbix

7 pratiques devops pour améliorer la performance des applications
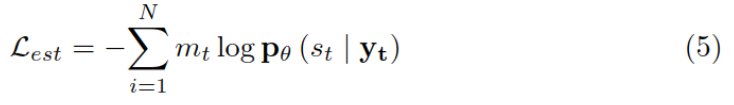
论文阅读_医疗NLP模型_ EMBERT

Ten top automation and orchestration tools

Daily exercise: a series of dates

企业数字化发展中的六个安全陋习,每一个都很危险!
mybash

星环科技数据安全管理平台 Defensor重磅发布
随机推荐
mybash
Leetcode exercise - 206 Reverse linked list
如何修改mysql字段为自增长字段
LeetCode笔记:Weekly Contest 300
怎么选择外盘期货平台最正规安全?
Teamcenter 消息注册前操作或後操作
Clickhouse (03) how to install and deploy Clickhouse
Easynmon Usage Summary
Cmake tutorial Step4 (installation and testing)
Leetcode daily question: merge two ordered arrays
企业数字化发展中的六个安全陋习,每一个都很危险!
星环科技数据安全管理平台 Defensor重磅发布
This 17-year-old hacker genius cracked the first generation iPhone!
Cmake tutorial Step2 (add Library)
每日一练:关于日期的一系列
“12306” 的架构到底有多牛逼?
Isprs2022 / Cloud Detection: Cloud Detection with Boundary nets Boundary Networks Based Cloud Detection
Redis Foundation
Sophon KG升级3.1:打破数据间壁垒,解放企业生产力
[TestLink] testlink1.9.18 solutions to common problems