St table

ST surface

Definition

· Also called RMQ Algorithm
· Given sequence , requirement O(1) Find interval （l,r） The minimum value of

·F[i][j] representative i To i+2^j-1 The minimum value of .
·F[i][j]=min(f[i][j-1],f[i+2^(j-1)][j-1])
·O(nlogn) Preprocessing

set up k Is the largest positive integer satisfying 2^k<=r-l+1 Min(l,r)=min(f[l][k],f[r-2^k+1][k]) Pictured ：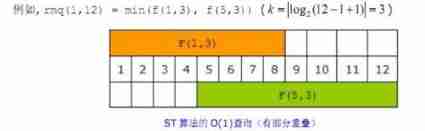

 

Board question

Luogu P3865 ST surface

Background

This is a way ST Table classic questions —— Maximum value of static interval

Please note that the maximum data time limit is only 0.8s, The data intensity is not low , Please make sure that your query complexity is O(1)O(1)O(1). If a higher time complexity algorithm is used, it is not guaranteed to pass .

If you think your code has the right time complexity, but TLE, You can try to use fast read ：

inline int read()
{
	int x=0,f=1;char ch=getchar();
	while (ch<'0'||ch>'9'){if (ch=='-') f=-1;ch=getchar();}
	while (ch>='0'&&ch<='9'){x=x*10+ch-48;ch=getchar();}
	return x*f;
}

The return value of the function is the first integer read in .

The function of fast reading is only to speed up the reading , Not mandatory .

Title Description

Given a length of NNN Sequence of numbers , and M M M Time to ask , Find out the maximum number in the interval of each query .

Input format

The first line contains two integers N,MN,MN,M, Respectively represent the length of the sequence and the number of queries .

The second line contains NNN It's an integer （ Write it down as aia_iai​）, Represent the... Of the sequence in turn iii term .

Next MMM That's ok , Each line contains two integers li,ril_i,r_ili​,ri​, Indicates that the query interval is [li,ri][l_i,r_i][li​,ri​].

Output format

The output contains MMM That's ok , One integer per row , Show the results of each inquiry in turn .

Code( very Oh Konjac ）

#include <bits/stdc++.h>
using namespace std;
const int MAXN=1e6+10;
inline int read()// Read in quickly  
{
    char c=getchar();
	int x=0,f=1;
    while(c<'0'||c>'9'){
	if(c=='-')f=-1;
	c=getchar();
}
    while(c>='0'&&c<='9'){
		x=x*10+c-'0';c=getchar();
	}
    return x*f;
}
int Max[MAXN][21];
int st(int l,int r)//ST surface  
{
    int k=log2(r-l+1); 
    return max(Max[l][k],Max[r-(1<<k)+1][k]);
}
int main(){
    int N=read(),M=read();
    for(int i=1;i<=N;i++) 
		Max[i][0]=read();
    for(int j=1;j<=21;j++)
        for(int i=1;i+(1<<j)-1<=N;i++)
            Max[i][j]=max(Max[i][j-1],Max[i+(1<<(j-1))][j-1]);
    for(int i=1;i<=M;i++)
    {
        int l=read(),r=read();
        printf("%d\n",st(l,r));
    }
    return 0;
}  

analysis

The time limit in the question is only 800ms, Time complexity is particularly important .
The last two points of this konjaku timed out
Try to use fast read

Life advice ：

Don't be too dependent cin cout The two are not a panacea , Some card time problems are easy to timeout
printf YYDS