当前位置:网站首页>2022 Hangzhou Electric Power Multi-School League Game 5 Solution
2022 Hangzhou Electric Power Multi-School League Game 5 Solution
2022-08-04 03:35:00 【Frank_Star】
比赛传送门
作者: fn
目录
签到题
1010题 Bragging Dice / “Brag dice”
题目大意
Two people play the cards “Brag dice” 游戏,Find out who wins first and second.
All the points cast by one person are not at the same time,Treated as having no points.
考察内容
博弈论
分析
When both players roll all different points,There are no points in the whole place,先手必败,否则先手必胜.
#include<bits/stdc++.h>
#define ll long long
#define cer(x) cerr<<(#x)<<" = "<<(x)<<'\n'
#define endl '\n'
using namespace std;
const int N=2e5+10;
ll n,a[N],b[N];
int main(){
ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
int t; cin>>t;
while(t--){
cin>>n;
for(int i=1;i<=n;i++){
cin>>a[i];
}
for(int i=1;i<=n;i++){
cin>>b[i];
}
int num[10]={
0};
int same=0; // The person who records the number of points
for(int i=1;i<=n;i++){
num[a[i]]++;
if(num[a[i]]>=2){
same++;
break;
}
}
memset(num,0,sizeof num);
for(int i=1;i<=n;i++){
num[b[i]]++;
if(num[b[i]]>=2){
same++;
break;
}
}
if(same>=1)cout<<"Win!"<<endl; // 至少有1Personally count
else cout<<"Just a game of chance."<<endl;
}
return 0;
}
/* 1 5 1 2 3 4 5 1 2 3 4 4 */
基本题
1012题 Buy Figurines / 买手办
题目大意
Several people line up to buy a hand,Each person chooses the queue with the least number of people in the current queue.
Ask the last person to buy the time.
考察内容
模拟,复杂度优化
分析
解法不唯一.
directly on the subject,Just simulate everyone queuing up.
When a team is available,directly in.When there are no empty teams,Updates the current headcount for all teams,Then go to the line with the smallest number of people.
#include<bits/stdc++.h>
#define ll long long
#define cer(x) cerr<<(#x)<<" = "<<(x)<<'\n'
#define endl '\n'
using namespace std;
int read(int &n){
char ch=' '; int q=0,w=1;
for(;(ch!='-')&&((ch<'0')||(ch>'9'));ch=getchar());
if(ch=='-')w=-1,ch=getchar();
for(;ch>='0'&&ch<='9';ch=getchar())q=q*10+ch-48;
n=q*w; return n;
}
ll read(ll &n){
char ch=' '; ll q=0,w=1;
for(;(ch!='-')&&((ch<'0')||(ch>'9'));ch=getchar());
if(ch=='-')w=-1,ch=getchar();
for(;ch>='0'&&ch<='9';ch=getchar())q=q*10+ch-48;
n=q*w; return n;
}
const int N=2e5+10;
ll n,m;
struct node{
ll start,last;
}a[N];
bool cmp(node x,node y){
return x.start<y.start;
}
vector<ll> v[N];
int p[N];
ll t[N]; // The last time for the team
ll num[N]; // 队伍人数
int main(){
int t0; read(t0);
while(t0--){
read(n); read(m);
for(int i=1;i<=n;i++){
read(a[i].start);
read(a[i].last);
}
sort(a+1,a+n+1,cmp); // 按照开始时间排序
memset(t,0,sizeof(t[0])*(n+1));
memset(num,0,sizeof(num[0])*(m+1));
memset(p,0,sizeof(p[0])*(m+1));
for(int i=0;i<=m;i++)v[i].clear();
for(int i=1;i<=n;i++){
// Enumerate each one
int F=0;
for(int j=1;j<=m;j++){
// Enumerate each team
if(a[i].start>=t[j]){
// can go directly in
F=1;
t[j]=a[i].start+a[i].last;
v[j].push_back(t[j]);
num[j]++;
break;
}
}
if(F){
continue;
}
// When you can't find a team without people
for(int j=1;j<=m;j++){
// Enumerate each team,更新num[j]
int len=v[j].size();
for(int k=p[j];k<len;k++){
if(v[j][k]<=a[i].start){
p[j]++;
num[j]--;
}
else{
break;
}
}
}
ll minnum=1e18; // Find the minimum number of teams
for(int j=1;j<=m;j++){
minnum=min(minnum,num[j]);
}
for(int j=1;j<=m;j++){
if(num[j]==minnum){
// 人数最少
t[j]+=a[i].last;
v[j].push_back(t[j]);
num[j]++;
break;
}
}
}
ll ans=0;
for(int i=1;i<=m;i++){
ans=max(ans,t[i]);
}
cout<<ans<<endl;
}
return 0;
}
1003题 Slipper / 拖鞋
题目大意
Given a tree and the weight of the top of the tree,Every time you can walk the edge of the tree,也可以花费 p p p The cost jumps up or down k k k 层.求点 s s s 到点 t t t 的最短路.
考察内容
树形dp,dfs,最短路
分析
I wrote one at the time of the gamedijkstra然后tle了,So I wrote a treedp.
Set a state for each point and each layer,Then start from the enddfsJust transfer it.
状态:
f [ i ] f[i] f[i] 表示第 i i i The shortest distance from a node to an end point.
f 2 [ i ] f2[i] f2[i] 表示第 i i i 层中"最好"The shortest distance from the point to the end point.
转移:
对于每个结点,Enumerates all out-edges and jumps up and down,更新答案.
This method does not add extra edges,Each node is enumerated at most once during transition,复杂度 O ( n ) O(n) O(n)
#pragma GCC optimize(3) // O3优化
#include<bits/stdc++.h>
#define ll long long
#define cer(x) cerr<<(#x)<<" = "<<(x)<<'\n'
#define endl '\n'
using namespace std;
int read(int &n){
char ch=' '; int q=0,w=1;
for(;(ch!='-')&&((ch<'0')||(ch>'9'));ch=getchar());
if(ch=='-')w=-1,ch=getchar();
for(;ch>='0'&&ch<='9';ch=getchar())q=q*10+ch-48;
n=q*w; return n;
}
ll read(ll &n){
char ch=' '; ll q=0,w=1;
for(;(ch!='-')&&((ch<'0')||(ch>'9'));ch=getchar());
if(ch=='-')w=-1,ch=getchar();
for(;ch>='0'&&ch<='9';ch=getchar())q=q*10+ch-48;
n=q*w; return n;
}
const int N=1e6+5;
const int M=1e6+5;
int head[N];
int ver[M],edge[M],nxt[M];
bool vis[N];
ll n,tot;
ll k,p,s,t;
ll u[N],v[N],w[N];
ll deep[N];
vector<ll> g[N];
ll f[N]; // f[i]表示第iThe shortest distance from a node to an end point
ll f2[N]; // f2[i]表示第i层中"最好"The shortest distance from the point to the end point
ll maxd=0;
void add(int x,int y,int z){
ver[++tot]=y;
edge[tot]=z; // 记录边权
nxt[tot]=head[x];
head[x]=tot;
}
void dfs(int v,int fa,int d1){
// Mark the node depth
deep[v]=d1;
for(auto a1:g[v]){
if(a1==fa)continue;
dfs(a1,v,d1+1);
}
}
void dfs2(int v){
if(vis[v])return;
vis[v]=1;
int x=v;
for(int i=head[x];i>0;i=nxt[i]){
// enumerate out edges
int y=ver[i];
int z=edge[i]; // zSave edge rights
if(abs(deep[x]-deep[y])==k){
// 可以跳
z=min((ll)z,p); // 更新z
}
if(f[y]>f[x]+z){
f[y]=f[x]+z; // 转移
}
if(deep[y]+k<=maxd){
f[y]=min(f[y],f2[deep[y]+k]+p); // 转移
f2[deep[y]]=min(f2[deep[y]],f[y]);
}
if(deep[y]-k>=1){
f[y]=min(f[y],f2[deep[y]-k]+p); // 转移
f2[deep[y]]=min(f2[deep[y]],f[y]);
}
dfs2(y);
}
}
struct node{
ll deep,id;
}n1[N];
bool cmp(node nx,node ny){
return nx.deep<ny.deep;
}
void init(ll n){
// 初始化
memset(head,0,sizeof(head[0])*(n+1));
memset(vis,0,sizeof(vis[0])*(n+1));
memset(deep,0,sizeof(deep[0])*(n+1));
memset(ver,0,sizeof ver);
memset(edge,0,sizeof edge);
memset(nxt,0,sizeof nxt);
tot=0;
for(int i=0;i<=n;i++){
g[i].clear();
}
}
int main(){
// 树形dp
int t0; read(t0);
while(t0--){
read(n);
for(int i=1;i<=n-1;i++){
read(u[i]);
read(v[i]);
read(w[i]);
}
read(k); read(p); // 可以花费pThe skip depth gap is k的结点
read(s); read(t);
init(n); // 初始化
for(int i=1;i<=n-1;i++){
add(u[i],v[i],w[i]);
add(v[i],u[i],w[i]);
g[u[i]].push_back(v[i]);
g[v[i]].push_back(u[i]);
}
dfs(1,0,1); // 从根结点开始,Mark the depth of each node
for(int i=0;i<=n;i++){
f[i]=f2[i]=1e18;
}
f[t]=0; // The distance from the end point to yourself0
maxd=deep[1]; // 保存最大深度
for(int i=2;i<=n;i++){
maxd=max(maxd,deep[i]);
}
f2[deep[t]]=0;
// The point at which the transition and the end point are directly connected
int x=t;
for(int i=head[x];i>0;i=nxt[i]){
int y=ver[i];
int z=edge[i]; // zSave edge rights
if(f[y]>f[x]+z){
f[y]=f[x]+z;
f2[deep[y]]=min(f2[deep[y]],f[y]);
}
}
for(int i=max(k,t+1);i<=maxd;i++){
f2[i]=min(f2[i],f2[i-k]+p); // 更新f2[]
}
for(int i=t-1;i>=1;i--){
f2[i]=min(f2[i],f2[i+k]+p); // 更新f2[]
}
dfs2(t); // 转移
cout<<f[s]<<endl; // The answer is the shortest distance from the start point to the end point
}
return 0;
}
/* 1 11 1 2 10 2 3 10 1 4 10 4 5 10 1 6 10 6 7 10 1 8 10 8 9 10 1 10 10 10 11 10 1 2 3 11 */
进阶题
1007题 Count Set / 数集合
题目大意
从一个 1 1 1 到 n n n selection in the arrangement k k k 个数字,Requires that each selected number and all selected subscripts be different.
求选择的方案数.
考察内容
生成函数,NTT,数学知识,Pólya定理
分析

#include<bits/stdc++.h>
#define fr(i,l) for(S i=0;i<l;i++)
#define S int
#define U unsigned
#define UL U long long
#define LL long long
constexpr U mod=998244353u;
constexpr U g=3u;
constexpr U gi=332748118u;
using std::max;
using std::min;
using std::swap;
U pow(U a,U b)
{
U ans=1;
while(b)
{
if(b&1)ans=(UL)ans*a%mod;
a=(UL)a*a%mod;
b>>=1;
}
return ans;
}
U mo(U x){
return x>=mod?x-mod:x;}
U& mul(U&a,U b){
return a=(UL)a*b%mod;}
void mov(U*a,const U*b,S len){
memmove(a,b,len*sizeof(U));}
namespace Poly
{
constexpr S ml=1<<19,mn=80;
U mem[(ml+16)*mn],*stk[mn],top=mn,f[(ml+16)*2],wr[ml+16],wi[ml+16],ninv[ml+16];
U*m(){
return stk[--top];}void m(U*p){
stk[top++]=p;}
S up(S x){
S l=1;while(l<x)l<<=1;return l;}
void init()
{
fr(i,mn)stk[i]=mem+i*(ml+16);
U*fp;
for(S len=1;fp=f+len,len<=ml;len<<=1)
fr(i,len)fp[i]=(fp[i>>1]>>1)|(i&1?len>>1:0);
for(S len=1;len<ml;len<<=1)
{
U Wr=pow(g,(mod-1)/(len<<1));
U Wi=pow(gi,(mod-1)/(len<<1));
U tr=1,ti=1;
fr(i,len)
{
wr[len+i]=tr;mul(tr,Wr);
wi[len+i]=ti;mul(ti,Wi);
}
}
}
#define lst(n,a,x) poly&n(a){
x return*this;}
struct poly{
U*mem,*a;
S len;
poly(S len):len(len){
a=mem=m();cls(0,len);}
poly():poly(1){
}
poly(U x):poly(){
a[0]=x;}
poly(U*l,S len):len(len){
a=mem=m();mov(a,l,len);}
poly(const poly&b):poly(b.a,b.len){
}
~poly(){
if(mem)m(mem);}
lst(operator=,const poly&b,if(mem)rsz(b.len);mov(a,b.a,b.len);)
U& operator[](S idx){
return a[idx];}
poly& cls(S l,S len){
memset(a+l,0,len*4);return *this;}
lst(rsz,S nlen,if(nlen>len)cls(len,nlen-len);len=nlen;)
template<U*wp=wr>
lst(NTT,S len=-1,static UL a[ml+16];
if(~len)rsz(len);else len=this->len;
fr(i,len)a[i]=this->a[f[len+i]];
for(S i=1;i<len;i<<=1)
{
U*w=wp+i;
for(S j=0;j<len;j+=i<<1)
fr(k,i)
{
UL x=a[j+k];
UL y=a[i+j+k]*w[k]%mod;
a[j+k]=x+y;
a[i+j+k]=x-y+mod;
}
}
fr(i,len)this->a[i]=a[i]%mod;
)
lst(NTTi,S len=-1,NTT<wi>(len);*this*=pow(this->len,mod-2);)
poly operator+(const poly&b){
return poly(*this)+=b;}
poly operator-(const poly&b){
return poly(*this)-=b;}
poly operator*(const poly&b){
return poly(*this)*=b;}
poly operator*(U x){
return poly(*this)*=x;}
lst(operator+=,const poly&b,rsz(max(len,b.len));fr(i,b.len)a[i]=mo(a[i]+b.a[i]);)
lst(operator-=,const poly&b,rsz(max(len,b.len));fr(i,b.len)a[i]=mo(a[i]-b.a[i]+mod);)
lst(operator*=,poly b,S l=up(len+b.len-1);NTT(l).vmul(b.NTT(l)).NTTi();)
lst(operator*=,U x,fr(i,len)mul(a[i],x);)
lst(vmul,const poly&b,fr(i,len)mul(a[i],b.a[i]);)
lst(print,,fr(i,len)printf("%u ",a[i]);puts("");)
};
};
using Poly::poly;
U fact[500001];
U ifact[500001];
U C(int n,int m){
if(m<0||m>n)return 0;
return (UL)fact[n]*ifact[m]%mod*ifact[n-m]%mod;
}
int p[500000];
int vis[500000];
int sz[500000],num;
poly calc(int l,int r){
if(l==r){
poly t(sz[l]/2+1);
t[0]=1;
for(S i=1;i<t.len;i++)
t[i]=mo(C(sz[l]-i-1,i-1)+C(sz[l]-i,i));
return t;
}
else{
int mid=l+r>>1;
poly a=calc(l,mid);
poly b=calc(mid+1,r);
int len=a.len+b.len-1;
return (a*=b).rsz(len);
}
}
void sol(){
int n,k;
scanf("%d%d",&n,&k);
fr(i,n)scanf("%d",p+i),p[i]--;
memset(vis,0,4*n);
num=0;
fr(i,n){
if(!vis[i]){
vis[i]=1;
sz[num]=1;
int t=p[i];
while(!vis[t]){
vis[t]=1;
sz[num]++;
t=p[t];
}
if(sz[num]>1)num++;
}
}
poly a=calc(0,num-1);
if(k>=a.len){
printf("0\n");
}
else{
printf("%u\n",a[k]);
}
}
int main(){
Poly::init();
// 预处理阶乘
fact[0]=1;
for(S i=1;i<=500000;i++)
fact[i]=(UL)fact[i-1]*i%mod;
ifact[500000]=pow(fact[500000],mod-2);
for(S i=500000;i;i--)
ifact[i-1]=(UL)ifact[i]*i%mod;
int T;
scanf("%d",&T);
while(T--)sol();
}
边栏推荐
- FFmpeg —— 通过修改yuv,将视频转为黑白并输出(附源码)
- JVM内存和垃圾回收-07.堆
- 创新互融|华秋赋能助力OpenHarmony生态硬件开发落地
- STM8S项目创建(STVD创建)---使用 COSMIC 创建 C 语言项目
- Based on the statistical QDirStat Qt directory
- Why use Selenium for automated testing
- 多线程间的通信方式你知道几种?
- 4-way two-way HDMI integrated business high-definition video optical transceiver 8-way HDMI high-definition video optical transceiver
- docker+网桥+redis主从+哨兵模式
- 复制带随机指针的链表
猜你喜欢
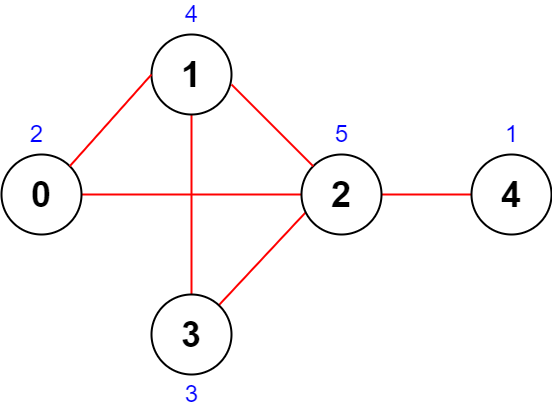
LeetCode每日一题(2285. Maximum Total Importance of Roads)
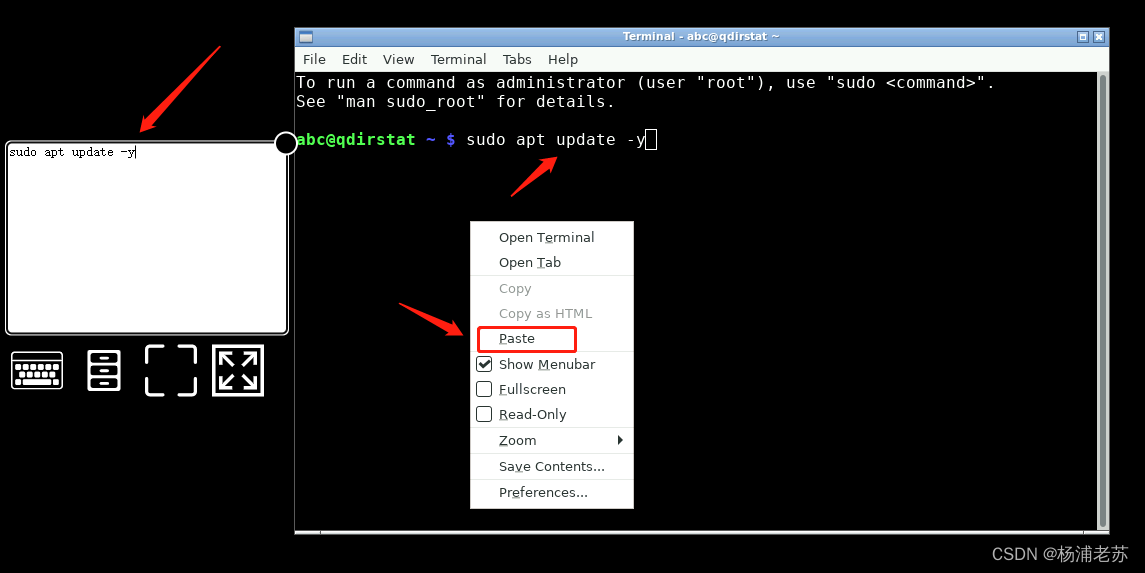
Based on the statistical QDirStat Qt directory
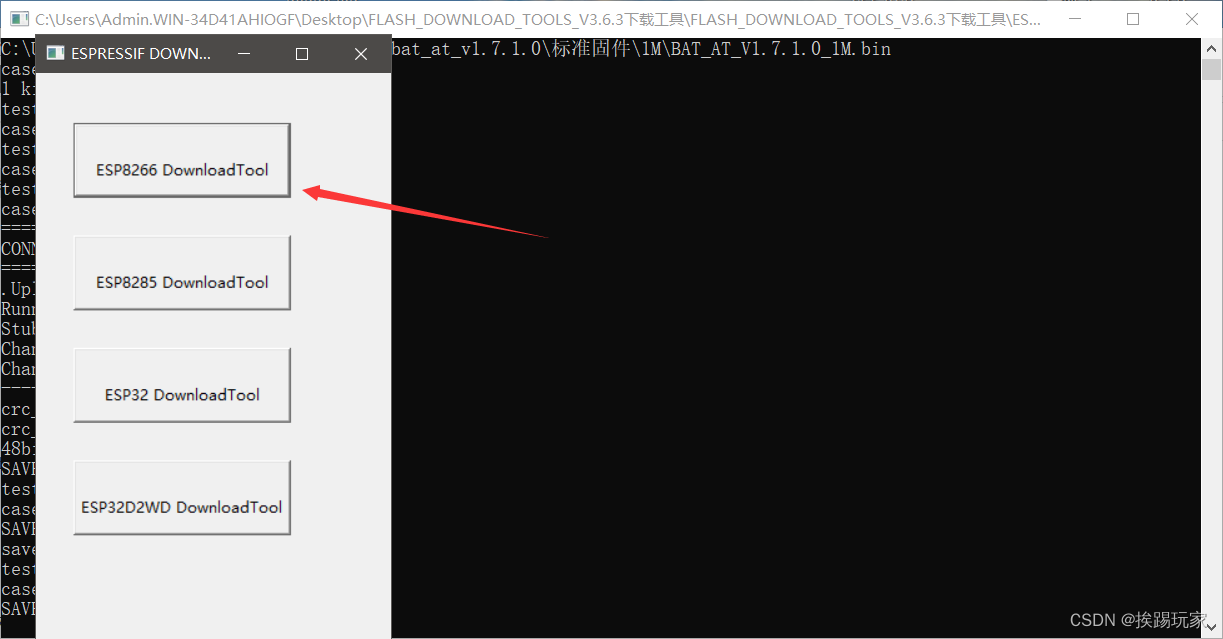
Brush esp8266-01 s firmware steps
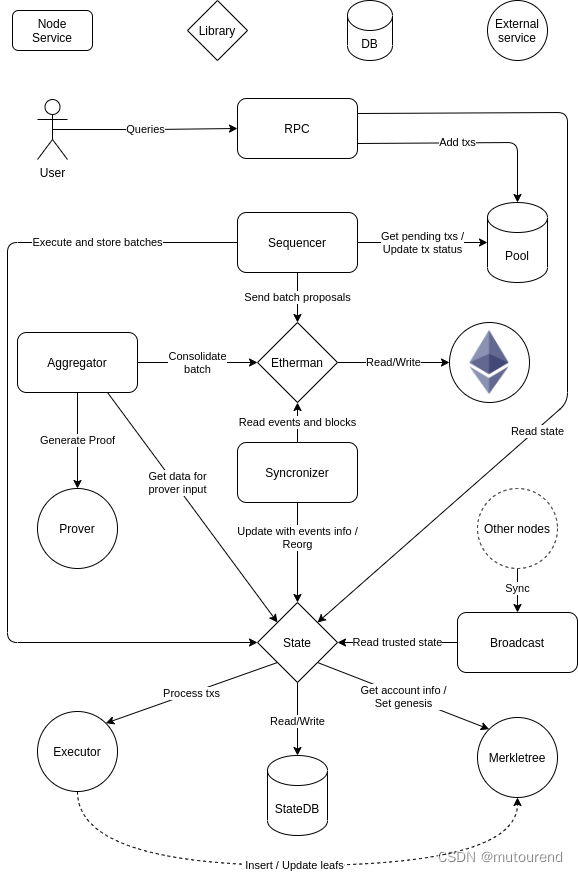
Polygon zkEVM network node
new Date converts strings into date formats Compatible with IE, how ie8 converts strings into date formats through new Date, how to replace strings in js, and explain the replace() method in detail
SQL injection in #, - +, - % 20, % 23 is what mean?
Basic form validation process

mq应用场景介绍

一个属于程序员的七夕节!

【医保科普】维护医保基金安全,我们可以这样做
随机推荐
异步编程解决方案 Generator生成器函数、iterator迭代器、async/await、Promise
《nlp入门+实战:第八章:使用Pytorch实现手写数字识别》
ingress 待完善
函数,递归以及dom简单操作
pnpm 是凭什么对 npm 和 yarn 降维打击的
DIY电工维修如何拆卸和安装开关面板插座
How many ways do you know about communication between multiple threads?
MySQL Query Exercise (1)
MySQL query optimization and tuning
new Date将字符串转化成日期格式 兼容IE,ie8如何通过new Date将字符串转化成日期格式,js中如何进行字符串替换, replace() 方法详解
逻辑漏洞----其他类型
Architecture of the actual combat camp module three operations
安装postgis时报找不到“POSTGIS_VERSION”这个函数
怎样提高网络数据安全性
STM8S105k4t6c---------------Light up LED
返回字符串中的最大回文数
Homemade bluetooth mobile app to control stm8/stm32/C51 onboard LED
帮助企业实现数字化转型成功的八项指导原则
Why use Selenium for automated testing
【医保科普】维护医保基金安全,我们可以这样做