codeforces每日5题(均1600)-第二十八天

Ivan and Powers of Two

题面翻译

有一个由 $n$ 个非负整数组成的序列 $a_1$ 到
$a_n$，这个序列保证单调不降。接着，小华将上述序列作为2的次幂，写下了另一个序列：2的 $a_1$ 次幂到2的 $a_n$ 次幂。
现在他想知道，最少要在这个序列中添加多少个形式为 $2^x$ 的数（$x$ 为非负整数），才能使这个序列所有整数的和为 $2^v-1$，其中 $v$ 为某个非负整数。

题目描述

Ivan has got an array of $n$ non-negative integers $a_1,a_2,...,a_n$ .

Ivan knows that the array is sorted in the non-decreasing order.

Ivan wrote out integers $2^{a_1},2^{a_2},...,2^{a_n}$ on a piece of paper.

Now he wonders, what minimum number of integers of form $2^b$$(b>=0)$ need to be added to the piece of paper so that the sum of all integers written on the paper equalled $2^v-1$ for some integer $v$$(v>=0)$ .

Help Ivan, find the required quantity of numbers.

输入格式

The first line contains integer $n$ ( $1<=n<=10^5$ ).

The second input line contains $n$ space-separated integers $a_1,a_2,...,a_n$$(0<=a_i<=2\cdot 10^9)$ .

It is guaranteed that $a_1<=a_2<=...<=a_n$ .

输出格式

Print a single integer — the answer to the problem.

样例 #1

样例输入 #1

4
0 1 1 1

样例输出 #1

0

样例 #2

样例输入 #2

1
3

样例输出 #2

3

提示

In the first sample you do not need to add anything, the sum of numbers already equals $2^3-1=7$ .

In the second sample you need to add numbers $2^0,2^1,2^2$ .

#include<bits/stdc++.h>
using namespace std;
const int N=2e6+10;
typedef long long ll;
int n,v,ans,x;
map<int,int>sum;
int main(){
    
	cin>>n; 
	for(int i=1;i<=n;++i){
    
		cin>>x;
		while(sum.count(x))
			sum.erase(x++);
		++sum[x];
		v=max(v,x);
	}
	cout<<v+1-sum.size()<<endl;
	return 0;
}

Perfect Pair

题面翻译

题目大意：定义一对数(x,y)，若x、y中至少有一个大于等于m，则称(x,y)对m完美。

现在给定一对数(x,y)，允许把其中的一个数换成x+y，问把(x,y)变成对m完美的数对至少需要几次操作。

题目描述

Let us call a pair of integer numbers $m$ -perfect, if at least one number in the pair is greater than or equal to $m$ .

Thus, the pairs (3, 3) and (0, 2) are 2-perfect while the pair (-1, 1) is not.

Two integers $x$ , $y$ are written on the blackboard.

It is allowed to erase one of them and replace it with the sum of the numbers, $(x+y)$ .

What is the minimum number of such operations one has to perform in order to make the given pair of integers $m$ -perfect?

输入格式

Single line of the input contains three integers $x$ , $y$ and $m$ ( $-10^{18}<=x$ , $y$ , $m<=10^{18}$ ).

Please, do not use the %lld specifier to read or write 64-bit integers in C++. It is preffered to use the cin, cout streams or the %I64d specifier.

输出格式

Print the minimum number of operations or “-1” (without quotes), if it is impossible to transform the given pair to the $m$ -perfect one.

样例 #1

样例输入 #1

1 2 5

样例输出 #1

2

样例 #2

样例输入 #2

-1 4 15

样例输出 #2

4

样例 #3

样例输入 #3

0 -1 5

样例输出 #3

-1

提示

In the first sample the following sequence of operations is suitable: (1, 2) (3, 2) (5, 2).

In the second sample: (-1, 4) (3, 4) (7, 4) (11, 4) (15, 4).

Finally, in the third sample $x$ , $y$ cannot be made positive, hence there is no proper sequence of operations.

#include<bits/stdc++.h>
using namespace std;
const int N=2e6+10;
typedef long long ll;
ll x,y,m,s=0;
int main(){
    
	cin>>x>>y>>m; 
	if(x>=m||y>=m){
    
		puts("0");
		return 0;
	}
	else if(x<=0&&y<=0){
    
		puts("-1");
		return 0;
	}
	else if(x*y<0){
    
		if(x<y){
    
			s+=(-x)/y;
			x=x%y;
		}
		else{
    
			s+=(-y)/x;
			y=y%x;
		}
	}
	while(x<m&&y<m){
    
		if(x>y)swap(x,y);
		x+=y;
		s++;
	}
	cout<<s;
	return 0;
}

Ciel and Flowers

题面翻译

Fox Ciel有r朵红花，g朵绿花和b朵蓝花。她想用这些花做几个花束。

有四种类型的花束：

• 制作“红色花束”，要3朵红花
• 制作“绿色花束”，要3朵绿花
• 制作“蓝色花束”，要3朵蓝花
• 制作“混合花束”，要1朵红，1朵绿和1朵蓝花

输出可以制作的最大数量的花束。

题目描述

Fox Ciel has some flowers: $r$ red flowers, $g$ green flowers and $b$ blue flowers.

She wants to use these flowers to make several bouquets.

There are 4 types of bouquets:

• To make a “red bouquet”, it needs 3 red flowers.
• To make a “green bouquet”, it needs 3 green flowers.
• To make a “blue bouquet”, it needs 3 blue flowers.
• To make a “mixing bouquet”, it needs 1 red, 1 green and 1 blue flower.

Help Fox Ciel to find the maximal number of bouquets she can make.

输入格式

The first line contains three integers $r$ , $g$ and $b$ ( $0<=r,g,b<=10^9$ ) — the number of red, green and blue flowers.

输出格式

Print the maximal number of bouquets Fox Ciel can make.

样例 #1

样例输入 #1

3 6 9

样例输出 #1

6

样例 #2

样例输入 #2

4 4 4

样例输出 #2

4

样例 #3

样例输入 #3

0 0 0

样例输出 #3

0

提示

In test case 1, we can make 1 red bouquet, 2 green bouquets and 3 blue bouquets.

In test case 2, we can make 1 red, 1 green, 1 blue and 1 mixing bouquet.

#include<bits/stdc++.h>
using namespace std;
const int N=2e6+10;
typedef long long ll;
ll a,b,c,ans;
int main(){
    
	cin>>a>>b>>c;
	ans=a/3+b/3+c/3+min(a%3,min(b%3,c%3));
	if(a>=1&&b>=1&&c>=1) ans=max(ans,(a-1)/3+(b-1)/3+(c-1)/3+1+min((a+2)%3,min((b+2)%3,(c+2)%3)));
	if(a>=2&&b>=2&&c>=2) ans=max(ans,(a-2)/3+(b-2)/3+(c-2)/3+2+min((a+1)%3,min((b+1)%3,(c+1)%3)));
	printf("%d\n",ans);
	return 0;
}

Secrets

题面翻译

这个世界上只有这样面值的硬币：1,3,9,27,81,…有一个商人，某一天遇到了一个顾客，他购买了价值n的商品，发现用自己的硬币无法付给商人刚好n的钱。那个顾客会给商人大于等于n的钱且使得给商人的硬币数量最少。

在这个顾客有的硬币可能的各种情况下，请问这个商人最多可能收到多少硬币？

题目描述

Gerald has been selling state secrets at leisure.

All the secrets cost the same: $n$ marks.

The state which secrets Gerald is selling, has no paper money, only coins.

But there are coins of all positive integer denominations that are powers of three: 1 mark, 3 marks, 9 marks, 27 marks and so on.

There are no coins of other denominations.

Of course, Gerald likes it when he gets money without the change.

And all buyers respect him and try to give the desired sum without change, if possible.

But this does not always happen.

One day an unlucky buyer came.

He did not have the desired sum without change.

Then he took out all his coins and tried to give Gerald a larger than necessary sum with as few coins as possible.

What is the maximum number of coins he could get?

The formal explanation of the previous paragraph: we consider all the possible combinations of coins for which the buyer can not give Gerald the sum of $n$ marks without change.

For each such combination calculate the minimum number of coins that can bring the buyer at least $n$ marks.

Among all combinations choose the maximum of the minimum number of coins. This is the number we want.

输入格式

The single line contains a single integer $n$ ( $1<=n<=10^{17}$ ).

Please, do not use the %lld specifier to read or write 64 bit integers in С++. It is preferred to use the cin, cout streams or the %I64d specifier.

输出格式

In a single line print an integer: the maximum number of coins the unlucky buyer could have paid with.

样例 #1

样例输入 #1

1

样例输出 #1

1

样例 #2

样例输入 #2

4

样例输出 #2

2

提示

In the first test case, if a buyer has exactly one coin of at least 3 marks, then, to give Gerald one mark, he will have to give this coin.

In this sample, the customer can not have a coin of one mark, as in this case, he will be able to give the money to Gerald without any change.

In the second test case, if the buyer had exactly three coins of 3 marks, then, to give Gerald 4 marks, he will have to give two of these coins.

The buyer cannot give three coins as he wants to minimize the number of coins that he gives.

#include<bits/stdc++.h>
using namespace std;
const int N=2e6+10;
typedef long long ll;
ll n,s=1;
int main(){
    
	cin>>n;
	while(n%s==0) s*=3;
	cout<<n/s+1;
	return 0;
}

Rational Resistance

题面翻译

题意翻译简化:

迈克有许多阻值为 $1\Omega$ 的电阻，通过串联、并联的方式组装为一个电阻为 $\frac{a}{b}$ 的元件，求所需的最少电阻数量。

数据:

$1<=a,b<=10^{18}$，保证 $\frac{a}{b}$ 已经最简，保证有解。

题目描述

Mad scientist Mike is building a time machine in his spare time.

To finish the work, he needs a resistor with a certain resistance value.

However, all Mike has is lots of identical resistors with unit resistance $R_0=1$ .

Elements with other resistance can be constructed from these resistors.

In this problem, we will consider the following as elements:

1. one resistor;
2. an element and one resistor plugged in sequence;
3. an element and one resistor plugged in parallel.

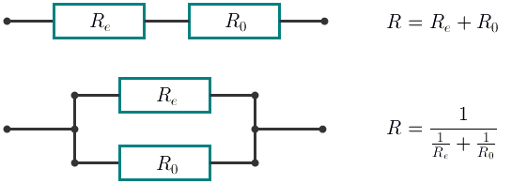With the consecutive connection the resistance of the new element equals $R=R_e+R_0$ .
With the parallel connection the resistance of the new element equals 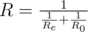. In this case $R_e$ equals the resistance of the element being connected.

Mike needs to assemble an element with a resistance equal to the fraction .

Determine the smallest possible number of resistors he needs to make such an element.

输入格式

The single input line contains two space-separated integers $a$ and $b$ ( $1<=a,b<=10^{18}$ ).

It is guaranteed that the fraction is irreducible. It is guaranteed that a solution always exists.

输出格式

Print a single number — the answer to the problem.

Please do not use the %lld specifier to read or write 64-bit integers in С++. It is recommended to use the cin, cout streams or the %I64d specifier.

样例 #1

样例输入 #1

1 1

样例输出 #1

1

样例 #2

样例输入 #2

3 2

样例输出 #2

3

样例 #3

样例输入 #3

199 200

样例输出 #3

200

提示

In the first sample, one resistor is enough.

In the second sample one can connect the resistors in parallel, take the resulting element and connect it to a third resistor consecutively.

Then, we get an element with resistance 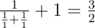. We cannot make this element using two resistors.

#include<bits/stdc++.h>
using namespace std;
const int N=2e6+10;
typedef long long ll;
ll a,b,c,s=0;
int main(){
    
	cin>>a>>b;
	while(b!=0){
    
		s+=a/b;
		c=a%b;
		a=b,b=c;
	}
	cout<<s;
	return 0;
}