当前位置:网站首页>"Torch" tensor multiplication: matmul, einsum
"Torch" tensor multiplication: matmul, einsum
2022-08-01 20:01:00 【panbaoran913】
参考博文:《张量相乘matmul函数》
一、torch.matmul
matmul(input, other, out = None) 函数对 input 和 other Matrix multiplication of two tensors.torch.matmul The function has many overloaded functions depending on the tensor dimension of the passed arguments.
When multiplying tensors,并不是标准的 ( m , n ) × ( n , l ) = ( m , l ) (m,n) \times (n,l) =(m,l) (m,n)×(n,l)=(m,l)的形式.
三、1D and 2D multiplication
3.1 1D multiplied by 2D: ( m ) × ( m , n ) = ( n ) (m) \times (m,n)=(n) (m)×(m,n)=(n)
A1 =torch.FloatTensor(size=(4,))
A2=torch.FloatTensor(size=(4,3))
A12=torch.matmul(A1,A2)
A12.shape # (3,)
3.2 Two-dimensional by one-dimensional: ( m , n ) ∗ ( n ) = ( m ) (m,n)*(n)=(m) (m,n)∗(n)=(m)
A3=torch.FloatTensor(size=(3,4))
A31=torch.matmul(A3,A1)
A31.shape #(3,)
四、Multiply 2D and 3D
4.1 2D multiplication3维: ( m , n ) × ( b , n , l ) = ( b , m , l ) (m,n)\times (b, n, l)=(b, m, l) (m,n)×(b,n,l)=(b,m,l).The expansion plan is ( b , m , n ) × ( b , n , l ) = ( b , m , l ) (b, m,n)\times (b, n,l) =(b, m,l) (b,m,n)×(b,n,l)=(b,m,l)
B1=torch.FloatTensor(size=(2,3))
B2=torch.FloatTensor(size=(5,3,4))
B12=torch.matmul(B1,B2)
B12.shape #(5,2,4)
等价方案:
B12_=torch.einsum("ij,bjk->bik",B1,B2)
torch.sum(B12==B12_)#40=2*4*5
4.2 3D times 2D: ( b , m , n ) × ( n , l ) = ( b , m , l ) (b, m, n)\times (n,l)=(b, m,l) (b,m,n)×(n,l)=(b,m,l).
B2=torch.FloatTensor(size=(5,3,4))
B3=torch.FloatTensor(size=(4,2))
B23=torch.matmul(B2,B3)
B23.shape #(5,3,2)
等价方案:
BB23_ =torch.einsum("bij,jk->bik",[B2,B3])
BB23_.shape #(5,3,2)
torch.sum(B23==BB23_)#30=5*3*2
4. 3 Two-dimensional expansion into three-dimensional way
方式一:The first tensor is expanded from two dimensions to three dimensions
B1(2,3)–>B1_(5,2,3)
B1=torch.FloatTensor(size=(2,3))
B1_ =torch.unsqueeze(B1,axis=0) #升维
print(B1_.shape) #torch.Size([1, 2, 3])
B11 =torch.cat([B1_,B1_,B1_,B1_,B1_],axis=0)#合并-->扩维
print(B11.shape) #torch.Size([5, 2, 3])
比较 B 1 ( 2 , 3 ) × B 2 ( 5 , 3 , 4 ) 与 B 11 ( 5 , 2 , 3 ) × B 2 ( 5 , 3 , 4 ) B1(2,3)\times B2(5,3,4)与B11(5,2,3)\times B2(5,3,4) B1(2,3)×B2(5,3,4)与B11(5,2,3)×B2(5,3,4)的结果
B112=torch.matmul(B11,B2)#(5,2,3)*(5,3,4)
torch.sum(B112==B12)#40=5*2*3
Indicates that both values are exactly the same.Let's further explore the mechanism of its multiplication.
我们拿B1(2,3)与B2(5,3,4)Multiply the first matrix in ,to see if it is equal to the first matrix in . The following proofs are equivalent
B12_0=torch.matmul(B1,B2[0])
B112[0]==B12_[0]
out:
tensor([[True, True, True, True],
[True, True, True, True]])
2Dimension multiplied by3Dimensional Matrix Demonstration Diagram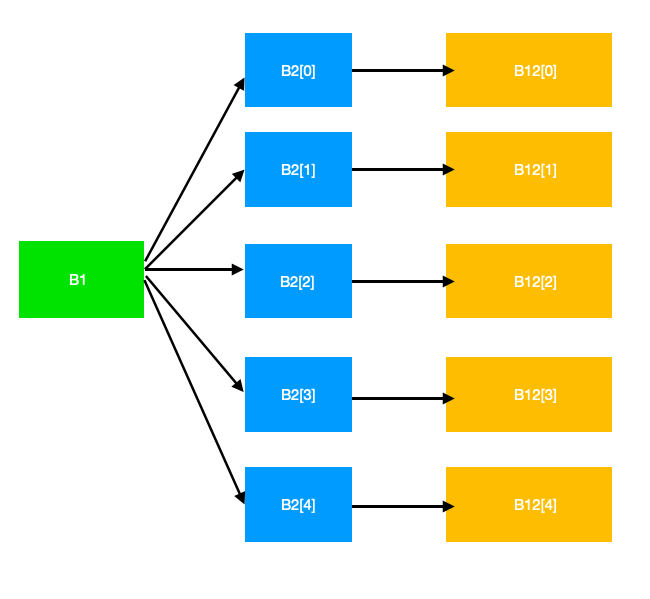
方式二:The second tensor is expanded from two dimensions to three dimensions
B3(4,2)–>B3_(5, 4, 2)
B3_=torch.unsqueeze(B3,axis=0)
print(B3_.shape)#(1,4,2)
B33 =torch.cat([B3_,B3_,B3_,B3_,B3_],axis=0)
print(B33.shape)#(5,4,2)
B233 =torch.matmul(B2,B33)
print(B233.shape) #(5,3,2)
Compare the results of the two multiplications:
print(torch.sum(B233==B23_)) #30
print(torch.sum(B233==B23)) #30
提醒:torch的FloatTensor中出现了nan值,seems to be unequal.
五、Multiply 2D and 4D
5.1 Two-dimensional by four-dimensional: ( m , n ) × ( b , c , n , l ) = ( b , c , m , l ) (m,n)\times (b,c,n,l) =(b,c,m,l) (m,n)×(b,c,n,l)=(b,c,m,l)
B1=torch.FloatTensor(size=(2,3))
B4 =torch.FloatTensor(size=(7,5,3,4))
B14 =torch.matmul(B1,B4)
print(B14.shape) #(7, 5, 2, 4)
等价方案
B14_= torch.einsum("mn,bcnl->bcml",[B1,B4])
print(torch.sum(B14==B14_))#280=7*5*2*4
升维
## 升维
B11 = torch.unsqueeze(B1,dim=0)
B11 = torch.concat([B11,B11,B11,B11,B11],dim=0)
print(B11.shape)#(5,2,3)
B111 = torch.unsqueeze(B11,dim=0)
B111 =torch.concat([B111,B111,B111,B111,B111,B111,B111],dim = 0)
print(B111.shape)#(7,5,2,3)
广播后的4Dimension multiplied by4维
B1114 = torch.matmul(B111,B4)
print(B1114.shape)#(7,5,3,4)
print(torch.sum(B1114==B14))#280
5.2 Four dimensions multiplied by two dimensions: ( b , c , n , l ) × ( l , p ) = ( b , c , n , p ) (b,c,n,l) \times (l,p)= (b,c,n,p) (b,c,n,l)×(l,p)=(b,c,n,p)
4Dimension multiplied by2维
B43 = torch.matmul(B4,B3)
print("B43 shape",B43.shape) #(7,5,3,2)
等价形式
B43_ = torch.einsum("bcnl,lp->bcnp",[B4,B3])
print("B4 is nan",torch.sum(B4.isnan()))#0
print(torch.sum(B43==B43_))#210 =7*5*3*2
升维
B33 =torch.unsqueeze(B3,dim=0)
B33 = torch.concat([B33,B33,B33,B33,B33],dim =0)
B333 = torch.unsqueeze(B33,dim =0)
B333 =torch.concat([B333,B333,B333,B333,B333,B333,B333],dim =0)
print("B333 shape is",B333.shape)#(7,5,4,2)
广播后4Dimension multiplied by4维
B4333 =torch.matmul(B4,B333)
print("B4333 shape is",B4333.shape)#(7,5,3,2)
边栏推荐
猜你喜欢
![58: Chapter 5: Develop admin management services: 11: Develop [admin face login, interface]; (not measured) (using Ali AI face recognition) (demonstrated, using RestTemplate to implement interface cal](/img/ab/1c0adeb344329e28010b6ffda5389d.png)
58: Chapter 5: Develop admin management services: 11: Develop [admin face login, interface]; (not measured) (using Ali AI face recognition) (demonstrated, using RestTemplate to implement interface cal

用户体验好的Button,在手机上不应该有Hover态
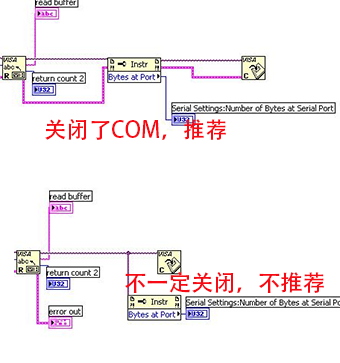
LabVIEW 使用VISA Close真的关闭COM口了吗

Pytorch模型训练实用教程学习笔记:三、损失函数汇总
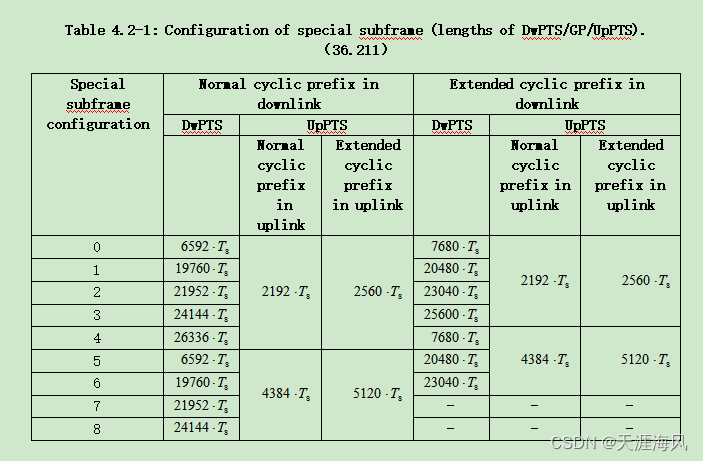
LTE时域、频域资源

使用微信公众号给指定微信用户发送信息
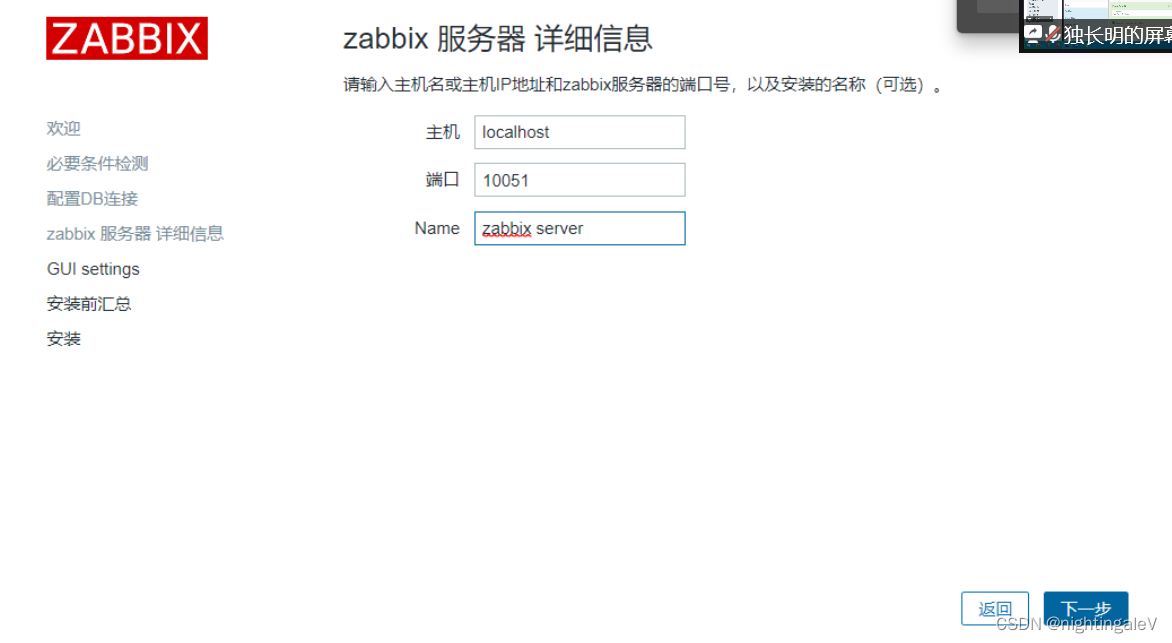
部署zabbix

30-day question brushing plan (5)

八百客、销售易、纷享销客各行其道

Mobile Zero of Likou Brush Questions
随机推荐
突破边界,华为存储的破壁之旅
Ruijie switch basic configuration
【nn.Parameter()】生成和为什么要初始化
MongoDB快速上手
SIPp 安装及使用
Risc-v Process Attack
数据库系统原理与应用教程(070)—— MySQL 练习题:操作题 101-109(十四):查询条件练习
模板特例化和常用用法
【多任务模型】Progressive Layered Extraction: A Novel Multi-Task Learning Model for Personalized(RecSys‘20)
Determine a binary tree given inorder traversal and another traversal method
环境变量,进程地址空间
第58章 结构、纪录与类
【Redis】缓存雪崩、缓存穿透、缓存预热、缓存更新、缓存击穿、缓存降级
LTE时域、频域资源
Win10, the middle mouse button cannot zoom in and out in proe/creo
WhatsApp group sending actual combat sharing - WhatsApp Business API account
洛谷 P2440 木材加工
网络不通?服务丢包?这篇 TCP 连接状态详解及故障排查,收好了~
mysql解压版简洁式本地配置方式
多线程之生产者与消费者