当前位置:网站首页>"Wei Lai Cup" 2022 Niuke summer multi school training camp 2, sign in question GJK
"Wei Lai Cup" 2022 Niuke summer multi school training camp 2, sign in question GJK
2022-07-29 02:11:00 【Little Harry】
Question no title Passed code Passing rate The status of the team
A Falfa with Polygon Click to see 56/445
B light Click to see 50/326
C Link with Nim Game Click to see 192/1035
D Link with Game Glitch Click to see 831/6211
E Falfa with Substring Click to see 264/3287
F NIO with String Game Click to see 52/412
G Link with Monotonic Subsequence Click to see 1667/7564
H Take the Elevator Click to see 290/769
I let fat tension Click to see 204/454
J Link with Arithmetic Progression Click to see 1407/7990
K Link with Bracket Sequence I Click to see 996/3057
L Link with Level Editor I Click to see 564/2616
List of articles
G.Link with Monotonic Subsequence
The question :
- official

Ideas :
- I began to think about the structure (1, 2, 3, 4)(9, 8, 7, ,6 , 5) This arrangement , such The front group forms at most one of the following groups LIS, The answer is n/2+1, Then think about it Get more groups , Can become smaller .
- The structure is like (3, 2, 1),( 6, 5, 4),( 9, 8, 7) Permutation , In this way, each group and the latter group can only choose one , And then if More groups , The length will also increase , On this basis, we should Make each group of elements relatively more , So it is to continue to find the root of the average n, namely Each radical n Elements that will do .
- Pay attention to Rounding up , Because, for example 7 When , Be situated between 2~3 Between , We must choose 3 To reduce the number of groups .
#include<bits/stdc++.h>
using namespace std;
int main(){
int T; cin>>T;
while(T--){
int n; cin>>n;
int sq = ceil(sqrt(n));
for(int i = n; i > 0; i -= sq){
//(7 8 9 )(4 5 6) (1 2 3)
for(int j = max(1,i-sq+1); j <= i; j++)
cout<<j<<" ";
}
cout<<"\n";
}
return 0;
}
J.Link with Arithmetic Progression
The question :
- official :

Ideas :
official :

Let's talk about linear regression
Least square method , That is to minimize the sum of squares of residuals , Is the value required by this question , The square of the difference between the arithmetic sequence and the current sequence .
The proof process can refer to :https://zhuanlan.zhihu.com/p/73494604,
The formula can refer to :https://blog.csdn.net/snowdroptulip/article/details/79020590
#include<bits/stdc++.h>
using namespace std;
typedef long long LL;
typedef long double LD;
const int maxn = 1e6+10;
int a[maxn];
int main(){
int T; cin>>T;
while(T--){
LD n; cin>>n;
LD x = 0, y = 0; // coordinate (i,a[i])
for(int i = 1; i <= n; i++){
cin>>a[i];
x += i; y += a[i];
}
x /= n; y /= n; // expect E(x),E(y), namely x,y mean value
LD s1 = 0, s2 = 0;
for(int i = 1; i <= n; i++){
s1 += (i-x)*(a[i]-y); // covariance :Cov(X,Y) = E[(X-E[X])(Y-E[Y])]?
s2 += (i-x)*(i-x); // variance :D(x) = E[(X-E[X])(X-E[X])]
}
LD k = s1/s2, b = y-k*x; // The formula
LD ans = 0;
for(int i = 1; i <= n; i++){
ans += (a[i]-k*i-b)*(a[i]-k*i-b);
}
printf("%.15Lf\n",ans);
}
return 0;
}
- Three point approach
It is known that f(x) stay l,r Single peak and continuous , Find the extreme value . Each iteration reduces the length of the current interval 1/3 Until we find the extreme value .
We know that the arithmetic sequence is a straight line , This line and all given points (i,a[i]) Finding the smallest variance is the point to find .
So let's set a straight line y = kx+b , namely b^2=(y-kx)^2, Make y=a[i], x=i, At this point, we just need to minimize b The variance of .
b About k Single peak and continuous ,b=f(k).
#include<bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(0), cin.tie(0),cout.tie(0)
typedef long long LL;
typedef long double LD;
const LL maxn = 1e6+10;
const LD eps = 1e-10;
LD a[maxn], b[maxn], n;
LD check(LD k){
//b=y-kx The variance of
LD sum = 0, res = 0;
for(int i = 1; i <= n; i++){
b[i] = a[i]-k*i;
sum += b[i];
}
sum /= n;
for(int i = 1; i <= n; i++){
res += (b[i]-sum)*(b[i]-sum);
}
return res;
}
int main(){
IOS;
int T; cin>>T;
while(T--){
cin>>n;
LD sum = 0;
for(int i = 1; i <= n; i++){
cin>>a[i]; sum += a[i];
}
LD l = -1e15, r = 1e15, ans = 1e100;
while(r-l > eps){
LD mt = (r-l)/3;
LD m1 = l+mt, m2 = r-mt;
LD v1 = check(m1), v2 = check(m2);
if(v1 >= v2){
ans = min(ans, v2);
l = m1;
}else{
ans = min(ans, v1);
r = m2;
}
}
printf("%.15Lf\n",ans);
}
return 0;
}
K.Link with Bracket Sequence I
The question :
- official :

Ideas :
- official

#include<bits/stdc++.h>
using namespace std;
#define IOS ios::sync_with_stdio(0), cin.tie(0),cout.tie(0)
typedef long long LL;
const int maxn = 210;
const int mod = 1e9+7;
LL f[maxn][maxn][maxn];//b front i position ,'(' Than ')' many j individual ,a front k The number of schemes of bit
int main(){
IOS;
int T; cin>>T;
while(T--){
int n, m; cin>>n>>m;
string a; cin>>a;
a = "0"+a;
// memset(f,0,sizeof(f)); //TLE 70%
for (int i = 0; i <= m; ++ i) {
for (int j = 0; j <= m; ++ j) {
for (int k = 0; k <= m; ++ k) {
f[i][j][k] = 0;
}
}
}
f[0][0][0] = 1;
for(int i = 0; i < m; i++){
for(int j = 0; j <= i; j++){
for(int k = 0; k <= i; k++){
// about b[i+1], a[k+1] Choose or not
if(a[k+1]==')'){
if(j>0)(f[i+1][j-1][k+1] += f[i][j][k]) %= mod;
(f[i+1][j+1][k] += f[i][j][k]) %= mod;
}else if(a[k+1]=='('){
(f[i+1][j+1][k+1] += f[i][j][k]) %= mod;
if(j>0)(f[i+1][j-1][k] += f[i][j][k]) %= mod;
}else {
(f[i+1][j+1][k] += f[i][j][k]) %= mod;
if(j>0)(f[i+1][j-1][k] += f[i][j][k]) %= mod;
}
}
}
}
cout<<f[m][0][n]<<"\n";
}
return 0;
}
边栏推荐
- Force deduction brush question (1): sum of two numbers
- 使用本地缓存+全局缓存实现小型系统用户权限管理
- JetPack--Navigation实现页面跳转
- MySQL high performance optimization notes (including 578 pages of notes PDF document), collected
- h5背景音乐通过触摸自动播放
- Leetcode 242. valid anagram
- Mysql存储json格式数据
- 12. < tag dynamic programming and subsequence, subarray> lt.72. edit distance
- Mathematical modeling -- bus scheduling optimization
- [public class preview]: application exploration of Kwai gpu/fpga/asic heterogeneous platform
猜你喜欢

The basic concept of transaction and the implementation principle of MySQL transaction

druid. The performance of IO + tranquility real-time tasks is summarized with the help of 2020 double 11

Flexible layout single selection

基于C51控制蜂鸣器
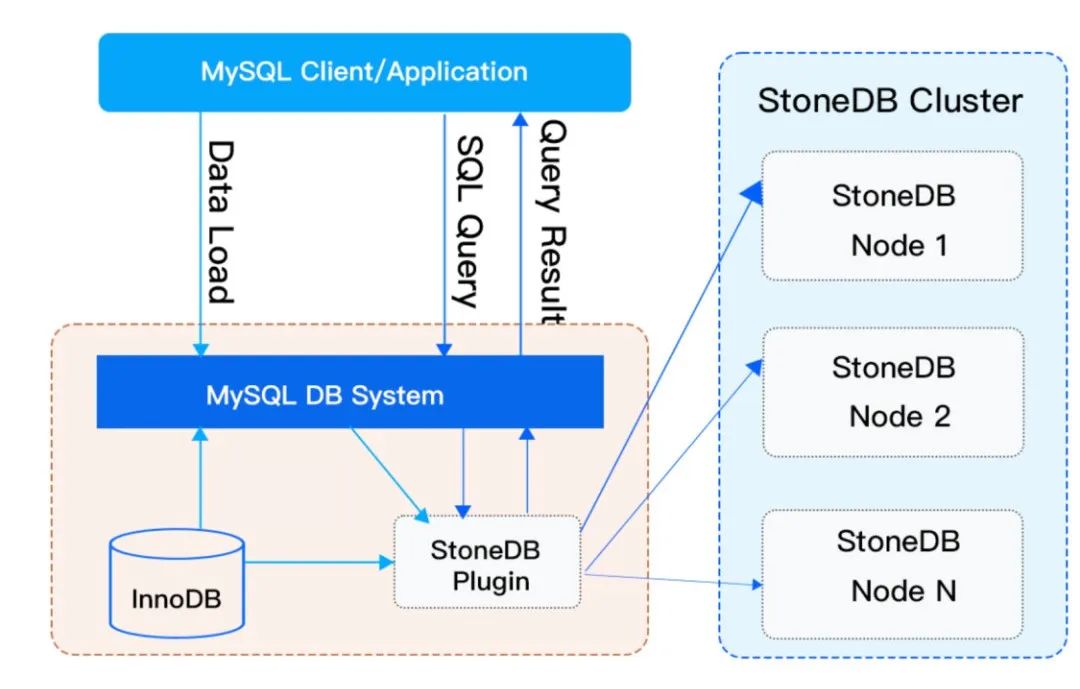
Why does stonedb dare to call it the only open source MySQL native HTAP database in the industry?

Talk about possible problems when using transactions (@transactional)

ciscn 2022 华中赛区 misc
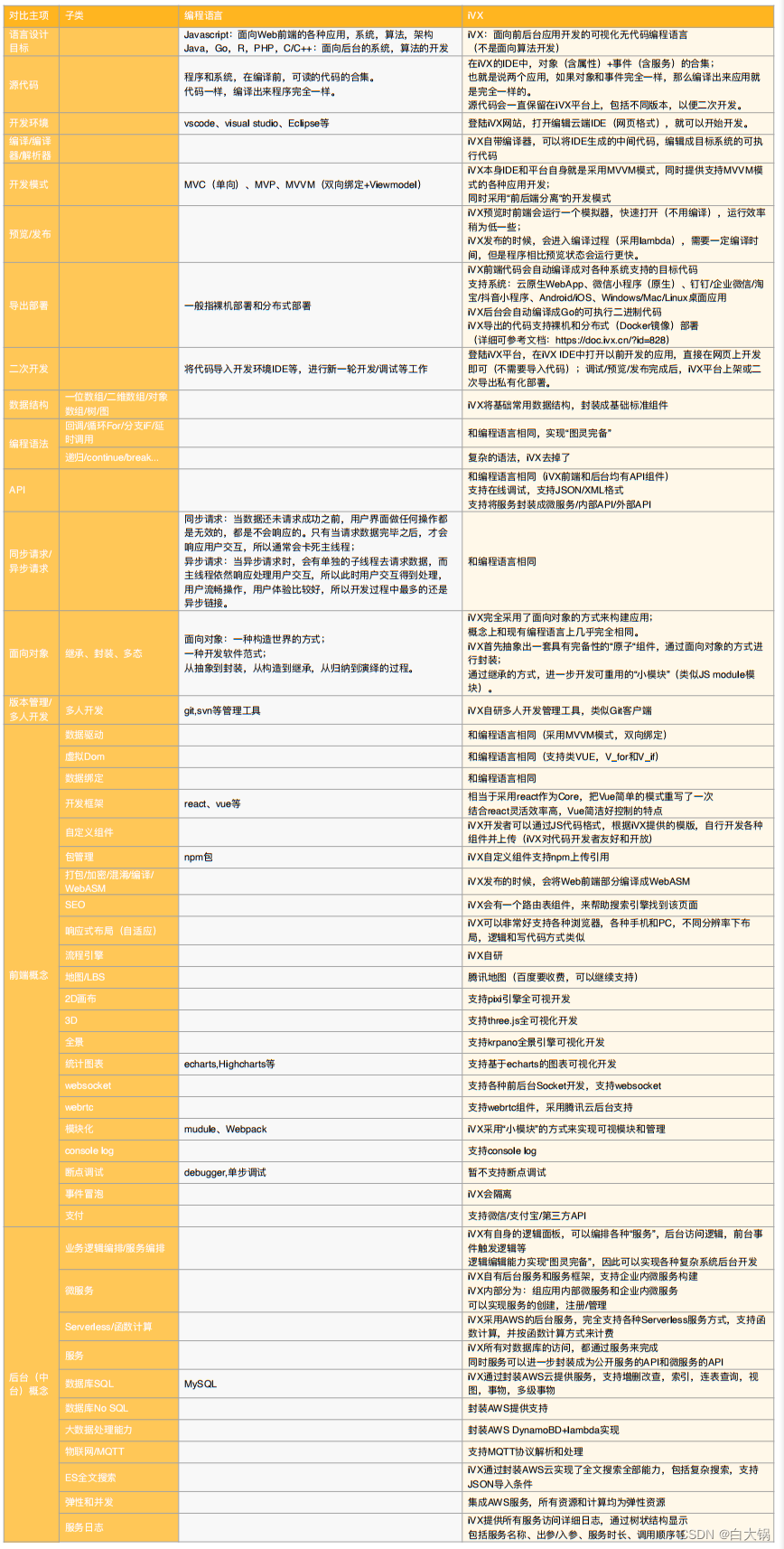
iVX低代码平台系列详解 -- 概述篇(二)

Verilog procedure assignment statements: blocking & non blocking

“蔚来杯“2022牛客暑期多校训练营2,签到题GJK
随机推荐
12.< tag-动态规划和子序列, 子数组>lt.72. 编辑距离
In 2022, the official data of programming language ranking came, which was an eye opener
[circuit design] peak voltage and surge current
Lxml web page capture the most complete strategy
Mathematical modeling -- the laying of water pipes
Flexible layout single selection
Leetcode/ and continuous shortest subarray greater than or equal to target
QT memory management tips
Ciscn 2022 central China Misc
Use POI to export excel file, image URL to export file, image and excel file to export compressed package
Add graceful annotations to latex formula; "Data science" interview questions collection of RI Gai; College Students' computer self-study guide; Personal firewall; Cutting edge materials / papers | sh
基于 ICA 与 DL 的语音信号盲分离
Nine days later, we are together to focus on the new development of audio and video and mystery technology
What is browser fingerprint recognition
Try to understand the essence of low code platform design from another angle
Ignore wechat font settings
druid. The performance of IO + tranquility real-time tasks is summarized with the help of 2020 double 11
MySQL安装常见报错处理大全
Monadic linear function perceptron: Rosenblatt perceptron
数学建模——自来水管道铺设问题