当前位置:网站首页>学习笔记:机器学习之回归
学习笔记:机器学习之回归
2022-08-01 23:51:00 【萌龙如我们】
活动地址:CSDN21天学习挑战赛
1 简介
生活中有很多简单的回归问题,比如某两个变量之间存在显著的线性关系,我们可以用回归来量化分析问题,预测变量。
比如本例子中,我们探究车速和刹车位移之间的关系。
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
cars=pd.read_csv("../data/cars.csv",usecols=["speed","dist"])
cars[:5]#speed为车速,dist为刹车距离,| 0 | 4 | 2 |
| 1 | 4 | 10 |
| 2 | 7 | 4 |
| 3 | 7 | 22 |
| 4 | 8 | 16 |
查看数据的情况
x=cars["speed"]
y=cars["dist"]
plt.title("fig1.Scatter plot of vehicle speed and braking distance")
plt.scatter(x,y,marker="*",c='red')
从图像中我们可以看出两个变量大致存在某种线性关系,接下来我们通过建立回归模型去量化它。
2 回归模型
我们的目的是求出下列函数的参数

其中x为车速,y为刹车距离。
我们需要建立一个函数去衡量预测值和真实值之间的差距大小,这样才能知道我们最后获得的参数的效果如何。
损失函数为:

n为样本数量, 为某次刹车的真实值,
为某次刹车的真实值, 为预测值。
为预测值。
自然地,我们需要L达到最小值,这样获得的回归模型才是最精确的,以下有两种方式。
3 两种求解方式
3.1 直接法
使用直接法可以直接求出最优解,但是需要满足损失函数为凸函数,解为解析解。
【函数的凹凸性】
设一个函数为f(x),图像上有两点
,弦AB上一点为
。
则弦AB的方程为:
其中
,则
.弦AB的参数方程为:
因为f(x)上任A,B所在弦上一点P的函数值大于再f(x)上的函数值,则有:
参数的计算方法参考博客:最小二乘法
实验部分:
import sympy
#设方程为y=ax+b
#回归系数:比例系数a和偏置值b
a,b=sympy.symbols("a b")
L=0.5*np.sum((y-a*x-b)**2)
#求偏导
f1=sympy.diff(L,b)
f2=sympy.diff(L,a)
print(sympy.diff(L,a))
print(sympy.diff(L,b))
ans=sympy.solve([f1,f2],[b,a])
# 所解得{b: -17.5790948905109, a: 3.93240875912409}
alpha=ans[a]
beta=ans[b]
pre=alpha*x+beta
plt.title("Fig2 Fitting results")
plt.scatter(x,y,c="red")
plt.plot(x,pre,c="green")
plt.show()绘制所得到的直线:

则函数关系为:

3.2 迭代法
直接对损失函数进行优化师有局限性的,若损失函数为非凸函数的话很难求出最优解。故此提出迭代法,与之前学习的神经网络的后向传播算法类似,通过不断小幅度更新参数来实现损失值最小化。所以,迭代法与直接法不同之处在于参数的更新方式:前者可以通过直接计算得到,而后者需要经过小批量梯度下降的方式去更新。
此时损失函数为:

 为批量大小
为批量大小
目标求解:
参数更新: 为学习率
为学习率
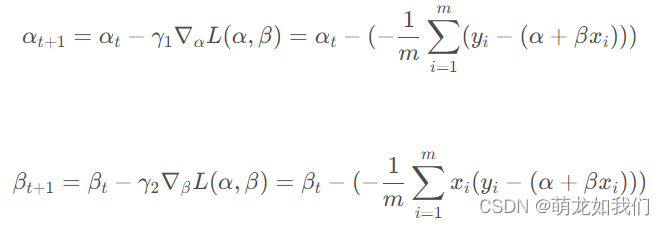
实验部分:
import random
#变量更新函数
def update_var(pre_alpha,pre_beta,y,x,lr):
n=len(x)
diff_alpha=np.sum(-(y-pre_beta*x-pre_alpha))/n
diff_beta =np.sum(-x*(y-pre_beta*x-pre_alpha))/n
new_alpha=pre_alpha-lr*diff_alpha
new_beta=pre_beta-lr*diff_beta
return (new_alpha,new_beta)
#实现迭代过程
def iterative_func(y,x,raw_alpha,raw_beta,lr,num,sample_num):
alpha_list = []
beta_list = []
alpha = raw_alpha
beta = raw_beta
num_list = list(range(1, len(y)+1))
for i in range(num):
alpha_list.append(alpha)
beta_list.append(beta)
random.shuffle(num_list)
index = num_list[:sample_num]
alpha, beta = update_var(alpha, beta,y[index], x[index], lr)
print("【{}】Now alpha:{},beta:{}".format(i,alpha,beta))
return (alpha_list, beta_list)
#随机初始化alpha和beta
raw_alpha=np.random.random()*10
raw_beta =np.random.random()*10
raw_alpha
#设置超参数:学习率lr=0.005 迭代次数num=2000,sample_num=16
lr = 0.005
num = 10000
sample_num = 16
alpha_list, beta_list = iterative_func(y, x, raw_alpha, raw_beta,
lr, num,sample_num)
print("after {} times iteration:alpha: {}, beta:{}".format(num,alpha_list[-1], beta_list[-1]))after 10000 times iteration:alpha: -17.791370073935074, beta:4.000650060840287
#将参数迭代过程产生的数据持久化
import csv
var_data=zip(alpha_list,beta_list)
with open("../data/20220801_vardata.csv",'w',newline='')as f:
csv_writer=csv.writer(f)
csv_writer.writerows(['alpha','beta'])
csv_writer.writerows(var_data)
plt.subplot(121)
plt.plot(alpha_list)
plt.title("alpha change process")
plt.subplot(122)
plt.plot(beta_list)
plt.title("beta change process")
plt.show()
参考
边栏推荐
- windows sql server 如何卸载干净?
- 高效工作文档产出归类
- Building a cloud-native DevOps environment
- 【Leetcode】475. Heaters
- Wincc报表教程(SQL数据库的建立,wincc在数据库中保存和查询数据,调用Excel模板把数据保存到指定的位置和打印功能)
- cdh6 opens oozieWeb page, Oozie web console is disabled.
- 6133. Maximum number of packets
- 12306抢票,极限并发带来的思考?
- asyncawait和promise的区别
- Convert LocalDateTime to Date type
猜你喜欢
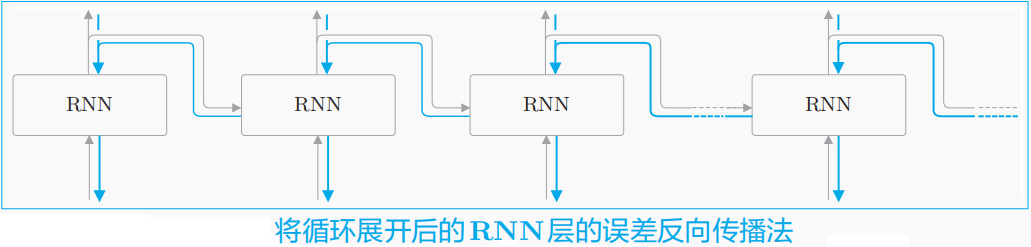
深度学习基础-基于Numpy的循环神经网络(RNN)实现和反向传播训练
UI自动化测试框架搭建-标记性能较差用例
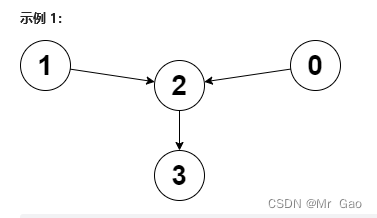
6134. Find the closest node to the given two nodes - force double hundred code

windows sql server 如何卸载干净?
Excel导入和导出

带你搞懂MySQL隔离级别,两个事务同时操作同一行数据会怎样?
Quartus uses tcl files to quickly configure pins
12306抢票,极限并发带来的思考?
The third chapter of the imitation cattle network project: develop the core functions of the community (detailed steps and ideas)
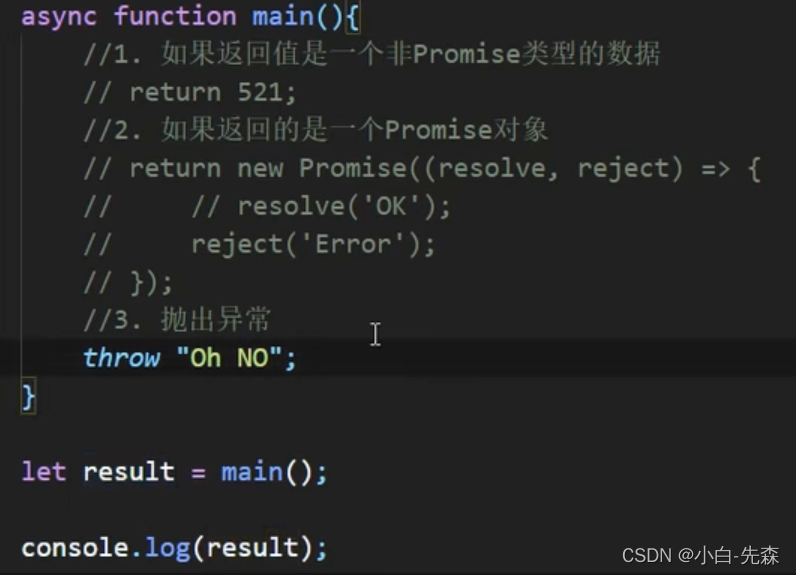
async和await用法介绍
随机推荐
JAX-based activation function, softmax function and cross entropy function
Classical Literature Reading--DLO
Flink学习第五天——Flink可视化控制台依赖配置和界面介绍
如何用Redis实现分布式锁?
字节跳动面试官:请你实现一个大文件上传和断点续传
Getting started with IDEA is enough to read this article
【MySQL系列】MySQL索引事务
【Leetcode】479. Largest Palindrome Product
thinkphp漏洞总结
技术分享 | 接口测试中如何使用Json 来进行数据交互 ?
在MySQL中使用MD5加密【入门体验】
The Spark of Sql join on the and and where
sys_kill system call
Avoid hidden text when loading fonts
正则表达式
@Transactional 注解使用详解
yay 报错 response decoding failed: invalid character ‘<‘ looking for beginning of value;
numpy.isclose
2022还想上岸学习软件测试必看,测试老鸟的肺腑之言...
Win10安装DBeaver连接MySQL8、导入和导出数据库详细教程
 ,弦AB上一点为
,弦AB上一点为 。
。
 ,则
,则 .弦AB的参数方程为:
.弦AB的参数方程为:
