当前位置:网站首页>Methods of finding various limits
Methods of finding various limits
2022-07-01 19:28:00 【Debroon】
The method of finding various limits
Direct substitution
- lim x − > 3 ( x + 1 ) \lim\limits_{x->3}(x+1) x−>3lim(x+1)
x The limit of is close to 3, Is in the 3 near , Let's go straight to x=3 Plug in x+1 Middle computation , have to 4.
There are some exceptions :
- often Count ∞ = 0 \frac{ constant }{∞}=0 ∞ often Count =0
- ∞ often Count = ∞ \frac{∞}{ constant }=∞ often Count ∞=∞
- Not zero often Count 0 = ∞ \frac{ Nonzero constant }{0}=∞ 0 Not zero often Count =∞
- ∞ > 0 = ∞ ∞^{>0}=∞ ∞>0=∞
- ∞ < 0 = 1 ∞ > 0 = 0 ∞^{<0}=\frac{1}{∞^{>0}}=0 ∞<0=∞>01=0
- n ∞ = 0 , 0 > n > 1 n^{∞}=0,0>n>1 n∞=0,0>n>1
- n ∞ = ∞ , n > 1 n^{∞}=∞,n>1 n∞=∞,n>1
∞ ∞ \frac{∞}{∞} ∞∞ type
Some problems cannot be solved directly , such as ∞ ∞ \frac{∞}{∞} ∞∞ type , It's not a specific number , It's a trend .
- lim x − > ∞ x 100 + x − 1001 + x x 1000 + 2 x \lim\limits_{x->∞}\frac{x^{100}+x^{-1001}+x}{x^{1000}+2x} x−>∞limx1000+2xx100+x−1001+x
solution : Grasp the main trends
In many trends (∞) in , We need to find the biggest trend , Because that is the most influential item .
∞ ∞ \frac{∞}{∞} ∞∞ type , Solving steps :
- Identify trends
- Look at the index , molecular 、 The denominator retains the largest trend
lim x − > ∞ x 100 + x − 1001 + x x 1000 + 2 x \lim\limits_{x->∞}\frac{x^{100}+x^{-1001}+x}{x^{1000}+2x} x−>∞limx1000+2xx100+x−1001+x
- = lim x − > ∞ ∞ 100 + ∞ − 1001 + ∞ ∞ 1000 + 2 ∞ \lim\limits_{x->∞}\frac{∞^{100}+∞^{-1001}+∞}{∞^{1000}+2∞} x−>∞lim∞1000+2∞∞100+∞−1001+∞
- = lim x − > ∞ ∞ + 0 + ∞ ∞ + ∞ \lim\limits_{x->∞}\frac{∞+0+∞}{∞+∞} x−>∞lim∞+∞∞+0+∞
- = lim x − > ∞ x 100 x 1000 \lim\limits_{x->∞}\frac{x^{100}}{x^{1000}} x−>∞limx1000x100
- = lim x − > ∞ 1 x 900 \lim\limits_{x->∞}\frac{1}{x^{900}} x−>∞limx9001
- = lim x − > ∞ 1 ∞ 900 \lim\limits_{x->∞}\frac{1}{∞^{900}} x−>∞lim∞9001
- = 1 ∞ \frac{1}{∞} ∞1
- = 0 0 0
solution : Use lobita's law
0 0 \frac{0}{0} 00 type
lim x − > 0 x s i n x = 0 0 \lim\limits_{x->0}\frac{x}{sinx}=\frac{0}{0} x−>0limsinxx=00
When put x − > 0 x->0 x−>0 After substituting into the formula , Will become 0 0 \frac{0}{0} 00, There will also be no solution .
solution : Replace with equivalent infinitesimal
When a part tends to 0 when , There are five situations :
Case one , x − > 0 , s i n x = x x->0,sin x = x x−>0,sinx=x,
- lim x − > 0 x s i n x = x x = 1 \lim\limits_{x->0}\frac{x}{sinx}=\frac{x}{x}=1 x−>0limsinxx=xx=1
The second case , 1 − c o s Δ 1-cos\Delta 1−cosΔ Variable to 1 2 Δ 2 \frac{1}{2}\Delta^{2} 21Δ2
- lim x − > 0 1 − c o s x x = lim x − > 0 1 2 x 2 x \lim\limits_{x->0}\frac{1-cosx}{x}=\lim\limits_{x->0}\frac{\frac{1}{2}x^{2}}{x} x−>0limx1−cosx=x−>0limx21x2
The nature of the following three cases is the same , Are all forms of substitution .
solution : Use lobita's law
If the unknown x − > 0 、 x − > ∞ x->0、x->∞ x−>0、x−>∞ After substitution , The formula is 0 0 \frac{0}{0} 00 or ∞ ∞ \frac{∞}{∞} ∞∞ , be lim f ( x ) g ( x ) = lim f ′ ( x ) g ′ ( x ) \lim\limits \frac{f(x)}{g(x)}=\lim\limits \frac{f'(x)}{g'(x)} limg(x)f(x)=limg′(x)f′(x), Molecules become derivatives of molecules 、 The denominator becomes the derivative of the denominator .
∞ ⋅ 0 ∞·0 ∞⋅0 type
lim x − > ∞ x ( c o s 1 x − 1 ) \lim\limits_{x->∞}x(cos\frac{1}{x}-1) x−>∞limx(cosx1−1)
- = ∞ · (cos 0 - 1)
- = ∞ · 0
Direct substitution encounters ∞ ⋅ 0 ∞·0 ∞⋅0, There is no result .
We have another solution :
- Find the simplest one a
- Turn this item into 1 1 a \frac{1}{\frac{1}{a}} a11
lim x − > ∞ x ( c o s 1 x − 1 ) \lim\limits_{x->∞}x(cos\frac{1}{x}-1) x−>∞limx(cosx1−1)
- = lim x − > ∞ 1 1 x ( c o s 1 x − 1 ) \lim\limits_{x->∞}\frac{1}{\frac{1}{x}}(cos\frac{1}{x}-1) x−>∞limx11(cosx1−1)
- = lim x − > ∞ c o s 1 x − 1 1 x \lim\limits_{x->∞}\frac{cos\frac{1}{x}-1}{\frac{1}{x}} x−>∞limx1cosx1−1
- = 0 0 \frac{0}{0} 00
Index 、 There are all bases x The limits of
Form like : lim x − > 0 ( 1 + 3 x ) 2 s i n x \lim\limits_{x->0}(1+3x)^{\frac{2}{sinx}} x−>0lim(1+3x)sinx2
hold At the end of Count finger Count base number ^{ Index } At the end of Count finger Count become e finger Count ⋅ l n At the end of Count e^{ Index ·ln base number } e finger Count ⋅ln At the end of Count
lim x − > 0 ( 1 + 3 x ) 2 s i n x = lim x − > 0 e 2 s i n x l n ( 1 + 3 x ) \lim\limits_{x->0}(1+3x)^{\frac{2}{sinx}}=\lim\limits_{x->0}e^{\frac{2}{sinx}ln(1+3x)} x−>0lim(1+3x)sinx2=x−>0limesinx2ln(1+3x)
= lim x − > 0 e 2 l n ( 1 + 3 x ) s i n x \lim\limits_{x->0}e^{\frac{2ln(1+3x)}{sinx}} x−>0limesinx2ln(1+3x)
lim x − > ? e finger Count = e lim x − > ? finger Count \lim\limits_{x->?}e^{ Index }=e^{\lim\limits_{x->?} Index } x−>?lime finger Count =ex−>?lim finger Count
= e lim x − > 0 2 l n ( 1 + 3 x ) s i n x e^{\lim\limits_{x->0}}{\frac{2ln(1+3x)}{sinx}} ex−>0limsinx2ln(1+3x)
Left and right limits of function
It is necessary to find the left and right limits
There are three limits , Only through the most primitive method — Find the left and right limits .
- The first category , Functions are segmented functions with braces , The required limit is the limit at the segment point .
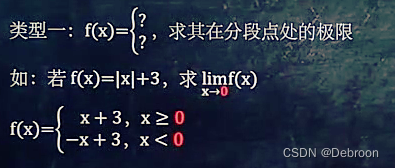
- The second category , Count g ( x ) g^{(x)} g(x) stay g ( x ) g(x) g(x) The denominator of is 0 Limit at .

- The third category , a r c t a n g ( x ) arctan ~g(x) arctan g(x) stay g ( x ) g(x) g(x) The denominator of is 0 Limit at

How to do questions :
- First find the left limit 、 Right limit
- When the left limit = Right limit = Not for ∞ The number of hours , Functional limits exist , And limit = Left limit = Right limit
- When the left limit = Right limit = -∞ perhaps +∞ when , The limit of the function is ∞ / non-existent / There are no limits
- When the left limit != Right limit And Existence is not for ∞ The value of , The function limit does not exist And Not for ∞
边栏推荐
- 混沌工程平台 ChaosBlade-Box 新版重磅发布
- XML syntax, constraints
- B2B e-commerce platform solution for fresh food industry to improve the standardization and transparency of enterprise transaction process
- 宝,运维100+服务器很头疼怎么办?用行云管家!
- 制造业SRM管理系统供应商全方位闭环管理,实现采购寻源与流程高效协同
- 【森城市】GIS数据漫谈(一)
- Lake Shore—CRX-EM-HF 型低温探针台
- CDGA|从事通信行业,那你应该考个数据管理证书
- Lake Shore—OptiMag 超导磁体系统 — OM 系列
- kubernetes命令入门(namespaces,pods)
猜你喜欢

Junit单元测试框架详解

水产行业智能供应链管理平台解决方案:支撑企业供应链数字化,提升企业管理效益
Specification of lumiprobe reactive dye indocyanine green
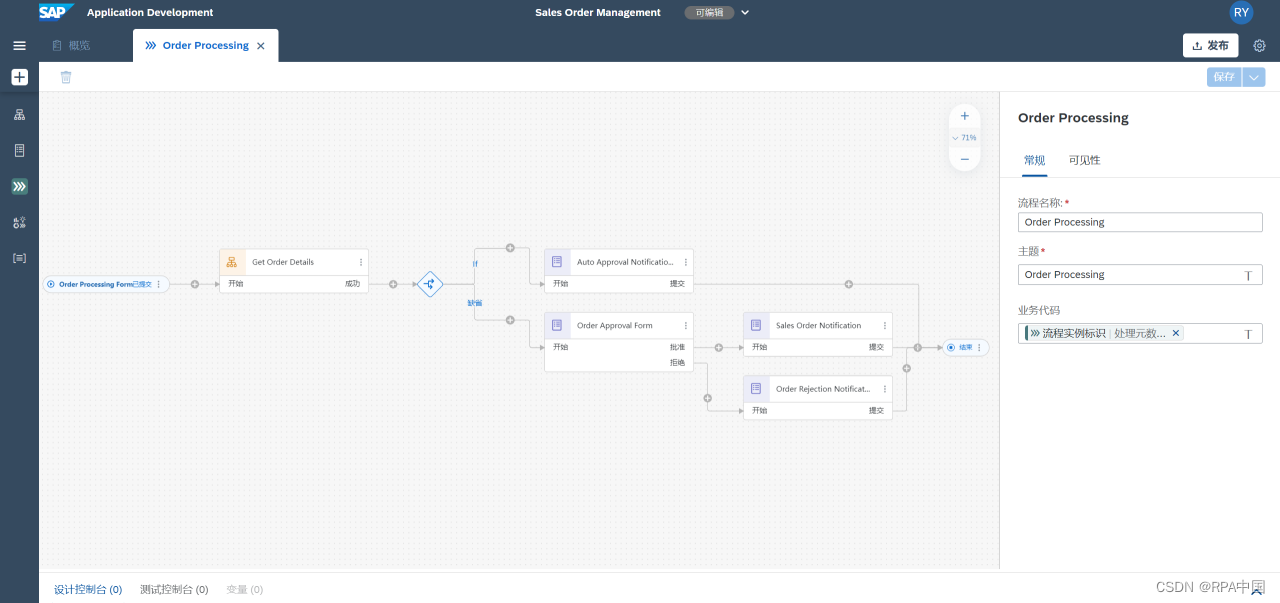
赋能「新型中国企业」,SAP Process Automation 落地中国

Love business in Little Red Book
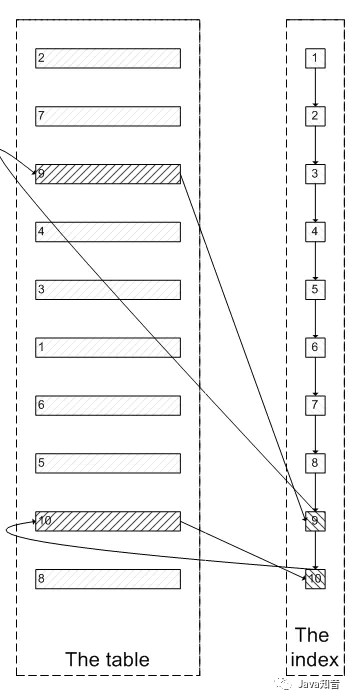
一次SQL优化,数据库查询速度提升 60 倍
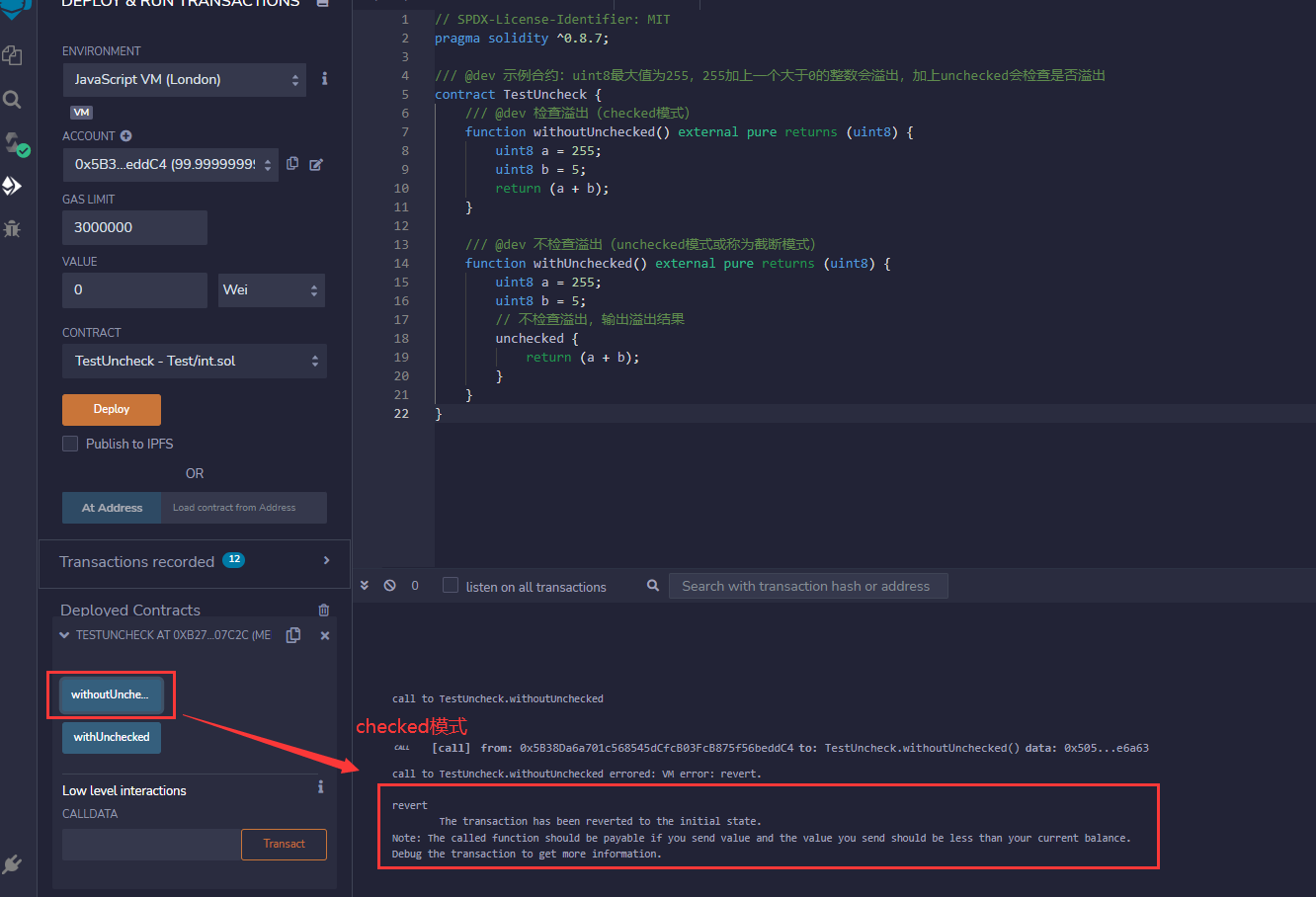
Solidity - 算术运算的截断模式(unchecked)与检查模式(checked)- 0.8.0新特性
Lumiprobe cell imaging study PKH26 cell membrane labeling kit
![[quick application] there are many words in the text component. How to solve the problem that the div style next to it will be stretched](/img/5c/b0030fd5fbc07eb94013f2699c2a04.png)
[quick application] there are many words in the text component. How to solve the problem that the div style next to it will be stretched
白盒加密技术浅理解
随机推荐
微信公众号开发相关流程及功能介绍
[to.Net] C set class source code analysis
Team up to learn! 14 days of Hongmeng equipment development "learning, practicing and testing" practical camp, free of charge!
Contos 7 搭建sftp之创建用户、用户组以及删除用户
MySQL常用图形管理工具 | 黑马程序员
奔赴山海之前,毕业季一定要做的那些事情
Solidity - 算术运算的截断模式(unchecked)与检查模式(checked)- 0.8.0新特性
【6.24-7.1】写作社区精彩技术博文回顾
Huawei game failed to initialize init with error code 907135000
Boost the development of digital economy and consolidate the base of digital talents - the digital talent competition was successfully held in Kunming
任务:拒绝服务DoS
市值蒸发740亿,这位大佬转身杀入预制菜
Junit单元测试框架详解
Lumiprobe cell imaging study PKH26 cell membrane labeling kit
Reading the paper [learning to discretely compose reasoning module networks for video captioning]
ubuntu14安装MySQL并配置root账户本地与远程访问
Games202 operation 0 - environment building process & solving problems encountered
Learning notes [Gumbel softmax]
[AGC] how to solve the problem that the local display of event analysis data is inconsistent with that in AGC panel?
案例分享:QinQ基本组网配置