将移位距离和假设外推到非二值化问题

(A，B)---m*n*k---(1,0)(0,1)

用神经网络分类A和B，A中只有1个0.8，B中有x和y两个值，让x和y分别等于0.1，0.2，…，0.9.观察随着x和y值的变化迭代次数是如何变化的。

比如其中的一组数据811

0.8	1	1		1	1	1
1	1	1		1	1	1
1	1	1		1	0.1	0.1
		811
f2[0]	f2[1]	迭代次数n	平均准确率p-ave	1-0	0-1	δ	耗时ms/次	耗时ms/199次	耗时 min/199	最大准确率p-max	迭代次数标准差	pave标准差
0.301706	0.698295	29717.14	1	1	1	5.00E-04	102.7487	20474			2190.285	0
0.326772	0.673228	36239.3	1	1	1	4.00E-04	122.8543	24459			2725.067	0
0.306649	0.693351	46756.14	1	1	1	3.00E-04	154.4523	30754			3445.346	0
0.301587	0.698413	67224.02	1	1	1	2.00E-04	238.7286	47522			4595.061	0
0.34174	0.65826	129399	1	1	1	1.00E-04	461.1558	91782			10303.36	0

仅统计当收敛误差等于1e-4时的迭代次数，因此811的迭代次数是129399.用同样的办法计算其他各组，共收敛了5*81*199次，得到表格

	1	2	3	4	5	6	7	8	9
	迭代次数n	迭代次数n	迭代次数n	迭代次数n	迭代次数n	迭代次数n	迭代次数n	迭代次数n	迭代次数n
1	129399	132705.9	136683.7	140018	144374.1	147932.7	150717.1	151902.4	153174.6
2	132705.9	137232.4	142921.4	146234.6	150101.2	154450.4	158519.5	160066.4	163884
3	136683.7	142921.4	148447.7	154052.8	160116.9	163318.7	167953.8	172673.4	177175.9
4	140018	146234.6	154052.8	160888	167867.1	175446.3	182787.5	189270.9	192287.7
5	144374.1	150101.2	160116.9	167867.1	178011.5	188866.1	198233.1	205875.1	214260.2
6	147932.7	154450.4	163318.7	175446.3	188866.1	203627.7	217644	232628.4	243062.8
7	150717.1	158519.5	167953.8	182787.5	198233.1	217644	238568.6	260051.9	277977.9
8	151902.4	160066.4	172673.4	189270.9	205875.1	232628.4	260051.9	299941.8	324286.2
9	153174.6	163884	177175.9	192287.7	214260.2	243062.8	277977.9	324286.2	382095

让x=0.1，y=0.2，或者让y=0.1，x=0.2得到的值是一样的。因此这个表格是对称的。如第一列第二行的132705.9就是812或者821的值。

	1	2	3	4	5	6	7	8	9
	迭代次数n	迭代次数n	迭代次数n	迭代次数n	迭代次数n	迭代次数n	迭代次数n	迭代次数n	迭代次数n
1	129399	132705.9	136683.7	140018	144374.1	147932.7	150717.1	151902.4	153174.6

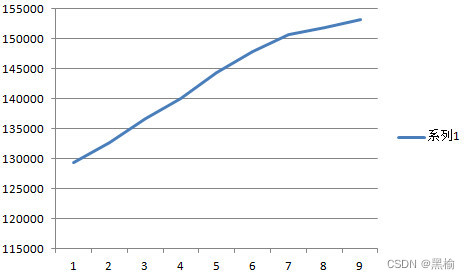
当x=0.1，y逐渐增加迭代次数是增加的。同样当y不变x增加也会导致迭代次数增加。所以如果x和y同时增加，迭代次数是增加的。

	1	2	3	4	5	6	7	8	9
	迭代次数n	迭代次数n	迭代次数n	迭代次数n	迭代次数n	迭代次数n	迭代次数n	迭代次数n	迭代次数n
1	129399	132705.9	136683.7	140018	144374.1	147932.7	150717.1	151902.4	153174.6
2	132705.9	137232.4	142921.4	146234.6	150101.2	154450.4	158519.5	160066.4	163884
3	136683.7	142921.4	148447.7	154052.8	160116.9	163318.7	167953.8	172673.4	177175.9
4	140018	146234.6	154052.8	160888	167867.1	175446.3	182787.5	189270.9	192287.7
5	144374.1	150101.2	160116.9	167867.1	178011.5	188866.1	198233.1	205875.1	214260.2
6	147932.7	154450.4	163318.7	175446.3	188866.1	203627.7	217644	232628.4	243062.8
7	150717.1	158519.5	167953.8	182787.5	198233.1	217644	238568.6	260051.9	277977.9
8	151902.4	160066.4	172673.4	189270.9	205875.1	232628.4	260051.9	299941.8	324286.2
9	153174.6	163884	177175.9	192287.7	214260.2	243062.8	277977.9	324286.2	382095

如对角线，显然是899>888>,…,>811.所以如果x和y都等于1则81010>899.所以1为底的情况下，将B二值化将得到8xy迭代次数的极大值。这可以用移位距离和假设去解释，因为如果把B中的点全变成1，则B的复杂度降低，熵减小迭代次数增加。

或者考虑一个极端情况，把A中的数值也二值化，则A和B将都只有1，二者是相同的，迭代次数无限大。因此对于以1为底的图片，二值化可以得到图片迭代次数的极大值。

另外按照移位距离和假设的外推，对于非二值化图片，单次移位的距离或许就是移位元素的数值，

	1	2	3	4	5	6	7	8	9
	迭代次数n	迭代次数n	迭代次数n	迭代次数n	迭代次数n	迭代次数n	迭代次数n	迭代次数n	迭代次数n
1	129399	132705.9	136683.7	140018	144374.1	147932.7	150717.1	151902.4	153174.6
2	132705.9	137232.4	142921.4	146234.6	150101.2	154450.4	158519.5	160066.4	163884
3	136683.7	142921.4	148447.7	154052.8	160116.9	163318.7	167953.8	172673.4	177175.9
4	140018	146234.6	154052.8	160888	167867.1	175446.3	182787.5	189270.9	192287.7
5	144374.1	150101.2	160116.9	167867.1	178011.5	188866.1	198233.1	205875.1	214260.2
6	147932.7	154450.4	163318.7	175446.3	188866.1	203627.7	217644	232628.4	243062.8
7	150717.1	158519.5	167953.8	182787.5	198233.1	217644	238568.6	260051.9	277977.9
8	151902.4	160066.4	172673.4	189270.9	205875.1	232628.4	260051.9	299941.8	324286.2
9	153174.6	163884	177175.9	192287.7	214260.2	243062.8	277977.9	324286.2	382095

比较

844	853	862	871
160887.95	160116.91	154450.43	150717.08

0.4+0.4=0.5+0.3=0.6+0.2=0.7+0.1，所以844，853，862，871按照移位距离和假设的外推他们的移位距离应该是相同的都是0.8，所以他们的迭代次数也应该是相同的。

以1为底的图片，数值增加将使得迭代次数增加，因此从844到853，由4变为5使得迭代次数增加了，而由4变为3却使得迭代次数变小了，

	3	4	5
	迭代次数n	迭代次数n	迭代次数n
1	136683.693	140017.98	144374.12		3334.2915	4356.1307
2	142921.437	146234.64	150101.24		3313.201	3866.598
3	148447.683	154052.76	160116.91		5605.0754	6064.1558
4	154052.759	160887.95	167867.07		6835.196	6979.1106
5	160116.915	167867.07	178011.48		7750.1508	10144.417
6	163318.719	175446.33	188866.08		12127.608	13419.754
7	167953.809	182787.5	198233.13		14833.688	15445.633
8	172673.392	189270.95	205875.1		16597.558	16604.146
9	177175.879	192287.69	214260.24		15111.809	21972.548

比较8x3,8x4,8x5的迭代次数，用8x5-8x4，再用8x4-8x3，可以发现把4变成5的迭代次数增量，大于把4变成3的迭代次数减量。因此由于这种不均匀的变化导致844，853，862，871的迭代次数彼此之间出入较大。

可以合理的猜测如果数值的变化对迭代次数的影响是一条直线，则移位距离和假设外推到非二值化问题将是严格成立的。

所以移位距离和假设对非二值化问题，并不严格正确，但也仅仅是有误差，

876	885	894
217643.98	205875.1	192287.69

比如比较876，885，894。0.7+0.6=0.8+0.5=0.9+0.4=1.3，这3组的值要接近的多。对于以1为底的图片如果定义移位距离为1-元素数值，则876的移位距离为2-1.3=0.7而844的移位距离2-0.8=1.2.因此1.2>0.7按照移位距离和迭代次数的反比关系，876，885，894的迭代次数要大于844，853，862，871，这与观测是一致的。

所以有理由把移位距离和假设外推到非二值化问题

(A，B)---m*n*k---(1,0)(0,1)

移位距离和假设

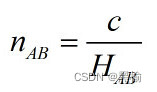
用神经网络分类A和B，把参与分类的A和B中的数字看作是组成A和B的粒子，分类的过程就是让A和B中的粒子互相交换位置，寻找最短移位路径的过程。而熵H与最短移位距离和成正比，迭代次数n和熵H成反比。

移位规则汇总

每个粒子移位一次，位置重合不移位，0不动，单次移位距离如果以1为底等于1-元素数值若以0为底则为元素本身。