当前位置:网站首页>AcWing 234 放弃测试
AcWing 234 放弃测试
2022-06-29 12:17:00 【昂昂累世士】
题目描述
在某个课程中,你需要进行 n 次测试。
如果你在共计 bi 道题的测试 i 上的答对题目数量为 ai,你的累积平均成绩就被定义为

给定您的考试成绩和一个正整数 k,如果您被允许放弃任何 k 门考试成绩,您的累积平均成绩的可能最大值是多少。
假设您进行了 3 次测试,成绩分别为 5/5,0/1 和 2/6。
在不放弃任何测试成绩的情况下,您的累积平均成绩是
。
然而,如果你放弃第三门成绩,则您的累积平均成绩就变成了
。
输入格式
输入包含多组测试用例,每个测试用例包含三行。
对于每组测试用例,第一行包含两个整数 n 和 k。
第二行包含 n 个整数,表示所有的 ai。
第三行包含 n 个整数,表示所有的 bi。
当输入用例 n=k=0 时,表示输入终止,且该用例无需处理。
输出格式
对于每个测试用例,输出一行结果,表示在放弃 k 门成绩的情况下,可能的累积平均成绩最大值。
结果应四舍五入到最接近的整数。
数据范围
1≤n≤1000,
0≤k<n,
0≤ai≤bi≤109
输入样例:
3 1
5 0 2
5 1 6
4 2
1 2 7 9
5 6 7 9
0 0
输出样例:
83
100
分析
本题属于01分数规划的模板题。01分数规划是这样的一类问题,有一堆物品,每一个物品有一个收益ai,一个代价bi,我们要求一个方案使选择的∑ai / ∑bi 最大。比如说在n个物品中选k个物品,使得∑ai / ∑bi 最大。
01分数规划的问题看起来挺复杂,其实就是求两个数组的部分和之商的最值。我们不知道最值是多少,比如本题,a和b中都有n个数字,我们要放弃k个数字,也就是在n个元素中选择n - k个元素,对其a和b数组选中的元素求和。暴力做法就是枚举放弃的k道题目,一共C(n,k)种方案,全部枚举出来求最值,显然复杂度很高。
另一种方法就是二分答案,二分法需要问题具有单调性,如果我们二分到一个解t,只要能够判断是否存在一个方案使得∑ai / ∑bi >= t即可,如果存在这样的方案,那么最大解一定不会在t的左边。而在求合法方案时,不便之处在于表达式∑ai / ∑bi 是分数形式,不妨对∑ai / ∑bi >= t变形下得到∑ai - t * ∑bi >= 0,这样左边的表达式就可以写成一个新的数组了,令c[i] = a[i] - t * b[i],原问题就转化为了是否存在合法方案使得c的部分和不小于0了,我们对c数组排下序,选择其中最大的n - k个元素,求出的和必然是选n - k个元素能够求出的最大的,只要这个和不小于0,证明存在不小于k的解。
总结下01分数规划问题的二分解法,就是二分解,并且将分数形式的表达式转化为非分数形式的表达式,将比较难求方案的表达式变形成好求方案的表达式。
代码
#include <iostream>
#include <cstdio>
#include <algorithm>
const int N = 1005;
using namespace std;
int n,k;
double a[N],b[N],c[N];
bool check(double t){
for(int i = 0;i < n;i++) c[i] = a[i] - t * b[i];
sort(c,c + n);
double s = 0;
for(int i = n - 1;i >= k;i--) s += c[i];
if(s >= 0) return true;
return false;
}
int main(){
while(cin>>n>>k,n){
for(int i = 0;i < n;i++) cin>>a[i];
for(int i = 0;i < n;i++) cin>>b[i];
double l = 0,r = 1e9;
while(r - l > 1e-6){
double mid = (l + r) / 2;
if(check(mid)) l = mid;
else r = mid;
}
int res = 100 * l + 0.5;
printf("%d\n",res);
}
return 0;
}
边栏推荐
- File contained log poisoning (user agent)
- C # clue binary tree through middle order traversal
- Definition of C # clue binary tree
- C#通過中序遍曆對二叉樹進行線索化
- SCHIEDERWERK电源维修SMPS12/50 PFC3800解析
- NvtBack
- Interview shock 61: tell me about MySQL transaction isolation level?
- Newton inequality
- Proteus Software beginner notes
- Beifu PLC controls servo through CANopen communication
猜你喜欢

Comparison table of LR and Cr button batteries
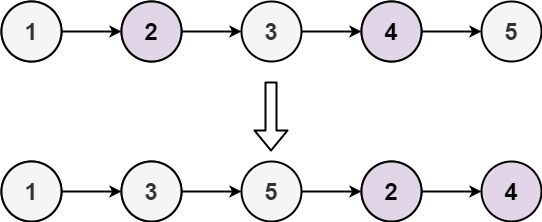
LeetCode_双指针_中等_328.奇偶链表
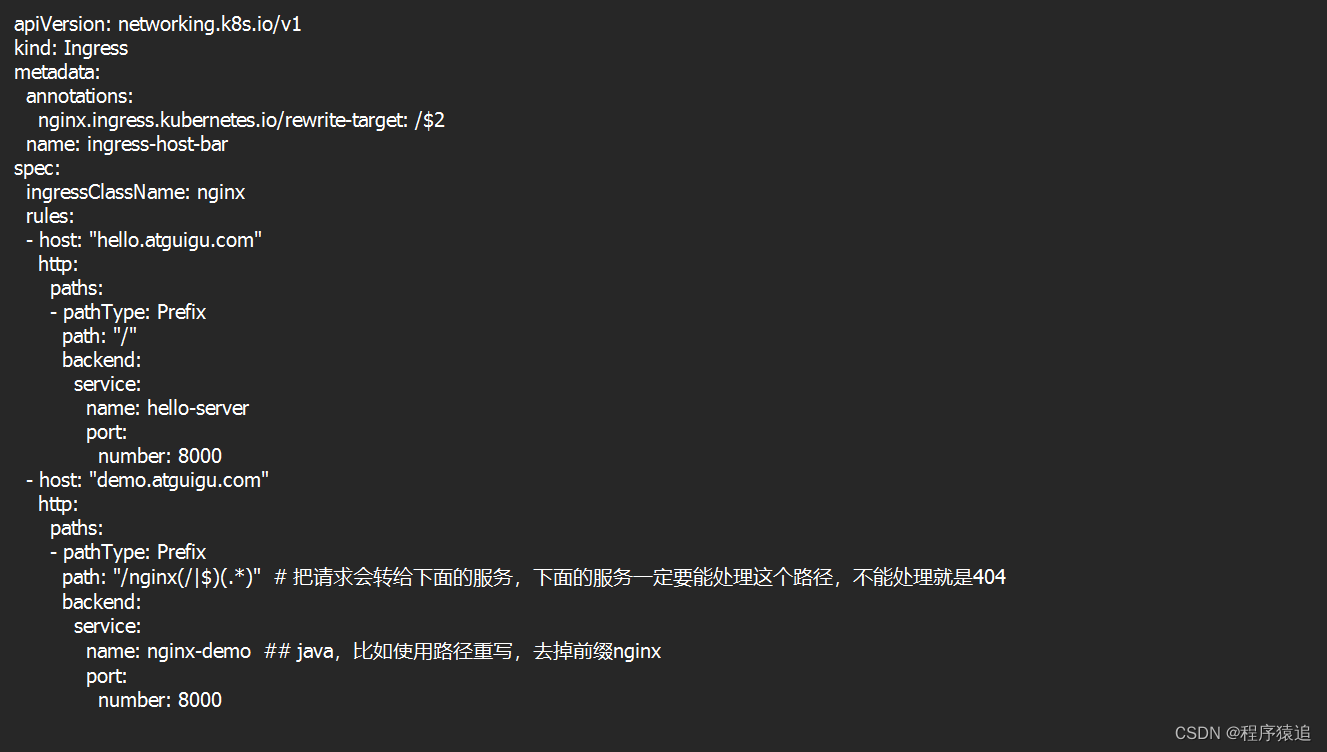
【云原生】2.4 Kubernetes 核心实战(中)

缓存一致性,删除缓存,写入缓存,缓存击穿,缓存穿透,缓存雪崩

LR、CR纽扣电池对照表

Definition of C # clue binary tree
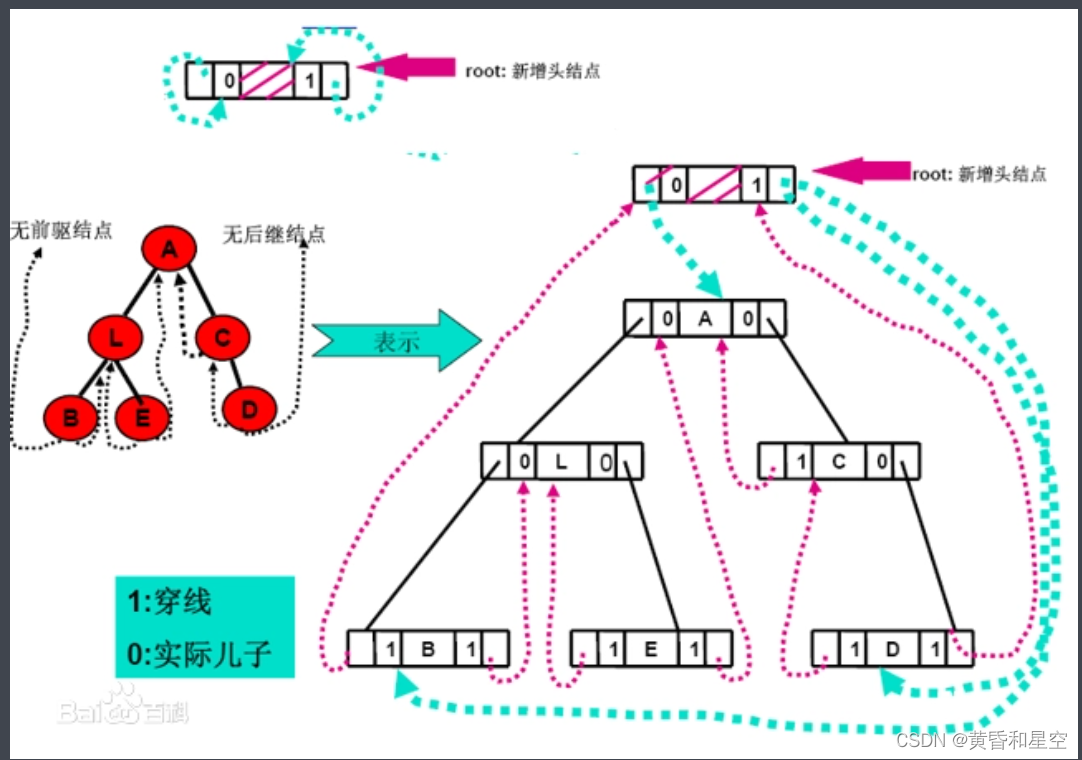
C # clue binary tree through middle order traversal

Earth observation satellite data
![[cloud native] 2.4 kubernetes core practice (middle)](/img/1e/b1b22caa03d499387e1a47a5f86f25.png)
[cloud native] 2.4 kubernetes core practice (middle)
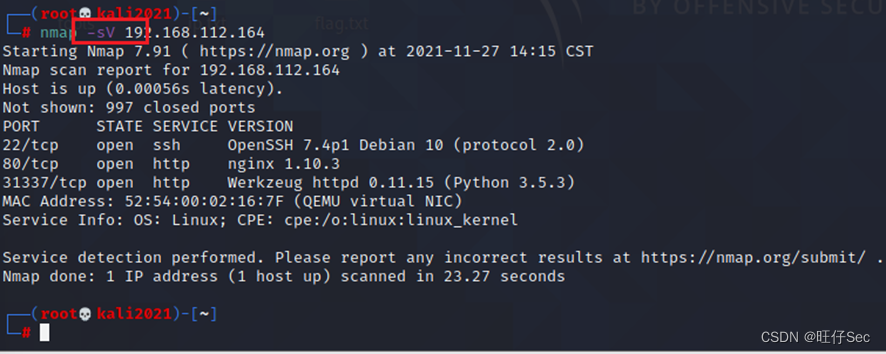
Application Service Vulnerability scanning and exploitation of network security skills competition in secondary vocational schools (SSH private key disclosure)
随机推荐
MIT linear algebra Chinese Notes
C # indexe l'arbre binaire en traversant l'ordre moyen
Detailed explanation on configuration and commissioning of third-party servo of Beifu TwinCAT -- Taking Huichuan is620n as an example
如何计算win/tai/loss in paired t-test
Inferiority complex and transcendence the meaning of life to you
Interview shock 61: tell me about MySQL transaction isolation level?
How to calculate win/tai/loss in paired t-test
Kyligence Zen, an intelligent indicator driven management and decision-making platform, is newly launched and is in limited internal testing
ZALSM_ EXCEL_ TO_ INTERNAL_ Solving the big problem of importing data from table
Newton inequality
C # implementation of binary tree non recursive middle order traversal program
推荐模型复现(四):多任务模型ESMM、MMOE
墨菲安全入选中关村科学城24个重点项目签约
Baidu cloud disk downloads large files without speed limit (valid for 2021-11 personal test)
Recurrence of recommended models (IV): multi task models esmm and MMOE
535. encryption and decryption of tinyurl: design a URL simplification system
C # realizes the first order traversal, middle order traversal and second order traversal of binary tree
测试--自动化测试:关于unittest框架
23、 1-bit data storage (delay line / core /dram/sram/ tape / disk / optical disc /flash SSD)
Nacos startup error