当前位置:网站首页>小红的aba子序列(离散化、二分、dp维护区间最短)
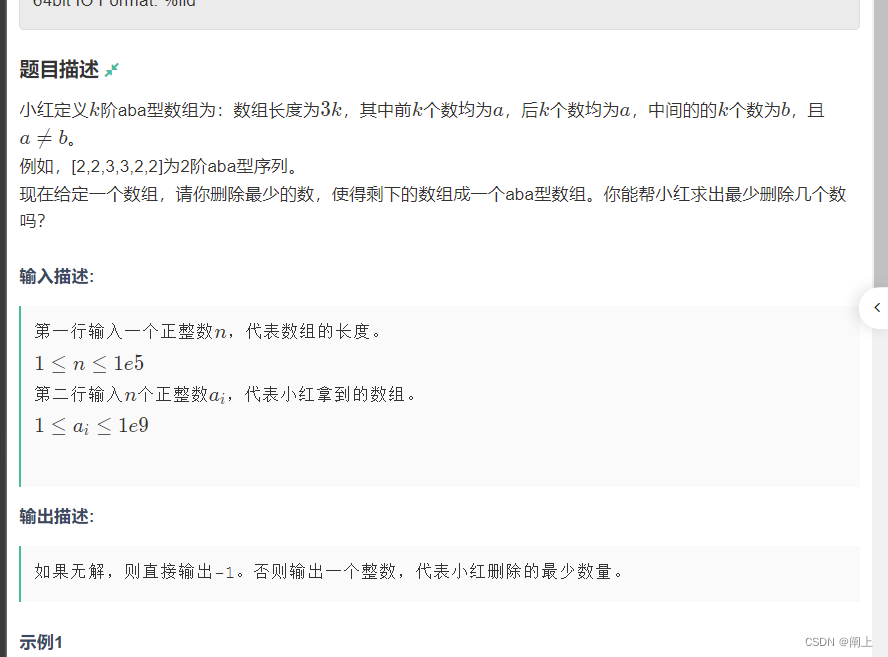
小红的aba子序列(离散化、二分、dp维护区间最短)
2022-08-05 11:15:00 【阐上】
TP
思路:
- 显然每种数离散化一下,记录下对应出现的坐标。
- 枚举每一种数,排除前 k 个和后 k 个后,中间的区间就是需要查找的是否有可能满足情况。
- 直接维护是很困难的,这题用了二分的方法,二分 k 的值,对于每种 k check 一下每种数上面说的那个区间是否有解。
C o d e : Code: Code:
#include<bits/stdc++.h>
#include<unordered_map>
#define debug cout << "debug--- "
#define debug_ cout << "\n---debug---\n"
#define oper(a) operator<(const a& ee)const
#define forr(a,b,c) for(int a=b;a<=c;a++)
#define mem(a,b) memset(a,b,sizeof a)
#define cinios (ios::sync_with_stdio(false),cin.tie(0),cout.tie(0))
#define all(a) a.begin(),a.end()
#define sz(a) (int)a.size()
#define endl "\n"
#define ul (u << 1)
#define ur (u << 1 | 1)
using namespace std;
typedef unsigned long long ull;
typedef long long ll;
typedef pair<ll, int> PII;
const int N = 1e5 + 10, M = 2e6 + 10, mod = 1e9 + 7;
int INF = 0x3f3f3f3f; ll LNF = 0x3f3f3f3f3f3f3f3f;
int n, m, B = 10, ki;
int a[N];
vector<int> vec[N];
int f1[N], f2[N], id[N];
//f[i] 意为第 i 位最早的 j,满足 区间 [i,j] 有 k 个值相同的数
//预处理最小、次小的 f1[i],f2[i],满足最小、次小的 k 个值相同的数 值不同
//
//id[i] 记录 f1[i] 的 k 个值相同的数 值是多少
bool check(int mid) {
for (int i = 1; i <= n; i++)f1[i] = f2[i] = id[i] = INF;
//对于每一种数,找到长度为 mid 的区间维护
for (int i = 1; i <= m; i++) {
int siz = vec[i].size();
for (int j = mid - 1; j < siz; j++) {
int be = vec[i][j - mid + 1];
int ed = vec[i][j];
f1[be] = ed, id[be] = i;
//因为某位只能存在一种数,所以只有f1
/* if (f1[be] > ed) { f2[be] = f1[be], f1[be] = ed; id[be] = i; } else if (f2[be] > ed)f2[be] = ed;*/
}
}
//反向 dp,每一位维护右边最早能形成 k 个数的 位置
for (int i = n - 1; i >= 1; i--) {
//能更新最小,则次小获得最小,更新最小
if (f1[i] > f1[i + 1]) {
if (id[i] != id[i + 1])f2[i] = f1[i];
f1[i] = f1[i + 1], id[i] = id[i + 1];
}
//否则,当且仅当数类型不同才更新最小
else if (f2[i] > f1[i + 1] && id[i] != id[i + 1])f2[i] = f1[i + 1];
if (f2[i] > f2[i + 1])f2[i] = f2[i + 1];
//次小随意更新
}
for (int i = 1; i <= m; i++) {
int siz = sz(vec[i]);
//最后对于每种数,找到累计 k 个的最左端和最右端
if (siz >= mid + mid) {
int l = vec[i][mid - 1], r = vec[i][siz - mid];
//判断是否有 中间的的 k 个数为 b,且a ≠ b
if (f1[l] < r && id[l] != i || f2[l] < r)return true;
}
}
return false;
}
void solve() {
cin >> n;
m = 0;
map<int, int> mp;//离散化
forr(i, 1, n) {
cin >> a[i];
if (!mp.count(a[i]))mp[a[i]] = ++m;
a[i] = mp[a[i]];
vec[a[i]].push_back(i);
}
int l = 1, r = n / 3;
while (l < r)
{
int mid = l + r + 1 >> 1;
if (check(mid))l = mid;
else r = mid - 1;
}
//最后一定还要check一下,有可能无解
if (!check(l))cout << -1;
else cout << n - l * 3;
}
int main() {
cinios;
int T = 1;
for (int t = 1; t <= T; t++) {
solve();
}
return 0;
}
/* */
边栏推荐
猜你喜欢

《分布式云最佳实践》分论坛,8 月 11 日深圳见
再获殊荣 | 赛宁网安入选2022年度“培育独角兽”企业榜单
365 days challenge LeetCode1000 questions - Day 050 add a row to the binary tree binary tree
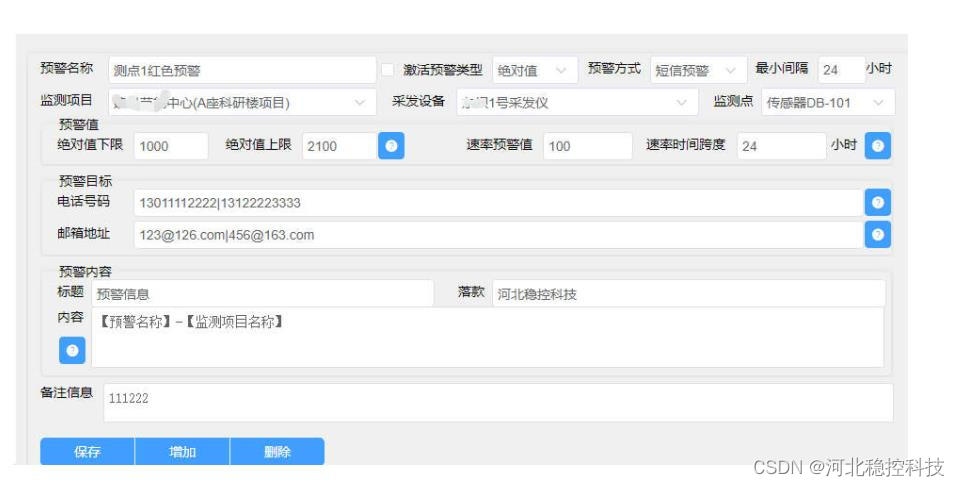
工程设备在线监测管理系统自动预警功能

MySQL 中 auto_increment 自动插入主键值

【MySQL基础】-【数据处理之增删改】
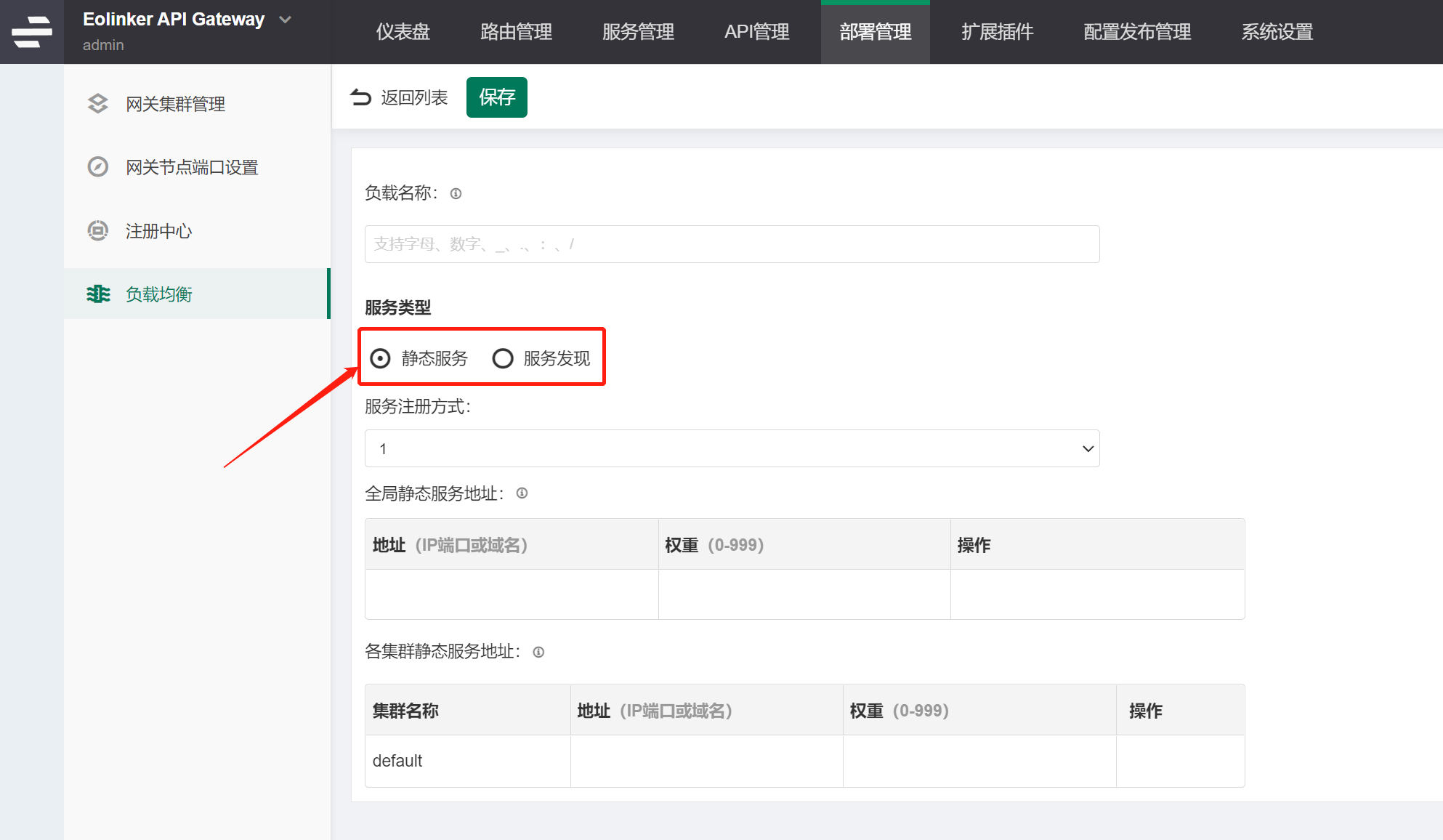
API 网关简述

硅谷来信:快速行动,Facebook、Quora等成功的“神器”!
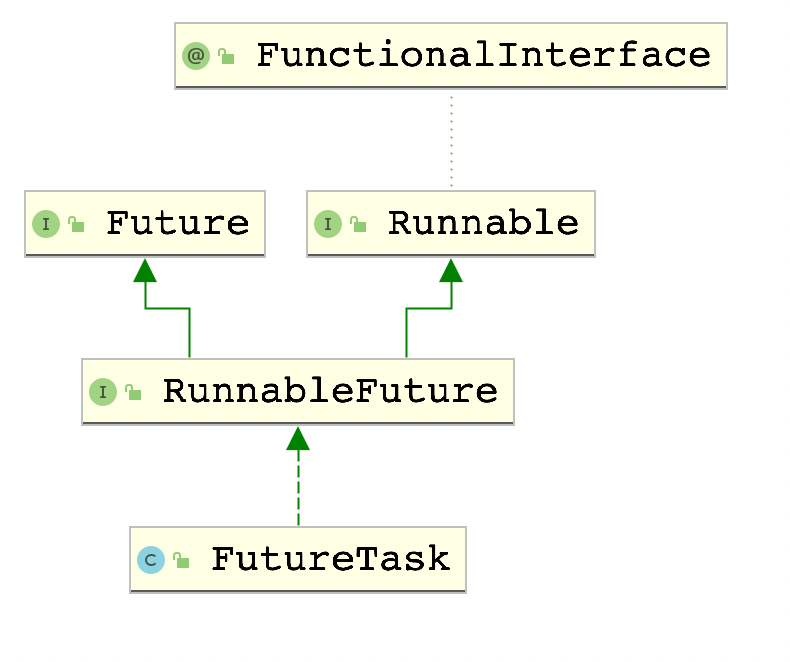
60行从零开始自己动手写FutureTask是什么体验?
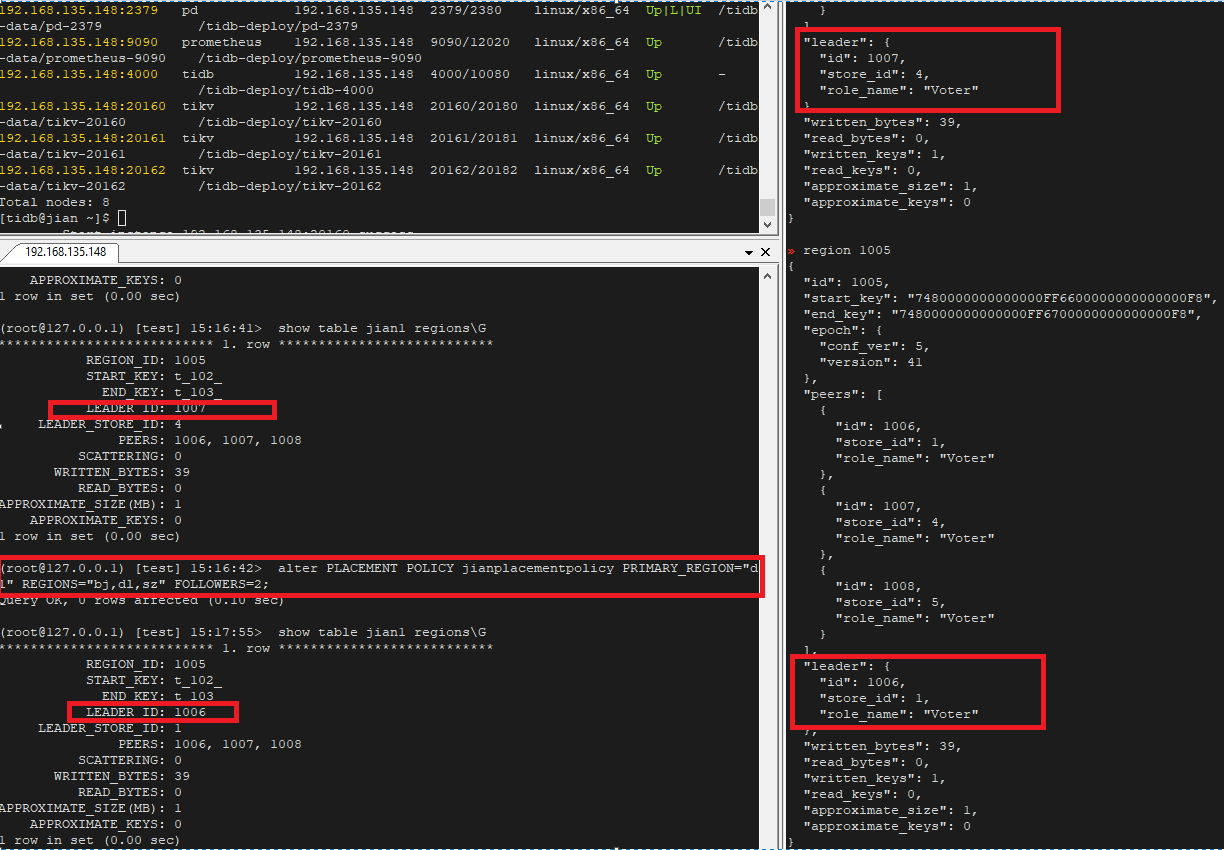
TiDB 6.0 Placement Rules In SQL 使用实践
随机推荐
拓朴排序例题
I'm going crazy.Again A few days can not be A problem
GPU-CUDA-图形渲染分析
《分布式云最佳实践》分论坛,8 月 11 日深圳见
Three methods for extracting facial features
UDP通信
hdu4545 魔法串
SMB + SMB2: Accessing shares return an error after prolonged idle period
SkiaSharp 之 WPF 自绘 投篮小游戏(案例版)
lvgl 实现状态提示图标自动对齐补位显示
我要抓狂了。。又回到了几天不能A一道题的时候
2022技能大赛训练题:交换机snmp配置
什么是 DevOps?看这一篇就够了!
Latex如何控制表格的宽度和高度
【名词】什么是PV和UV?
微信小程序标题栏封装
Android development with Kotlin programming language - basic data types
nyoj757 期末考试 (优先队列)
提取人脸特征的三种方法
A small test of basic grammar, Go lang1.18 introductory refining tutorial, from Bai Ding to Hongru, basic grammar of go lang and the use of variables EP02