详解浮点数的精度问题

前言

相信大家在学习编程语言的变量类型的浮点数的时候，都有听说过“浮点数的精度是有限的”，即0.1+0.2不等于0.3，那么究竟是为什么呢？

其实这个问题非常简单，只要我们转换一下视角就可以了。我们之所以知道 0.1+0.2=0.3，是因为我们使用的是十进制，而计算机判断他们不相等，根本原因是因为计算机使用的是二进制。

十进制小数转化成二进制

首先我们要知道我们使用的十进制，在二进制的计算机世界中是怎么样的。已经知道如何转换的同学可以直接跳过这部分。

十进制的整数部分和小数部分转化成二进制的方法是不一样的，十进制整数转二进制使用的是「除 2 取余法」，十进制小数使用的是「乘 2 取整法」。

十进制 8.625 转化为二进制就是 1000.101，即 2^3 + 2^-1 + 2^-3 = 8+0.5+0.125。

其实二进制小数并不能表示所有的小数，只能表达2 除尽的数字，比如 1/2=0.1，1/4=0.01，3/4=0.11，1/8=0.001；而像0.1，0.2，0.3这种小数，就不能用二进制完整表示（就像十进制无法精确表示1/3，1/7一样），所以使用二进制的计算机碰上这种小数，只能尽其所能表示，也就出现了精度问题。

计算机是怎么存小数的-浮点数

1000.101 这种表达是「定点数」形式，代表着小数点是固定的，不能移动，如果你移动了它的小数点，这个数就被改变了。

然而，计算机并不是这样存储的小数的，计算机存储小数的采用的是浮点数，表示小数点是可以浮动的。

比如 1000.101 这个二进制数，可以表示成 1.000101 x 2^3，类似于数学上的科学记数法。

浮点数表达规定，要保证基数为 2，并且小数点左侧只有 1 位，且必须为 1。（即一定要表示为 1.xxx * 2^x，0.11 要表示成 1.1 * 2^-1）

所以需要将 1000.101 这种二进制数，规格化表示为 1.000101 x 2^3，其中，最为关键的是指数和尾数，可以包含了这个二进制小数的所有信息：

• 000101 称为尾数，即小数点后面的数字；
• 3 称为指数，指定了小数点在数据中的位置；

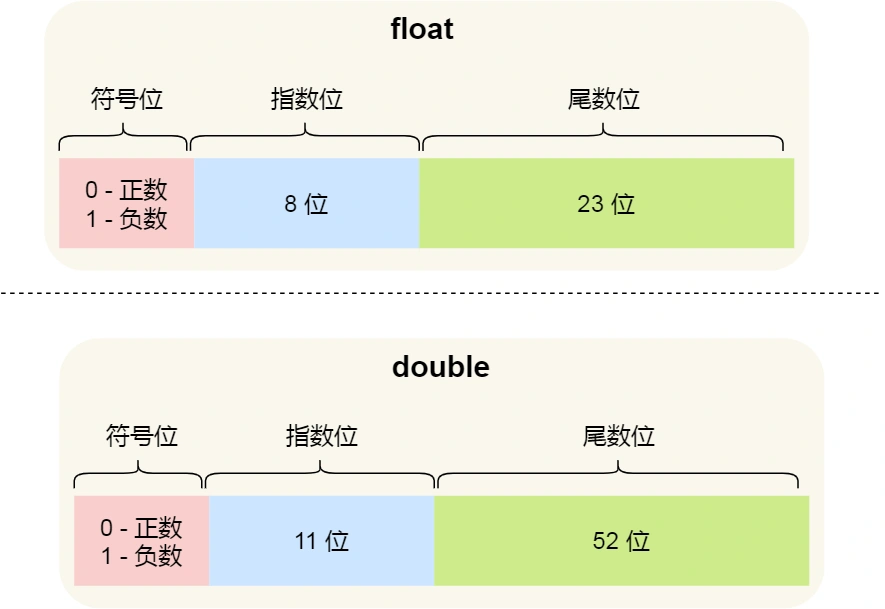
现在绝大多数计算机使用的浮点数，一般采用的是 IEEE 制定的国际标准，这种标准形式如下图：

这三个重要部分的意义如下：

• 符号位：表示数字是正数还是负数，为 0 表示正数，为 1 表示负数；
• 指数位：指定了小数点在数据中的位置，指数可以是负数，也可以是正数，指数位的长度越长则数值的表达范围就越大；
• 尾数位：小数点右侧的数字，也就是小数部分，尾数的长度决定了这个数的精度，因此如果要表示精度更高的小数，则就要提高尾数位的长度；

用 32 位来表示的浮点数，则称为单精度浮点数，也就是编程语言中的 float 变量，而用 64 位来表示的浮点数，称为双精度浮点数，也就是 double 变量，它们的结构如下：

可以看到：

• float 的尾数部分是 23 位，double 的尾数部分是 52 位，由于同时都带有一个固定隐含位（这个后面会说），所以 float 有 24 个二进制有效位，double 有 53 个二进制有效位，所以它们的精度在十进制中分别是 log10(2^24) 约等于 7.22 位和 log10(2^53) 约等于 15.95 ，因此 float 的有效数字是 7~8 位，double 的有效数字是 15~16 位，这些有效位是包含整数部分和小数部分；
• float 的指数位是 8 位，double 的指数部分是 11 位，所以它们的范围分别是 2^104-2^128~2^128-2^104，约等于±2^128 和 2^971-2^1024~2^1024-2^971，约等于±2^1024。

那二进制小数，是如何转换成二进制浮点数的呢？

我们就以 10.625 作为例子，看看这个数字在 float 里是如何存储的。

首先，我们计算出 10.625 的二进制小数为 1010.101。

然后把小数点，移动到第一个有效数字后面，即将 1010.101 右移 3 位成 1.010101，右移 3 位就代表 +3，左移 3 位就是 -3。

float 中的「指数位」就跟这里移动的位数有关系，把移动的位数再加上「偏移量」，float 的话偏移量是 127，相加后就是指数位的值了，即指数位这 8 位存的是 10000010（十进制 130），因此你可以认为「指数位」相当于指明了小数点在数据中的位置。

为什么要加偏移量？

指数可能是正数，也可能是负数，即指数是有符号的整数，而有符号整数的计算是比无符号整数麻烦的，所以为了减少不必要的麻烦，在实际存储指数的时候，需要把指数转换成无符号整数。float 的指数部分是 8 位，IEEE 标准规定单精度浮点的指数取值范围是 -126 ~ +127，于是为了把指数转换成无符号整数，就要加个偏移量，比如 float 的指数偏移量是 127，这样指数就不会出现负数了。

比如，指数如果是 8，则实际存储的指数是 8 + 127（偏移量）= 135，即把 135 转换为二进制之后再存储，而当我们需要计算实际的十进制数的时候，再把指数减去「偏移量」即可。

1.010101 这个数的小数点右侧的数字就是 float 里的「尾数位」，由于尾数位是 23 位，则后面要补充 0，所以最终尾数位存储的数字是 01010100000000000000000。

细心的朋友肯定发现，移动后的小数点左侧的有效位（即 1）消失了，它并没有存储到 float 里。

这是因为 IEEE 标准规定，二进制浮点数的小数点左侧只能有 1 位，并且还只能是 1，既然这一位永远都是 1，那就可以不用存起来了。

于是就让 23 位尾数只存储小数部分，然后在计算时会自动把这个 1 加上，这样就可以节约 1 位的空间，尾数就能多存一位小数，相应的精度就更高了一点。

那么，对于我们在从 float 的二进制浮点数转换成十进制时，要考虑到这个隐含的 1，转换公式如下：

举个例子，我们把下图这个 float 的数据转换成十进制，过程如下：

总结

1. 为什么浮点数会有精度问题？

答：因为计算机使用的是二进制，而二进制并不能完整表示所有小数，对于无法完整表示的小数，只能尽量用接近值表示，所以浮点数会存在精确度问题，而且 double 类型比 float 类型更精确。

2. 两个浮点数相加一定与另一个浮点数不相等吗？

答：不一定。如果等号两边都是可以完整表示的小数，那么等式成立。因为等号不成立的根本原因是浮点数无法完整表达部分小数。

• 0.1 + 0.2 == 0.3（false）
• 0.1 + 0.5 == 0.6 （false）
• 0.5 + 0.125 == 0.625（true）

参考

小林coding https://xiaolincoding.com/os/1_hardware/float.html