当前位置：网站首页>LeetCode - 102. 二叉树的层序遍历；110. 平衡二叉树；098. 验证二叉搜索树
LeetCode - 102. 二叉树的层序遍历；110. 平衡二叉树；098. 验证二叉搜索树
2022-08-03 17:36:00 【NPE~】
LeetCode
一、LeetCode - 102. 二叉树的层序遍历
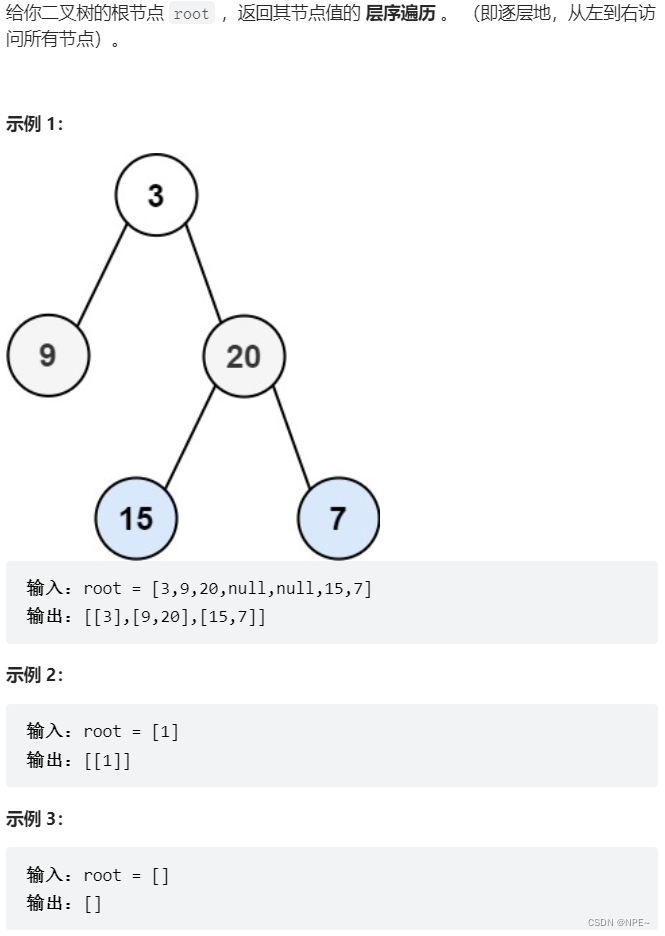
首先，层序遍历表明，是一层一层来存放，并且是从上到下一层一层遍历【我们可以使用队列的结构来存放（类比“遍历文件夹”）】
1 创建queue，根据链表中的size来判断poll的次数
每次记录queue的size，表明队列中还有几个元素，然后挨个弹出node，并且在弹出的过程中，判断node的左子树与右子树是否为null，如果不为null，添加进queue（相当于进行深层次遍历）
int size = queue.size();
ArrayList<Integer> list = new ArrayList<>();
while(size > 0){
TreeNode node = queue.poll();
list.add(node.val);
if(node.left != null){
queue.add(node.left);
}
if(node.right != null){
queue.add(node.right);
}
size--;
}
res.add(list);
2 全代码
class Solution {
private List<List<Integer>> res = new ArrayList<>();
public List<List<Integer>> levelOrder(TreeNode root) {
if(root == null) return res;
LinkedList<TreeNode> queue = new LinkedList<>();
queue.add(root);
while(!queue.isEmpty()){
int size = queue.size();
ArrayList<Integer> list = new ArrayList<>();
while(size > 0){
TreeNode node = queue.poll();
list.add(node.val);
if(node.left != null){
queue.add(node.left);
}
if(node.right != null){
queue.add(node.right);
}
size--;
}
res.add(list);
}
return res;
}
}
拓展：如果该题目没有要求用List的话，可以使用数组来代替（速度会更快）
// while(!queue.isEmpty()){
// int size = queue.size();
// int[] list = new int[size];
// for(int i = 0; i <= size; ++i){
// TreeNode node = queue.poll();
// list[i] = node.val;
// if(node.left != null){
// queue.add(node.left);
// }
// if(node.right != null){
// queue.add(node.right);
// }
// }
// res.add(list);
// }
二、LeetCode - 110. 平衡二叉树
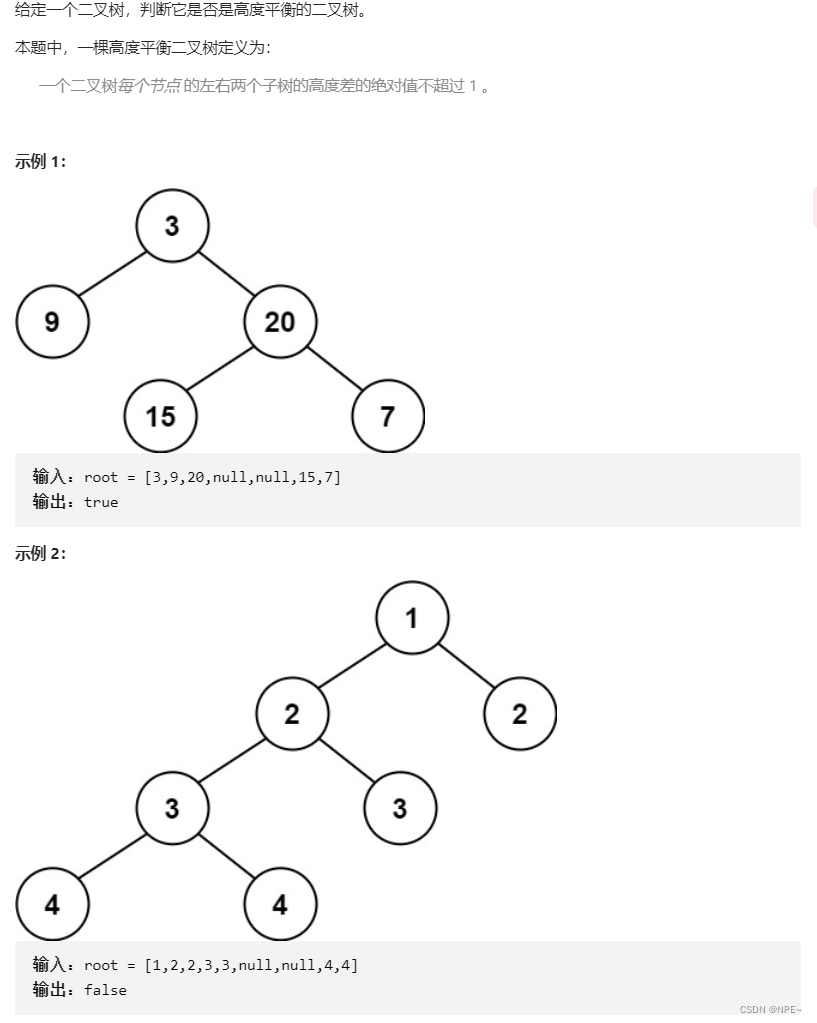
平衡二叉树：叶子节点的高度差不超过1；
因此，我们只需要构造函数，记录以该节点为根节点，判断是否是平衡二叉树，同时，记录下该节点高度，最后判断两叶子节点高度差是否不超过1
1 定义内部类，用于存储高度及该节点信息
class Info{
public boolean isBalanced;
public int height;
public Info(boolean isBalanced, int height){
this.isBalanced = isBalanced;
this.height = height;
}
}
2 定义递归函数，用于判断是否是二叉平衡树
public Info process(TreeNode node){
//如果当前节点为null，默认该节点为平衡的，且高度为0
if(node == null){
return new Info(true, 0);
}
//当前节点的左子树信息
Info leftInfo = process(node.left);
//当前节点的右子树信息
Info rightInfo = process(node.right);
//当前节点的高度信息：左右子树的最大高度 + 自身高度1
int height = Math.max(leftInfo.height, rightInfo.height) + 1;
//当前节点的isBalanced信息，取决于：左右子树是否平衡，同时左右子树的高度差是否小于2
boolean isBalanced = leftInfo.isBalanced && rightInfo.isBalanced &&
Math.abs(leftInfo.height - rightInfo.height) < 2;
//构建当前节点node信息
return new Info(isBalanced, height);
}
3 全部代码
class Solution {
public boolean isBalanced(TreeNode root) {
return process(root).isBalanced;
}
class Info{
public boolean isBalanced;
public int height;
public Info(boolean isBalanced, int height){
this.isBalanced = isBalanced;
this.height = height;
}
}
public Info process(TreeNode node){
if(node == null){
return new Info(true, 0);
}
Info leftInfo = process(node.left);
Info rightInfo = process(node.right);
int height = Math.max(leftInfo.height, rightInfo.height) + 1;
boolean isBalanced = leftInfo.isBalanced && rightInfo.isBalanced &&
Math.abs(leftInfo.height - rightInfo.height) < 2;
return new Info(isBalanced, height);
}
}
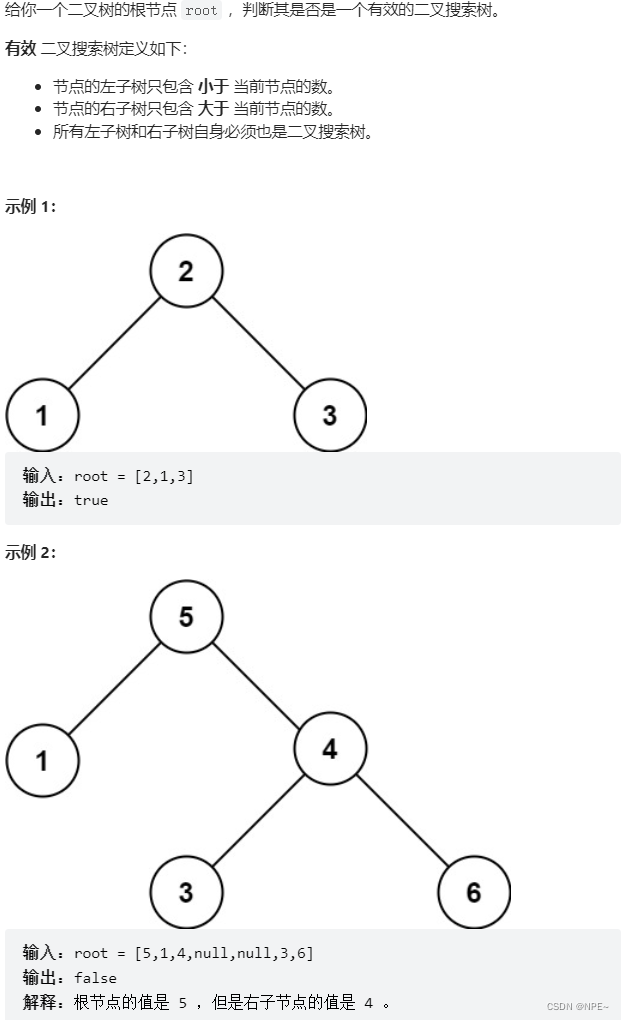
三、LeetCode - 098. 验证二叉搜索树
二插搜索树：根节点root的左节点的值小于根，右节点的值大于根
leftNode.val < root.val < rightNode.val
1 定义内部类Info存储子树的最大值，最小值，以及当前节点信息
public Info(boolean isBST, int min, int max){
this.isBST = isBST;
this.min = min;
this.max = max;
}
2 定义递归方法process，用于处理节点信息
public Info process(TreeNode node){
if(node == null){
//此处不能创建空的Info信息返回，因为如果创建空的返回，int默认是0，但是节点的值有可能是负数，会影响判断
return null;
}
Info leftInfo = process(node.left);
Info rightInfo = process(node.right);
int max = node.val;
int min = node.val;
//每次更新当前节点及其子节点的最大值与最小值
if(leftInfo != null){
max = Math.max(leftInfo.max, max);
min = Math.min(leftInfo.min, min);
}
if(rightInfo != null){
max = Math.max(rightInfo.max, max);
min = Math.min(rightInfo.min, min);
}
boolean isBST = true;
//当前左节点信息不为null，且不是搜索树
if(leftInfo != null && !leftInfo.isBST){
isBST = false;
}
if(rightInfo != null && !rightInfo.isBST){
isBST = false;
}
//判断左子树的最大值是否小于root的最小值
boolean leftMaxLessNode = leftInfo == null ? true : (leftInfo.max < node.val);
boolean rightMinMoreNode = rightInfo == null ? true : (rightInfo.min > node.val);
if(!leftMaxLessNode || !rightMinMoreNode){
isBST = false;
}
return new Info(isBST, min, max);
}
3 全部代码
/** * Definition for a binary tree node. * public class TreeNode { * int val; * TreeNode left; * TreeNode right; * TreeNode() {} * TreeNode(int val) { this.val = val; } * TreeNode(int val, TreeNode left, TreeNode right) { * this.val = val; * this.left = left; * this.right = right; * } * } */
class Solution {
public boolean isValidBST(TreeNode root) {
return process(root).isBST;
}
class Info{
public boolean isBST;
public int min;
public int max;
public Info(boolean isBST, int min, int max){
this.isBST = isBST;
this.min = min;
this.max = max;
}
}
public Info process(TreeNode node){
if(node == null){
//此处不能创建空的Info信息返回，因为如果创建空的返回，int默认是0，但是节点的值有可能是负数，会影响判断
return null;
}
Info leftInfo = process(node.left);
Info rightInfo = process(node.right);
int max = node.val;
int min = node.val;
//每次更新当前节点及其子节点的最大值与最小值
if(leftInfo != null){
max = Math.max(leftInfo.max, max);
min = Math.min(leftInfo.min, min);
}
if(rightInfo != null){
max = Math.max(rightInfo.max, max);
min = Math.min(rightInfo.min, min);
}
boolean isBST = true;
//当前左节点信息不为null，且不是搜索树
if(leftInfo != null && !leftInfo.isBST){
isBST = false;
}
if(rightInfo != null && !rightInfo.isBST){
isBST = false;
}
//判断左子树的最大值是否小于root的最小值
boolean leftMaxLessNode = leftInfo == null ? true : (leftInfo.max < node.val);
boolean rightMinMoreNode = rightInfo == null ? true : (rightInfo.min > node.val);
if(!leftMaxLessNode || !rightMinMoreNode){
isBST = false;
}
return new Info(isBST, min, max);
}
}
边栏推荐
猜你喜欢
随机推荐
401. Binary Watch
three.js简介
003_Kubernetes核心技术
【时间的比较】
我想请问下，我们的数据库是在亚马逊，Dataworks 连不通，怎么办？
广告电商系统开发之会员系统板块
Adobe是什么？
软件测试＜进阶篇--＞测试分类＞
图像传感第一章学习心得
【Metaverse系列一】元宇宙的奥秘
深度学习跟踪DLT (deep learning tracker)
Halcon 小笔记 C＃ 图片是否有效
【目标检测】Focal Loss for Dense Object Detection
CC2530_ZigBee+HUAWEI CLOUD IOT: Design your own cold chain acquisition system
融云「音视频架构实践」技术专场【内含完整PPT】
基于DMS的数仓智能运维服务，知多少？
FinClip | July 2022 Product Highlights
fastposter v2.9.0 程序员必备海报生成器
出海，是泡泡玛特的“解药”吗？
php之相似文章标题similar_text()函数使用