当前位置:网站首页>C#实现基于广度优先BFS求解无权图最短路径----完整程序展示
C#实现基于广度优先BFS求解无权图最短路径----完整程序展示
2022-07-01 02:58:00 【黄昏和星空】
本文介绍C#实现基于广度优先BFS求解无权图最短路径----完整程序展示
1、代码
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
namespace 图的应用__基于BFS算法求解的那元最短路径
{
using VertexType = System.Char;//顶点数据类型别名声明
using EdgeType = System.Int16;//带权图中边上权值的数据类型别名声明
class Program
{
public const int MAxVertexNum = 100;//顶点数目的最大值
public const int MAXSize = 100;
static void Main(string[] args)
{
MGraph G = new MGraph();
int u;
int[] d = new int[MAxVertexNum];
G.vexnum = 8;
G.arcnum = 8;
G.vex = new VertexType[MAxVertexNum];
G.Edge = new EdgeType[MAxVertexNum, MAxVertexNum];
for (int i = 0; i < MAxVertexNum; ++i)
{
for (int j = 0; j < MAxVertexNum; ++j)
{
G.Edge[i, j] = 0;
}
}
//图的赋值
G.vex[0] = ‘a’; G.vex[1] = ‘b’; G.vex[2] = ‘c’; G.vex[3] = ‘d’; G.vex[4] = ‘e’; G.vex[5] = ‘f’;
G.vex[6] = ‘g’; G.vex[7] = ‘h’;
G.Edge[0, 1] = 1; G.Edge[0, 2] = 1;
G.Edge[1, 0] = 1; G.Edge[1, 3] = 1; G.Edge[1, 4] = 1;
G.Edge[2, 0] = 1; G.Edge[2, 5] = 1; G.Edge[2, 6] = 1;
G.Edge[3, 1] = 1;
G.Edge[4, 1] = 1; G.Edge[4, 7] = 1;
G.Edge[5, 2] = 1;
G.Edge[6, 2] = 1;
G.Edge[7, 4] = 1;
//广度优先
Console.WriteLine(“广度优先:”);
BFSTraverse(G);
u = 3;
Console.WriteLine();
Console.WriteLine(“顶点”+G.vex[u]+“到各点最短路径:”);
BFS_MIN_Distance(G,u,ref d);
for (int i=0;i<G.vexnum;++i) {
Console.Write(d[i]+" ");
}
Console.Read();
}
/// <summary>
/// 图的定义--邻接矩阵
/// </summary>
public struct MGraph
{
public VertexType[] vex;//顶点表数组
public EdgeType[,] Edge;//临接矩阵、边表
public int vexnum, arcnum;//图的当前顶点数和弧数
}
/// <summary>
/// 图的定义--邻接表法
/// </summary>
public class ArcNode
{//边表节点
public int adjvex;
public ArcNode next;
}
public class VNode
{ //顶点表节点
VertexType data;//顶点信息
ArcNode first;//只想第一条依附改顶点的弧的指针
}
public class ALGraph
{
VNode[] vertices; //邻接表
int vexnum, arcnum;//图的顶点数和弧数
}
/// <summary>
/// 对图G的广度优先遍历
/// </summary>
static void BFSTraverse(MGraph G)
{
bool[] visited = new bool[MAxVertexNum];//访问标记数组
for (int i = 0; i < G.vexnum; ++i)
visited[i] = false;//访问标记数组初始化
SqQueue Q = new SqQueue();
Q.data = new int[MAxVertexNum];//需要对队列数组进行new
InitQueue(ref Q);//队列初始化
for (int i = 0; i < G.vexnum; ++i)
{
if (!visited[i])
BFS(G, i, ref visited, ref Q);
}
}
static void BFS(MGraph G, int v, ref bool[] visited, ref SqQueue Q)
{
visit(G, v);//首先访问初始顶点v
visited[v] = true;//对v做已访问标记
EnQueue(ref Q, v);//顶点v入队列
while (!isEmpty(Q))
{
DeQueue(ref Q, ref v);//顶点v出队列
for (int w = FirstNeighbor(G, v); w >= 0; w = NextNeighbor(G, v, w))
{
if (!visited[w])
{
visit(G, w); //访问顶点w
visited[w] = true;//对w做已访问标记
EnQueue(ref Q, w);
}
}
}
}
//控制台打印遍历点
static void visit(MGraph G, int v)
{
Console.Write(G.vex[v] + " ");
}
//查找G中,V顶点的首个邻接点
static int FirstNeighbor(MGraph G, int v)
{
int b = -1;
for (int i = 0; i < G.vexnum; ++i)
{
if (G.Edge[v, i] == 1)
{
b = i;
break;
};
}
return b;//返回首个邻接点
}
//查找G中,V顶点的W邻节点后的下一个邻接点
static int NextNeighbor(MGraph G, int v, int w)
{
int b = -1;
for (int i = w + 1; i < G.vexnum; ++i)
{
if (G.Edge[v, i] == 1)
{
b = i;
break;
};
}
return b;//返回下一个邻接点
}
//求单源最短路径,即u到各顶点的最短路径长度
static void BFS_MIN_Distance(MGraph G,int u,ref int[] d) {
bool[] visited = new bool[MAxVertexNum];//访问标记数组
SqQueue Q = new SqQueue();
InitQueue(ref Q);
Q.data = new int[MAxVertexNum];
for (int i=0;i<G.vexnum;++i) {
visited[i] = false;
d[i] = -1;//初始化路径长度。-1表示没有
}
visited[u] = true;d[u] = 0;
EnQueue(ref Q,u);
while (!isEmpty(Q)) {
DeQueue(ref Q, ref u);
for (int w=FirstNeighbor(G,u);w>=0;w=NextNeighbor(G,u,w)) {
if (!visited[w]) {
d[w] = d[u] + 1;
visited[w] = true;
EnQueue(ref Q, w);
}
}
}
}
/// <summary>
/// 队列结构体定义
/// </summary>
public struct SqQueue
{
public int[] data;//队列存放的元素
public int front, real;//队头和队尾指针
}
/// <summary>
/// 队列初始化
/// </summary>
/// <param name="Q"></param>
static void InitQueue(ref SqQueue Q)
{
Q.real = Q.front = 0;
}
/// <summary>
/// 判断队列是否为空
/// </summary>
/// <param name="Q"></param>
/// <returns></returns>
static bool isEmpty(SqQueue Q)
{
if (Q.front == Q.real) { return true; }
else return false;
}
/// <summary>
/// 入队
/// </summary>
/// <param name="Q"></param>
/// <param name="x"></param>
/// <returns></returns>
static bool EnQueue(ref SqQueue Q, int x)
{
if ((Q.real + 1) % MAXSize == Q.front) { return false; }
Q.data[Q.real] = x;
Q.real = (Q.real + 1) % MAXSize;
return true;
}
static bool DeQueue(ref SqQueue Q, ref int x)
{
if (Q.real == Q.front) { return false; }
x = Q.data[Q.front];
Q.front = (Q.front + 1) % MAXSize;
return true;
}
}
}
2、测试结果

边栏推荐
- An article explaining the publisher subscriber model and the observer model
- Introduction to kubernetes resource objects and common commands (II)
- [applet project development -- JD mall] uni app commodity classification page (first)
- Metadata in NFT
- 最好用的信任关系自动化脚本(shell)
- [linear DP] longest common subsequence
- PCB defect detection based on OpenCV and image subtraction
- Introduction to core functions of webrtc -- an article on understanding SDP PlanB unifiedplan (migrating from PlanB to unifiedplan)
- Chapter 03_ User and authority management
- VMware vSphere 6.7 virtualization cloud management 12. Vcsa6.7 update vCenter server license
猜你喜欢

Xception learning notes

实战 ELK 优雅管理服务器日志

【机器学习】向量化计算 -- 机器学习路上必经路

Multithreaded printing

Dell server restart Idrac method

POI exports excel and displays hierarchically according to parent-child nodes

8 pits of redis distributed lock
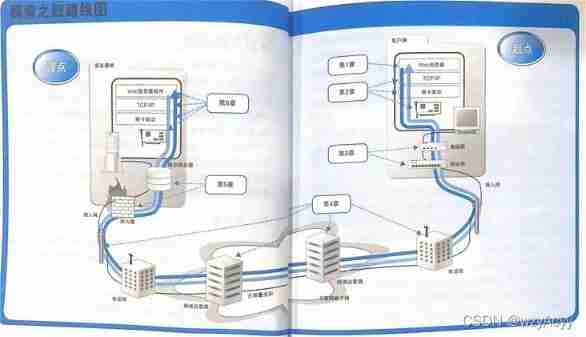
How the network is connected: Chapter 2 (Part 2) packet receiving and sending operations between IP and Ethernet

【小程序项目开发-- 京东商城】uni-app之分类导航区域

POI导出excel,按照父子节点进行分级显示
随机推荐
第03章_用戶與權限管理
Cloud native annual technology inventory is released! Ride the wind and waves at the right time
Use ipmitool to configure BMC network and user information of X86 server
最新接口自动化面试题
Prototype and prototype chain in JS
[QT] add knowledge supplement of third-party database
The best learning method in the world: Feynman learning method
实战 ELK 优雅管理服务器日志
MySQL index --01--- design principle of index
EtherCAT简介
Magnetic manometer and measurement of foreign coins
【日常训练】1175. 质数排列
Add / delete / modify query summary insert/create/put/add/save/post, delete/drop/remove, update/modify/change, select/get/list/find
大橙子疯博客搬家通知
How the network is connected: Chapter 2 (Part 2) packet receiving and sending operations between IP and Ethernet
js 找出两个数组中的重复元素
【小程序项目开发--京东商城】uni-app之自定义搜索组件(上)
Mouse over effect I
Introduction to kubernetes resource objects and common commands (II)
Scale SVG to container without mask / crop